
Бесплатный фрагмент - Gold trader
The Relationship Between Even Powers of the Gaussian Integral, the Gamma Function, and Fibonacci Levels
Even powers of the Gauss integral connection with the gamma function
The relationship between even powers of the Gauss integral and the gamma function is expressed as follows:
Let us consider an integral of the form
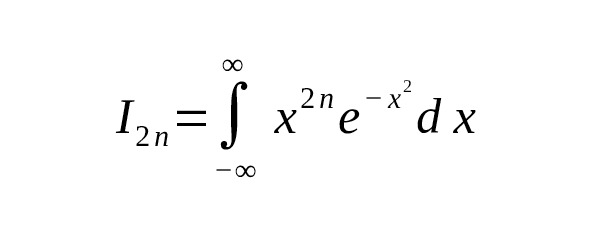
where is an even degree.
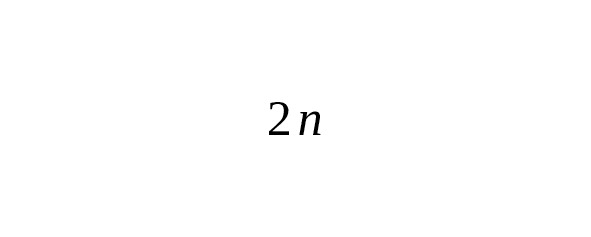
This integral is expressed in terms of the gamma function as follows:
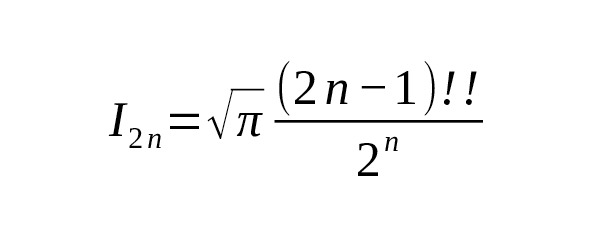
or, using the properties of the gamma function:
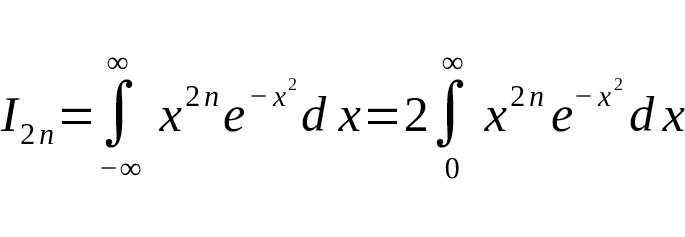
Replacing the variable $ t = x^2 $ leads to the gamma function:
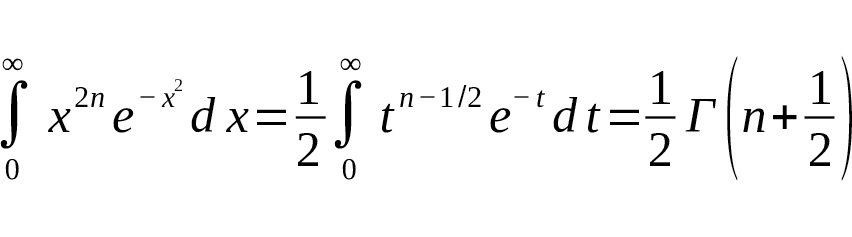
Thus,
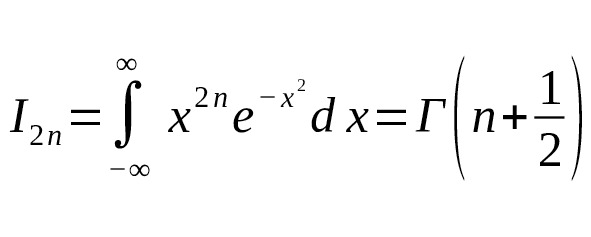
— Even moments of the Gaussian integral are expressed through the gamma function of a half-integer argument.
— For the general case: where for standard Gauss $ m=2n,,a=1,,b=2 $ [1] [2].
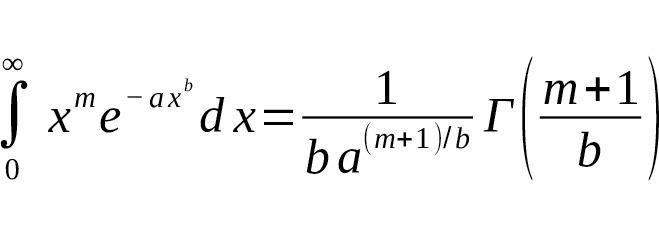
This shows the direct connection between even powers of the Gauss integral and the values of the gamma function, and explains why the values for half-integer arguments are expressed in terms of $ \sqrt {\pi} $ [1] [2].
— For example, for $ n=0 $ (that is, the standard Gauss integral):
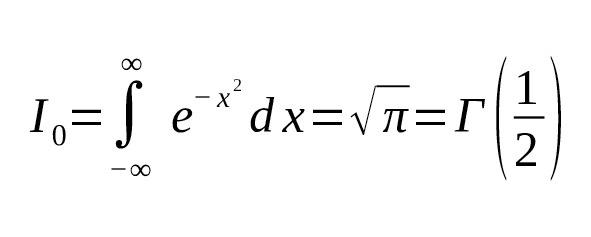
— For $ n=1 $:
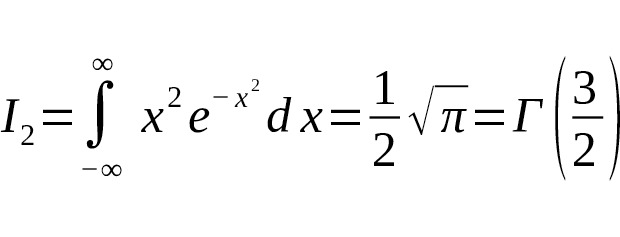
That is, the values of even Gaussian moment integrals are directly expressed through the gamma function for half-integer arguments [1] [2].
Examples of use :

⁂
List the literature on this topic
The main sources on the topic of Gauss integrals with even powers and related topics of quadratures, calculations and applications are:
— Fichtenholz G.M. «Course of Differential and Integral Calculus», v.2. Classic textbook, examines in detail Gaussian integrals, their properties and calculations [3].
— Kraynov V.A. «Numerical Methods for Calculating a Definite Integral». The manual examines methods for exact and approximate calculation of integrals, including Gaussian integrals, discusses accuracy for even-degree polynomials, and provides formulas [4].
— Fedotov AA «Numerical methods of integration». Modern manual with practical examples of numerical calculation of Gaussian integrals and their applications [5].
— Pastukhov D.F. «Gauss quadratures. Integral equations». Methodical instructions for the construction and application of Gauss quadrature formulas for calculating integrals of polynomials even of high degree [6].
— Dobrynina S.V. «Quadrature and cubature formulas». The manual contains practical tasks and analysis of the rules of approximate integration, including Gauss’s formulas for integrals with weights and polynomials [7].
— Arushanyan I.O. «Algorithms for approximate calculation of integrals». Methods for calculating integrals with various degrees of accuracy are discussed, including the use of even powers in Gaussian integrals [8].
These books and manuals are suitable for an in-depth study of the calculation and theory of Gaussian integrals, their properties and applications.
⁂
Theoretical foundations of quadrature formulas
Quadrature formulas are a classic mathematical tool for the approximate calculation of definite integrals over function values at a finite number of points. Their main purpose is to replace the calculation of the integral with a sum, where the coefficients and choice points (nodes) are selected to achieve maximum accuracy on a certain class of functions [9] [10] [11].
General form of the quadrature formula
Any quadrature formula usually has the following form:
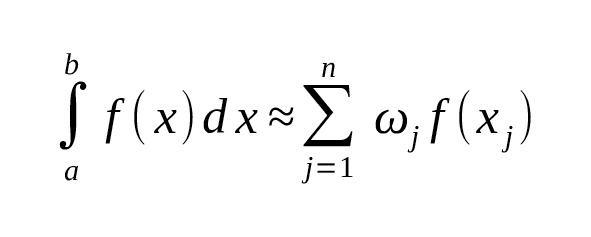
Where:
— — formula nodes (points at which the function is calculated),
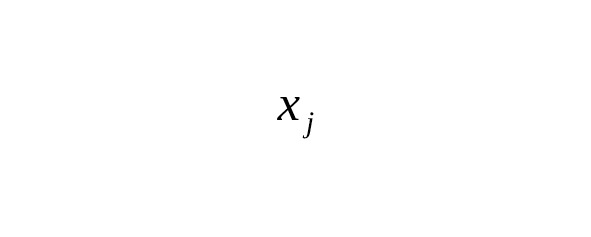
— — weights (coefficients with which the function value at the nodes is taken).
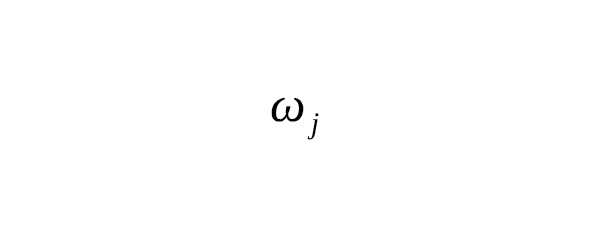
Theoretical Provisions
— The accuracy of a quadrature formula is determined by the class of functions for which the formula gives the exact value of the integral. Usually these are polynomials of degree no higher than a certain value.
— The error (remainder term) of the quadrature formula shows how accurately the integral is approximated [10] [12].
— Selection of nodes and weights: For example, in the Newton–Cotes formulas, the nodes are equidistant, while in the Gauss formulas, they are the roots of orthogonal polynomials (for example, Legendre polynomials for the classical integral on a segment), which allows achieving the highest algebraic degree of accuracy — for nodes [11].
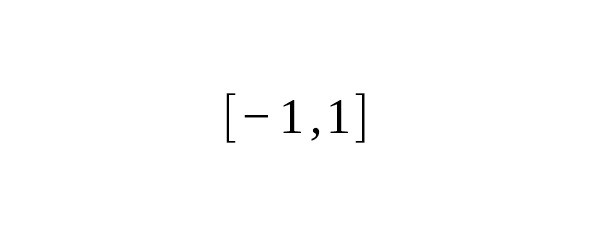
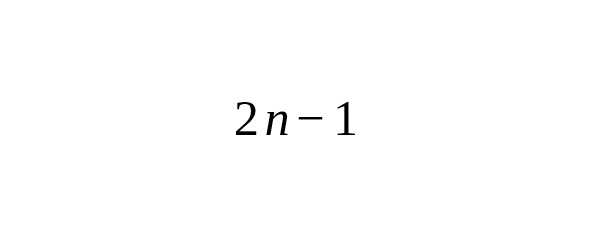
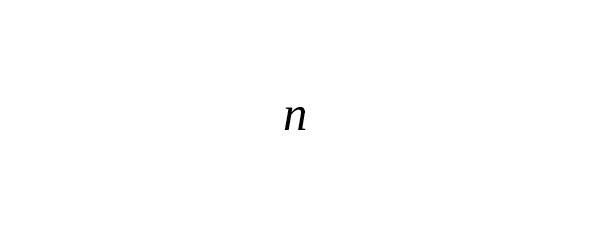
— Historical background: methods of approximate integration arose in the times of Newton and Leibniz. The construction of classical formulas (rectangles, trapezoids, Simpson) is based on replacing the function inside the segment with some simple approximation (polynomial) and integrating this approximation [10].
Types of quadrature formulas
— Interpolation quadrature formulas: are based on the interpolation of a function (usually a polynomial one) [11].
— Compound (interval partitioning): a long interval is divided into parts, and a simple formula (such as the trapezoid or Simpson compound formula) is applied to each part [12] [11].
— Weighted quadrature formulas are used when the integrand contains singularities (e.g., singularities or rapid growth) [10] [13].
Error and degree of accuracy
— The degree of accuracy is the highest degree of a polynomial for which the formula gives an exact integral.
— The error is estimated through the upper bound of the high-order derivatives of the integrand (usually the Taylor residue formula) [11] [10] [9].
Examples
— Rectangles:
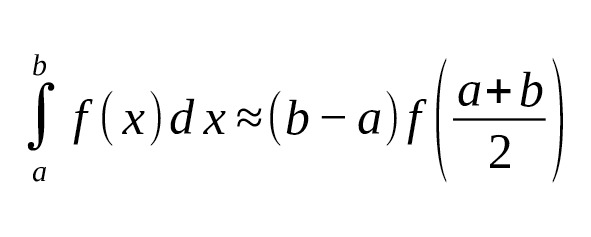
— Trapezius:
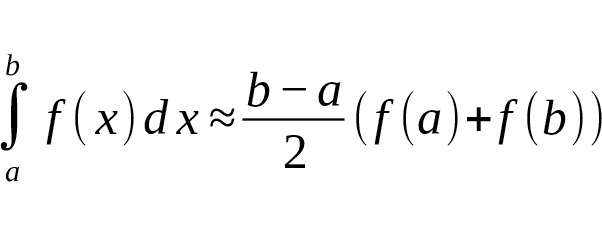
— Simpson: exact for polynomials up to degree [9] [12]
Summary
A quadrature formula is the result of a strictly mathematical construction in which the choice of nodes and weights results in a compromise between accuracy and computational simplicity. The entire theory of quadrature formulas is reduced to the problem of optimally approximating an integral by a summation function with the highest possible accuracy at minimum computational costs [11] [10] [9].
⁂
The Gauss integral is equal to the Gamma function
The relationship between the Gauss integral and the gamma function is expressed through integrals of powers of $ x $ with an exponential function and a change of variables. The classical Gauss integral looks like this:
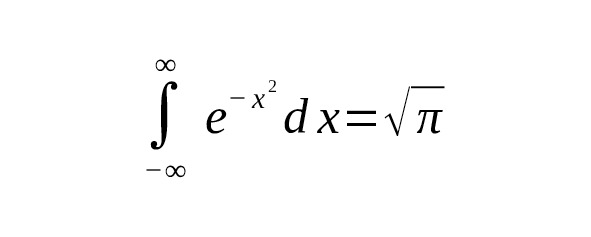
The gamma function by definition is:
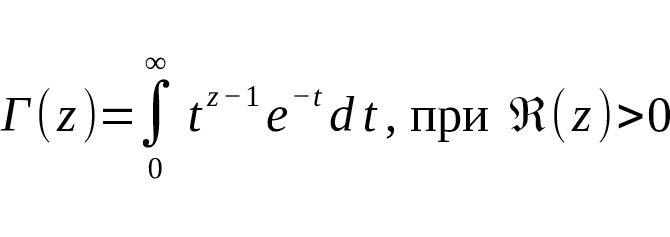
[14] [15] [16]
For certain values of the argument, this function calculates integrals that are very close in form to Gaussian integrals. For example, for integrals of the form:
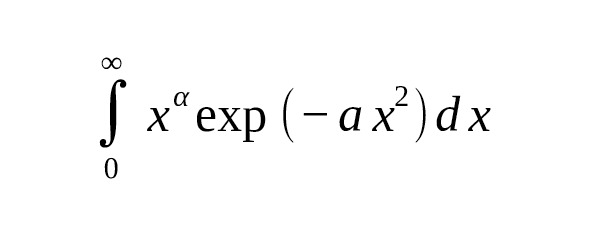
the expression can be written using the gamma function:
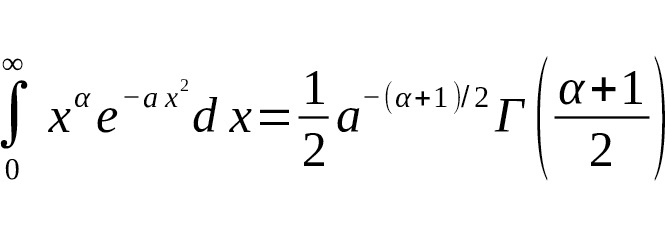
This means that the «Gaussian» type integrals with even and odd powers of $x$ are directly related to the gamma function of a half-integer (fractional) argument [14] [17].
The Gaussian integral is a special case of this expression for and. Then
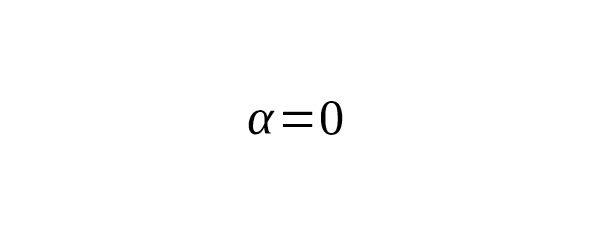
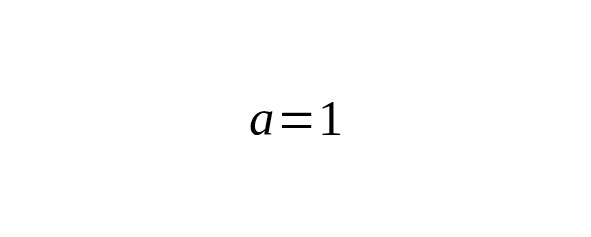
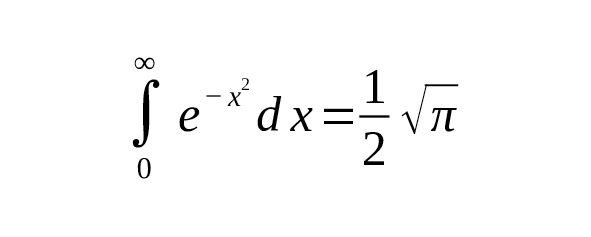
or, what is the same:
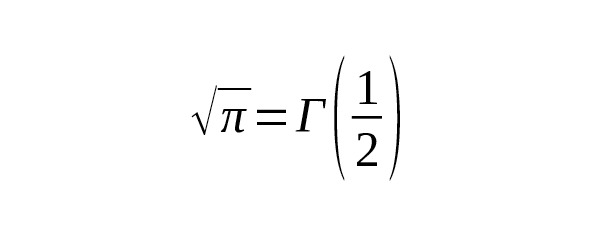
That is, [14] [17].
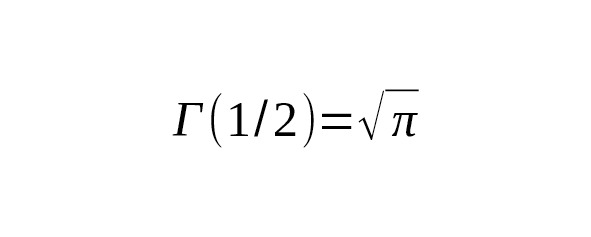
So:
— The Gauss integral is expressed in terms of the values of the gamma function, especially in the case of non-integer (usually half-integer) arguments.
— A more general formula relates integrals of the form with and parameter [14] [17].
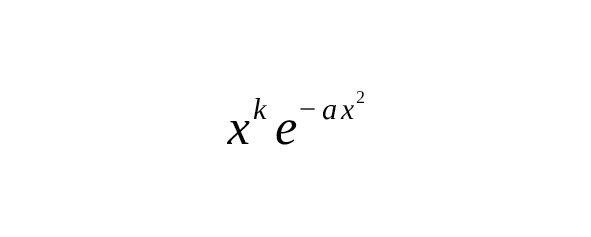
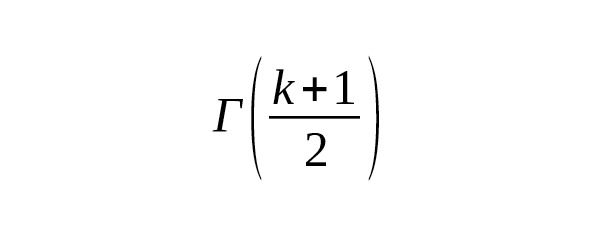

These connections are actively used for calculations in probability theory, physics and mathematics.
⁂
The relationship between the Gauss integral and the gamma function
The connection between the Gauss integral and the gamma function is evident in the calculation of integrals of the form $ \int_0^ {\infty} x^ {\alpha} e^ {-ax^2} dx $, which can be expressed directly in terms of the gamma function with a half-integer argument:
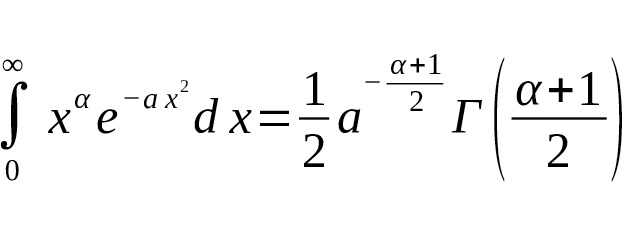
Here $ a> 0 $, $ \alpha> -1 $, and $ \Gamma (z) $ is the gamma function.
Classical Gauss integral:
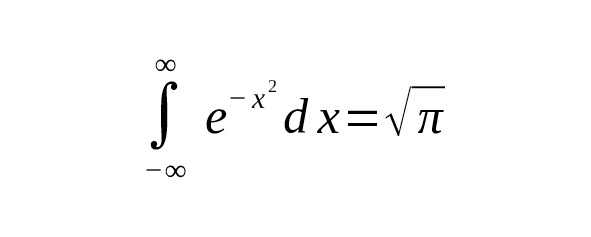
is a special case when and, but taken along the entire axis. For the half-interval:
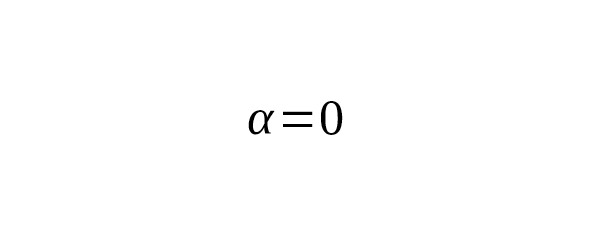
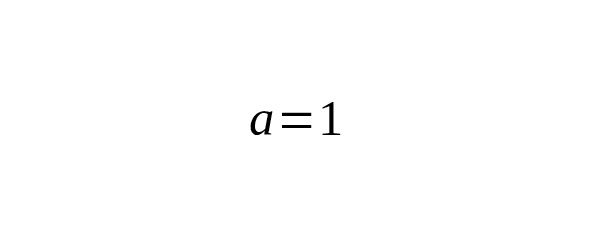
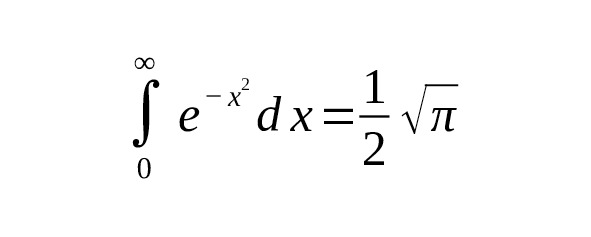
which is consistent with the fact that.
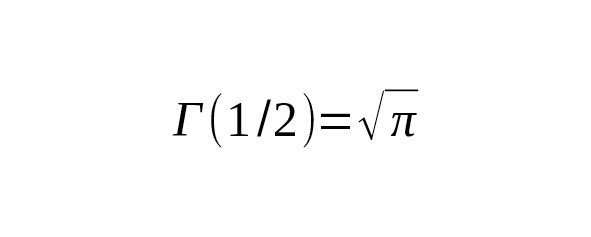
Thus:
— All integrals of the form are expressed through the -function with argument.
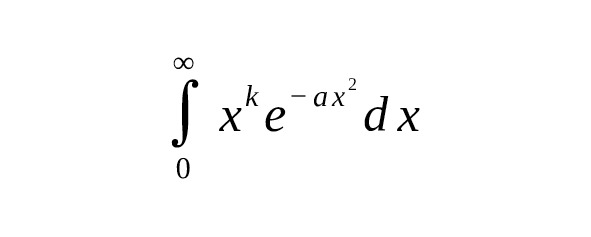
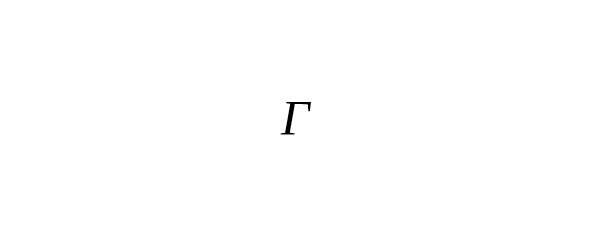
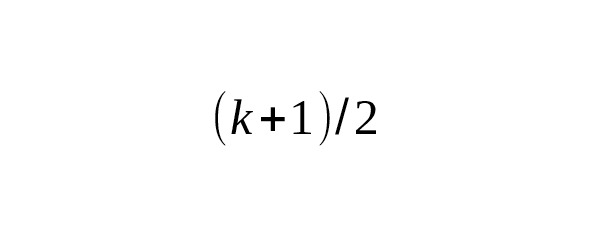
— The value of the Gaussian integral is nothing more than the definition of the gamma function.
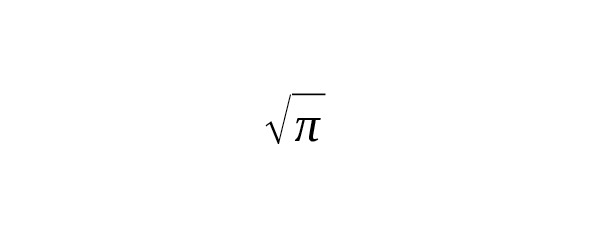
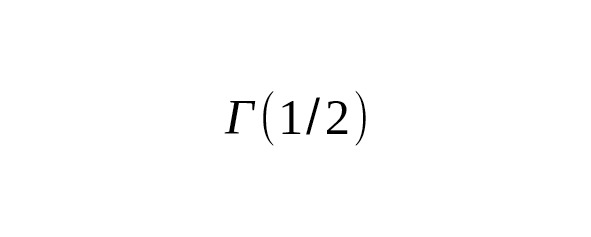
This connection allows one to calculate the so-called moments of the normal distribution and to use the results for analytical and numerical problems in mathematics, statistics and physics.
Analyze these equations
The figure shows important integrals associated with the Gaussian function $ e {-x 2} $ and its powers, as well as their analytical expressions.
Analysis of Equalities
— Type of integrals
Most integrals have the following form (for the entire axis or half-axis):
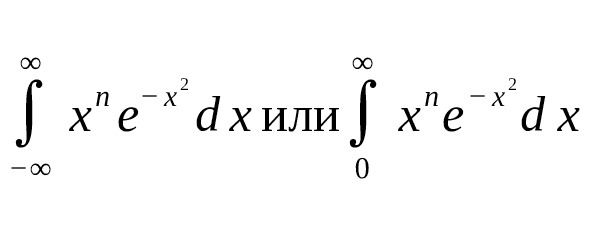
where $ n $ is a non-negative integer.
— Odd degrees
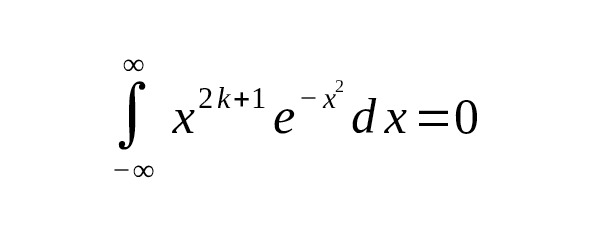
This is true because the function is odd: even powers are even, odd powers are odd, and $ e {-x 2} $ is even. The integral of an odd function on a symmetric interval is zero.
— Even powers
Integrals of even powers form a non-empty sequence:
— For $ n=0 $:
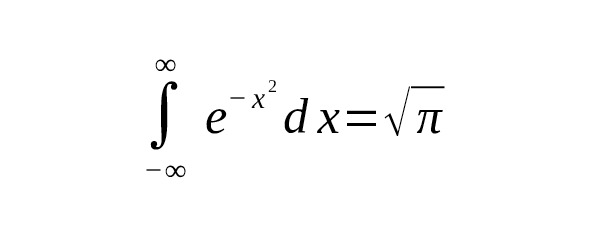
— For $ n=2 $:
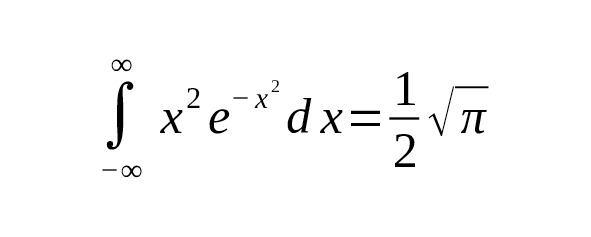
— For $ n=4 $:
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.