Бесплатный фрагмент - Многообразие тригонометрии. часть 1

---

Автор произведения и данной теории Ю. Н. Хахалкин

---

Многообразие тригонометрии

Трактат по

теории дерадианных дробей

Предисловие от автора теории дерадианных дробей

…Было бы легче остановить Солнце, легче было сдвинуть Землю, чем уменьшить сумму углов в треугольнике, свести параллели к схождению и раздвинуть перпендикуляры к прямой на расхождение. (В. Ф. Каган)

Только с алгеброй начинается строгое математическое учение. (Н. И. Лобачевский)

Лучший способ изучить что-либо — это открыть самому.

(Д. Пойа)

Я приветствую всех любителей математики, всем доброго времени суток! Всем, кто любит что-то посчитать, чертить, измерять. В этой книге я хочу показать читателю новый способ подхода к новому осмыслению и пониманию угла в геометрии и тригонометрии, попробовать посмотреть на это фундаментальное понятие немного в другом ракурсе, непривычном для обычного человека, в ракурсе, дополняющем стандартное евклидово понимание угла и все, что что с ним связано в обычной школьной математике, геометрии, тригонометрии, планиметрии. Тем более что до меня никто еще такого не делал, не рассматривал понятие угла в таком новом ракурсе, возможно, я первый, кто так подошел к этому вопросу (вернее, рассматривали, как выяснилось мной намного позже, но совершенно в другой области и в чисто прикладной задаче, и ни о какой строгой математической дисциплине отдельно и речи не шло, о чем я, конечно, ничего не знал, но это нисколько не умаляет моей теории дерадианных дробей и всего, что из нее проистекает в дальнейшем, так как я к ней пришел самостоятельно, из собственных размышлений), тем, я думаю, и интересней будет эта книга для неискушенного читателя. Это лишь мой способ решения задач по геометрии, тригонометрии, который я наработал еще будучи студентом и абитуриентом, учась в училище, и спустя столько лет наконец-то решился написать об этих моих наработках для других интересующихся математикой людей и тебя, мой дорогой читатель, и показать, что в мире математики еще столько есть не изученного до сих пор, хоть нам и кажется порой, что мы ушли в понимании ее очень далеко. Но стоит копнуть даже в самых истоках ее чуть поглубже, и на свет появляются новые теории, переворачивающие обычное представление об обычных вещах, которые так давно нам знакомы, со школьной скамьи, что казалось настолько незыблемым и фундаментальным, к чему уже никакие, казалось бы, знания уже не приложишь и не отнимешь, но если посмотреть на эти же вещи под другим углом, то сразу открываются нам новые свойства и аспекты бытия.

Что подвигло меня написать эту книгу? Во-первых, то, что я нигде никогда ничего подобного не слышал и не читал (оказывается, я случайно наткнулся и нашел аналог похожего понятия, но об этом позже), возможно, это и есть уже в науке, но мне не встречалось. Во-вторых, это то, что с раннего детства, занимаясь математикой, я всегда пытался понять и открыть что-то новое для себя, никогда не переставал поражаться и удивляться красоте и логичности математических законов и теорий, и в один прекрасный день, еще будучи молодым студентом училища, когда я изучал тригонометрию, я начал задумываться, почему тригонометрия на сегодняшний день такая незавершенная и «несовершенная». Да, в ней многое есть — теорема синусов, теорема косинусов, тригонометрические функции, — но все же чего-то мне все время не хватало. Я стал задаваться вопросами, почему на сегодняшний день мы так мало знаем типов углов, в основном 30°, 45°, 60°, 90°, а также другие, да и на практике в основном только их и применяем, но этого мало для расчетов. Или другие вопросы, почему,

например, Sin (π/6) =1/2 существует в наших школьных тригонометрических таблицах, а выражения для тангенса, равного, например, одной второй:

Tan (x) =1/2, x=?

нет, хотя, по идее, он также должен отображаться в таблицах? Или еще другие примеры, например:

Sin (π/4) = √2/2, Cos (π/4) = √2/2

Sin (π/3) = √3/2, Cos (π/6) = √3/2

Sin (π/2) =1, Cos (0) =1

А вот чему равны углы для соответствующих углов тангенсов, таблично никак не выражается, и это немного для меня всегда было странным, однако найти эти значения теперь не составляет особого труда в связи с появлением и наработками моей теории дерадианных дробей, теперь это сделать несложно, и эти углы будут равны:

Tan (x) =1/2, x ≡ (1 & 2)

Tan (x) = √2/2, x ≡ (2√2 & 2+ √6)

Tan (x) = √3/2, x ≡ (2√3 & 2+ √7)

Tan (x) = 1, x ≡ (2 & 1+ √2) и т. д.

Также меня волновали и другие вопросы, например, решая задачи тригонометрии, задачи на окружности и при вычислении обратных тригонометрических функций и многих других, я заметил, что выражения типа:

2Tan (α/2), 2Sin (α/2)

√ (4H2+A2), 2ArcTan (a/b),

Или вот еще мое интересное выражение:

ArcTan [1/2] = 2ArcTan [2 φ-1], φ-золотое сечение и т. д. очень часто встречается в этих задачах. Почему вся тригонометрия основана только на числе Пи, а не на каких-то иных константах? Их, наверное, должно быть на самом деле больше. А что если все это из-за единственности представления нами самого числа Пи? Просто, кроме него, ничего не предлагаем другого. А что, если вместо числа Пи ввести другие константы? Возможно, тригонометрий или «подтригонометрий» станет множество, для каждой универсальной константы будет своя тригонометрия. И я даже ввел одну такую константу и назвал ее γ-гамма. Выглядит она так:

γ = π/ (2ArcTan (1/2)) =3,3879…

А угол, соответствующий ей в градусах, назвал один дерадиан 1d: (1 & 1) ≡ 180°/ γ =53,1301…°=1d=1 дерадиан.

Собственно, от этой величины и началась когда-то моя новая теория. Хочу сказать, что для этой новой константы также существуют таблицы синусов, косинусов, тангенсов и т. д., все то же самое, что и для обычной универсальной константы числа Пи, разница лишь в том, какую константу мы берем за базис, все в этом мире относительно. Если бы мы, например, никогда не знали ничего о числе Пи, то мы могли бы точно так же находить длину окружности, площадь круга и т. д., но теперь только уже не через число Пи, а через новую универсальную постоянную — число Гамма, и только угловые меры бы уже выражались не радианами, как мы привыкли, а дерадианами. Также в этой новой тригонометрии сумма углов в треугольнике уже бы равнялась не числу Пи радиан, это точно пол-оборота на тригонометрической окружности, а числу Гамма, только уже дерадиан, так же равному половине оборота на тригонометрической окружности, и так же отношение длины дуги к диаметру было бы уже опять не число Пи, а число Гамма и т. д. В этой новой тригонометрии сохраняются все законы обычной классической тригонометрии, например:

30°⁓ (π/6) r ⁓ (γ/6) d

45°⁓ (π/4) r ⁓ (γ/4) d

90°⁓ (π/2) r ⁓ (γ/2) d

r — в радианах, d — в дерадианах.

И таких констант можно ввести превеликое множество, по аналогии с константой Гамма. И, кто знает, возможно, этих новых констант конечное число, а не бесконечное, ну или по крайней мере счетное множество. Возможно, даже существует какая-то сводная таблица таких констант, мировой закон тригонометрических констант, ну или что-то в этом духе. Но это уже, как мне видится, немного из фантазии или, возможно, наука будущего. И вообще я долго колебался написать данную книгу, пока наконец-то не решился окончательно. Все думал, и казалось, что это все несерьезно для теории, кому это интересно, а вдруг не поймут, а вдруг засмеют, раскритикуют и т. д. Как хорошая идея — да, но как теория, думал, слишком несерьезна, но, несмотря на все свои колебания, вдруг все-таки решился написать сию книгу. Ладно, думаю, может, эта идея или теория и вправду кого-то заинтересует и подтолкнет к последующим шагам и великим открытиям, тогда для таких людей и стоит написать эту книгу. Также, учитывая все это и задавая себе эти и другие вопросы, я пришел к выводу, что нам просто не хватает понятной величины для выражения в удобном виде угла, чтобы с этой величиной удобно было работать и обозначать ее как-то стандартно и желательно в целых числах, и решил изобрести такое новое обозначение, и назвал это обозначение «дерадианная дробь». Для меня это новое понятие и в математике с конструкцией, с которой я еще никогда не сталкивался и нигде не встречал (оказывается, похожее понятие уже существует в дисциплине «инженерная графика», и это понятие «К-Конусность», о котором я узнал после написании уже 70% книги), и эта конструкция дерадианного угла частично сняла некоторые мои вопросы, но, как обычно бывает, добавила новых, еще более запутанных и непонятных. Например, все мы знаем тригонометрическую окружность с ее стандартным делением на части:

{0, 2π, π, π/2, π/3, π/4…} °

и т. д., и почему наша окружность непременно при решении задач должна делиться на такие части, умножая которые на какой-то n, n∈ℚ, обязательно получим полную окружность? Может, пора нашу окружность поделить на какие-то иные части, не столь пропорциональные полной окружности? В каждой конкретной задаче, возможно, нужна своя измерительная система угла Gn, не связанная с числом Пи, ведь числовая окружность (мое понятие — аналог понятия числовой прямой) на самом деле бесконечна и не ограничивается одной только угловой измерительной системой. Иначе мы всю геометрию должны замкнуть в парадигме числа Пи и при этом никак не развиваться дальше в изучении глубины и новых свойств пространства, а ведь на самом деле углы тоже имеют свою внутреннюю математическую природу и множественную структуру, например, прямой угол — 90° — это не то же самое, что угол 53,1301…°. Как станет ясно в дальнейшем из этой книги, оказывается, существуют углы разной природы. Как мы отличаем на числовой прямой множество всех целых чисел от множества рациональных и иррациональных точек, то же самое, как мне видится, существует и на числовой окружности. В основном об этом всем и пойдет речь в этой книге.

И казалось бы, зачем нам еще одна новая константа Гамма, которая к тому же еще и находится через число Пи? Зачем изобретать велосипед еще раз, когда его уже давно изобрели другие? А оказывается, что углы в тригонометрии этой константы мы можем записывать как целые или дробные значения, ну или как алгебраические, в то время как в тригонометрии постоянной числа Пи они трансцендентны и не очень понятные на письме величины, а это бывает не совсем удобно при письме и усложняет понимание при решении задач. Возможно, отсюда и родилась у меня такая странная мысль так странно назвать свою книгу — «Многообразие тригонометрии, или Теория дерадианных дробей», что значит много образов тригонометрий, построенных на записи дерадианных дробей и множества констант. Возможно, кого-то заинтересует это новшество и этот человек сможет развить, переработать, почерпнуть что-то для себя новое и понести дальше эту идею, тем более что, занимаясь этой теорией, я все больше и больше убеждаюсь, что нет, наверное, области в математике, которую бы эта теория не пронизывала и не затрагивала так или иначе, и во многих областях математики я вижу отражение или присутствие ее идей, пусть она и выглядит немного притянуто и наивно, но возможно, что-то в этом и окажется правдой в будущем.

Также вторая идея, которая меня осенила или озарила, — глядя на пирамиды Египта, я удивлялся все время, как, не зная синусов, косинусов и современной тригонометрии, древние египтяне построили такие стройные и большие сооружения с такой точностью. Значит, они обладали какой-то иной тригонометрией, которая позволяла им обходить вычисления тригонометрических функций, и, возможно, я нашел гипотетически, какой они могли пользоваться тригонометрией, а именно тригонометрией с использованием дерадианных дробей — это тригонометрия, которая все считает в целых числах и дробях и для которой тригонометрические функции — это лишь дроби, которые зависят только от апофемы и высоты угла, а также от гипотенузы. Вот поэтому в этой книге я и хочу познакомить читателя с этой новой, еще, видимо, никому не известной тригонометрической теорией, которую мне пришлось придумать самому от самого начала. А уже читатель будет сам решать, что здесь вымысел, а что правда.

Эта книга будет изложена простым математическим языком, известным еще со школьных лет, которому нас учили в школе, и знаний каких-то сложных абстракций не потребует. Конечно, эта моя теория не закончена, и ее еще можно развивать и углублять дальше и шире, и это может сделать любой желающий, и, возможно, ты тот человек, кто разовьет и понесет дальше эту идею для потомков и всего человечества. Я в этой книге хочу лишь заложить фундамент для нового осмысления старых истин, прошу не судить меня строго, если где-то что-то я изложу не совсем так, как требует этого фундаментальная наука (например, где-то совсем очевидные высказывания не стану строго доказывать или в терминах или обозначениях буду не совсем строг, но из контекста будет понятно, о чем идет речь). Также постараюсь не углубляться в дебри абстракций, и все, что будет написано в этой книге, по уровню понимания не будет превышать знаний 9—10 класса, но все же постараюсь соответствовать ей настолько, насколько хватит мне умения и знаний, ведь я не профессиональный математик, а всего лишь скромный любитель математики. Все доказательства буду стараться приводить чисто геометрически, избегая по возможности каких-то сложных строго аксиоматических подходов теории множеств, но иногда без этого просто будет не обойтись. Также, так как эта дисциплина нова в тригонометрии и в целом в математике, могу в чем-то и ошибаться, но время все расставит по своим местам: или откинет эти мои рассуждения, или они станут еще одним из разделов математики. Я, если честно, даже еще толком не знаю, к какому разделу или дисциплине математики отнести эту теорию, настолько уж она похожа и не похожа одновременно на некоторые другие разделы математики: у нее присутствуют признаки как геометрии, так и тригонометрии, и, возможно, что-то от планиметрии и от алгебры, и от теории множеств, и от линейной алгебры и т. д. Возможно, со временем она станет отдельным тригонометрическим классом знания. А пока для меня главное в этой книге — не писать все на заумном языке, а показать саму суть теории в общих чертах, заинтересовать читателя и показать, как эту теорию можно использовать на практике и применять в других научных дисциплинах. А строгость и научность оставим глубокоуважаемым нашим профессорам, они в этом больше понимают. Так как я не имею каких-то особых степеней и заслуг и также не обладаю особо большими знаниями в высшей математике — чуть выше среднего, буду все излагать с точки зрения, так сказать, математика-любителя, поэтому возможны какие-то огрехи, неточности в обозначениях и доказательствах, оговорки в терминах и т. д., но в общем это сути дела не меняет, главное — передать саму суть, мысль и соль идеи. Ну что, давайте тогда приступим! Удачи всем и терпения в понимании и в познании всего нового и забытого старого знания!

Хахалкин Ю. Н.

P. S. Все, что написано в этой книге, что касается дерадианной теории, ее идей и терминов, — сугубо моя личная разработка, опубликованная впервые. До меня никто ничего подобного не писал и не издавал. И сама элементарная теория дерадианных дробей — это моя сугубо личная теория, и всю ответственность за термины и идеи несу лично я. Прошу не судить меня строго и приношу свои извинения, если где-то что-то написано немного коряво, вычурно, нелепо и непонятно, а также, возможно, порой притянуто за уши и где-то даже наивно. Я думаю, в дальнейшем последующие математики этого поколения или следующего разберутся, принять или отвергнуть эту теорию, я лишь только выношу на ваш суд и рассмотрение свою идею в попытке внести новую и свежую струю мысли в современную тригонометрию.

P.P.S. Когда я написал уже более чем 70% книги и прошло два года после этого, я встретил наконец-то в «Википедии» статью под названием «Конусность», я был, конечно, очень удивлен такому простому и редкому понятию, так как ничего не знал об этом понятии, хоть и предполагал, что что-то похожее уже есть в жизни, пусть не прямо в самой математике, а в ее прямом приложении. Оказывается, похожее понятие уже было известно и до меня, о котором я, конечно же, ничего не знал, и, оказывается, это понятие в виде дроби применяют для измерения конусности деталей на чертежах, поэтому я всегда и говорю, что все новое — забытое старое. По сути, понятие «конусность» — это и есть тангенциальная дробь первого типа в моей теории, только применяется к трехмерной фигуре под названием «конус» или «усеченный конус», в отличие от меня, где я применяю похожее понятие «дерадианная дробь» к плоскому углу и даже ввожу новые понятия — «дерадианный угол» и «дерадианный треугольник» (двух других понятий — это второго типа (синусоидального) и третьего типа (косинусоидального) типа дерадианных дробей — я пока в аналогах технических понятий не встретил). Единственное, в этом понятии «конусность» дается две, возможно, три формулы максимум и таблицы дробей стандартов утвержденных конусов (можно ли назвать это теорией, не знаю), и на этом все, вся теория конусности заканчивается, возможно, кто-то где-то и считает эти дроби по какой-то теории, но ни о какой математической общей концепции или общедоступной теории я нигде и никогда не слышал, поэтому я это понятие «конусность» буду считать хорошим применением, приложением в качестве хорошего примера на практике чисто математической теории дерадианных дробей, которая совсем о другом — эта теория о чистой математике как она есть, например, так же как мы для операции дифференцирования находим отражение во многих прикладных задачах физики, таких как скорость, перемещение, ускорение в механике, астрономии и так далее, но это не отменяет того факта, что существует чисто математическая теория «Дифференциальное исчисление», и в этом случае я буду считать точно так же: есть прикладные понятия, а есть чисто абстрактные математические, без привязки к каким бы то ни было материальным предметам: втулка, подшипник, дом, скамейка, ракета и так далее. Так как я к этой теории пришел совершенно самостоятельно, еще будучи студентом, и руководствовался совершенно другими идеями, задачами и принципами чистой математики и геометрии, и ставил изначально другие задачи и вопросы для нее, и в целом такого понятия, как «конусность», мы в геометрии в школе не изучали и до сих пор никто не изучает, и это странно, потому что это, по сути, чисто математическое и геометрическое понятие, например, есть понятие, родственное понятию «конусность», — это понятие «уклон» — чисто техническое понятие, уклон трубы, уклон дорожного полотна, уклон пандуса и так далее, в математике этому понятию соответствует свое чисто математическое понятие «коэффициент угла наклона» или «тангенс угла наклона», но вот о понятие «конусность» впервые и случайно прочитал на «Википедии», и такое бывает в жизни. Поэтому прошу и с этой стороны не судить меня строго, возможно, в будущем еще откроется что-то такое, о чем я и близко понятия не имел, но оно до меня существовало, но в другом виде! Это проблема всех ученых и исследователей — а вдруг то, что ты исследуешь, уже известно, а ты просто об этом не знаешь, и это сильно подкашивает что-то исследовать! Меня, конечно, это не остановит от дальнейшего написания книги, и даже не столь важно, что уже что то было до меня открыто кем-то, а главное, что это мои мысли, придуманные мной от начала и до конца, и моя личная идея, которой я и хочу поделиться со всеми вами, по крайней мере, я в этой книге и последующей выражу все, что я хочу выразить, и донести все, что хочу донести до читателя, а вы уже, мой дорогой читатель, сами решите, что вам будет полезно, а что нет, что может пригодиться, а что нет, и что было до меня, а что останется после этой книги.

ВВЕДЕНИЕ

С давних времен человечеству было известно понятие угла, это произошло еще во времена Пифагора и Евклида, а возможно и раньше их, где-то витало в воздухе общее понимание, что такое абстрактное понятие «угол». По сути, вся современная математика и началась с геометрии. Во времена, когда геометрия заменяла алгебру, и с тех пор вот уже тысячелетия ничего нового не происходило с этим фундаментальным понятием «угол», разве только увеличивалась размерность в пространстве: плоский угол, двух- или трехмерный угол и далее, более многомерный, и, соответственно, все измерения, которые с ним проводились по одним и тем же неизменным правилам тригонометрии и геометрии посредством таких формул, как теорема синусов, теорема косинусов, основное тождество тригонометрии, и основных отношений в треугольнике противолежащих и прилежащих сторон, где главным объектом всегда выступал прямоугольный треугольник, через который производились все вычисления, и связанной с ним крепко теоремой Пифагора, но, возможно, настала пора что-то поменять в обычном ходе вычислений и выбрать иной базис измерений, а именно: заменить базис «прямоугольный треугольник» на базис «равнобедренный треугольник» как бы взять калибр побольше, который, так или иначе, все равно в конечном счете основан на прямоугольном треугольнике, но, возможно, такой новый подход откроет какие-то новые грани в процессе вычислений и высветит новые аспекты пространственной природы. Что я и попытался сделать в данной книге. Данный подход не умаляет и не отбрасывает методы «обычной» тригонометрии, а берет на вооружение все, что в ней есть лучшее, и применяет в своих сугубо внутренних целях для нахождения тех или иных аспектов величин, таких как апофема, высота, гипотенуза, и лишь касающихся только самой теории дерадианных дробей, или «дерадианной тригонометрии», можно ли назвать новый подход самостоятельной тригонометрией или нет, в этой книге мы попробуем понять и выяснить вместе с читателем. Также я думаю, что в геометрии давно произошла революция и переосмысление самого понятия «геометрия», что само понятие имеет не только одномерное понимание как Евклидова геометрия, но и существуют наряду с первой и геометрия Лобачевского, геометрия Римана, топология и другие, поэтому, возможно, настало или назрело время совершать революцию и в таком фундаментальном понятии, как «тригонометрия», расширив его до понятия «дерадианная тригонометрия». С расширением понятия «геометрия» произошла параллельно революция в физике, астрономии и других разделах естествознания, в которых появились в первую очередь такие теории, как квантовая физика, термодинамика, теория относительности и так далее, без которых современная наука просто немыслима и в которых «новые геометрии» играют основополагающую роль, поэтому еще неизвестно, к каким новым открытиям и свершениям может привести расширение понятия «тригонометрия», или, возможно, это лишь мои только желания, ничем не подкрепленные, но, как бы то ни было, этим все равно надо заниматься, и на то и существуют математики, в том числе и математики-любители, которые как первопроходцы и энтузиасты идут впереди, освещая и размечая путь, по которому уже могут пройти и проложить основательные рельсы настоящие профессионалы своего дела — ученые разных областей знания.

Хахалкин Ю. Н

03.02.2025

Глава 1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ДЕРАДИАННЫХ ДРОБЕЙ

Дерадианный треугольник. Дерадианный угол. Дерадианная дробь

В геометрии Евклида есть базовое и фундаментальное понятие угла, и оно звучит так:

угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки (которая называется вершиной угла).

Это понятие угла нам интуитивно понятно, и мы уже давно привыкли к нему, с самого раннего детства, но я бы хотел дать немного другое определение, которое рассматривает угол немного с иного ракурса, чем наше обычное представление этого замечательного понятия, это новое определение и понимание угла дало бы нам более полное раскрытие и дополнение к уже существующему общепризнанному знанию. А также ввести еще два важных понятия: дерадианный треугольник и дерадианная дробь.

Определение 1

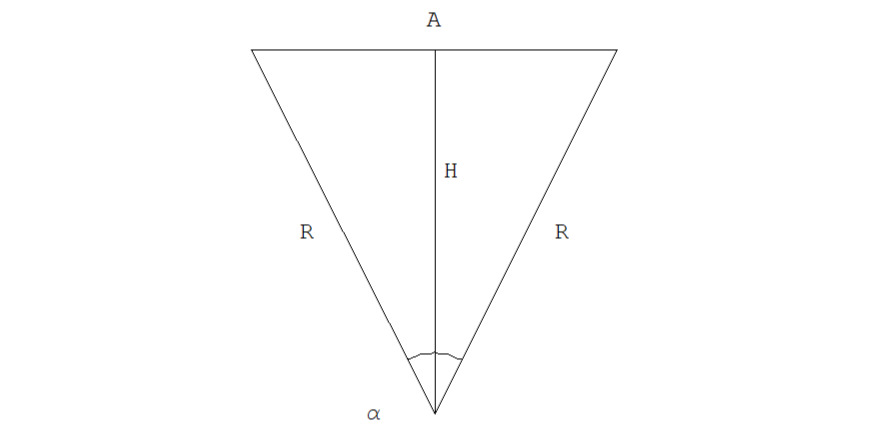
Дерадианный треугольник — это равнобедренный треугольник с углом альфа при вершине, в котором угол задается какой-либо парой чисел:

{M, N}, где A — это длина основания (называемая апофемой угла) этого равнобедренного треугольника, H — высота угла этого равнобедренного треугольника, а R — гипотенуза угла этого равнобедренного треугольника, и такой треугольник всегда будем называть дерадианным треугольником ABC и обозначаться на письме d (ABC).

См. рис. 1.1.1.

Определение 2

Дерадианный угол — это, угол который задается какой-либо парой значений {M, N}, где пара чисел — это всегда какие-то два элемента из множества {A, H, R}, которые принадлежат дерадианному треугольнику d (ABC), и такой угол обозначается:

…… … … … … … (A & H) = [A & R] = {H & R}

Есть еще обратные, называемые мной транспонированные дерадианные углы (или дроби) — это обычная дробь, только перевернутая, тот аргумент, который был в числителе, становится в знаменатель, и наоборот, тот аргумент, который был в знаменателе, становится в числитель, и обозначаю:

…… … … … … ((A & H)), [[A & R]], {{H & R}}

Но пока мы такие дерадианные дроби рассматривать не будем.

Определение 3:

Дерадианная дробь — это запись-обозначение дерадианного угла дробью вида:

…… … … … α ≡ (A & H) = [A & R] = {H & R}

…… … … … (A & H) ≠ (0 & 0), [A & R] ≠ [0 & 0]

…… … … … … … … … … … …. {H & R} ≠ {0 & 0}

И записывается в квадратных, круглых или иных скобках, а также где M — это числитель дерадианной дроби, а N — знаменатель дерадианной дроби.

В настоящей записи дерадианные дроби записываются так: см рис.1.1.2.

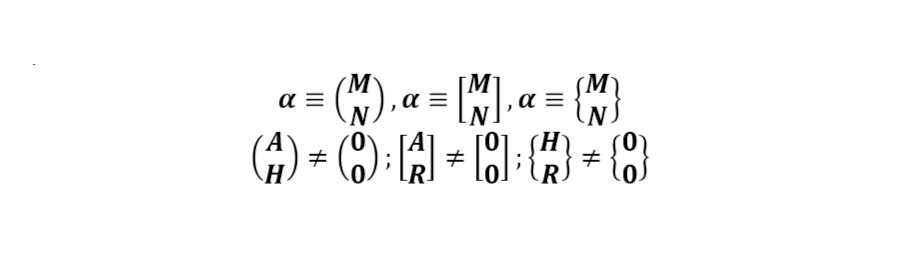
Но, так как я не могу их так изображать, мой редактор книги этого не позволяет делать, то я буду писать в строчку, но надо всегда помнить, что чисто математическое, алгебраическая их запись — это запись в столбец.

Определение 4

Дерадианная дробь первого типа (или тангенциальная де-дробь) для угла при вершине альфа в дерадианном треугольнике — это (всегда выражение, записываемое в круглых скобочках) соответствие апофемы к высоте:

…… … … … … α ≡ (A & H), -2R≤A≤2R

…… … … … … … … …..A∈ℝ, H∈ℝ, R∈ℝ

И читается: угол альфа соответствует дерадианной дроби первого типа — апофема А к высоте Н, или сокращенно — А к Н.

Определение 5

Дерадианная дробь второго типа (или синусоидальная де-дробь) для угла при вершине альфа в дерадианном треугольнике — это (всегда выражение, записываемое в квадратных скобочках)

соответствие апофемы к биссектрисе:

…… … … … … α ≡ [A & H], -2R≤A≤2R

…… … … … … … … ….. A∈ℝ, H∈ℝ, R∈ℝ

И читается: угол альфа соответствует дерадианной дроби второго типа: апофема А к гипотенузе R, или сокращенно — А к R.

Определение 6

Дерадианная дробь третьего типа (или косинусоидальная де-дробь) для угла при вершине альфа в дерадианном треугольнике — это (всегда в фигурных скобочках) соответствие высоты к биссектрисе:

…… … … … … α ≡ {H & R}, -R≤H≤R

…… … … … … … … ….. A∈ℝ, H∈ℝ, R∈ℝ

И читается как: угол альфа соответствует дерадианной дроби третьего типа высоты Н к гипотенузе R, или сокращенно — H к R.

Напоминание 1

В числителе дерадианной дроби n-го типа всегда стоит какой-то из катетов половинного дерадианного треугольника: или A, или H.

Напоминание 2

Параметры дерадианного треугольника для лучшего запоминания лучше в уме упорядочить по старшинству:

{A, H, R}, сначала идут катеты, потом гипотенуза для прямоугольника половинного угла.

Дроби типа (0 & 0), [0 & 0], {0 & 0} считаются неопределенными (но не невозможными) или определены только как дроби центра окружности, обладают таким свойством: что с ними ни делай, как ни преобразуй, они всегда будут равны сами себе, — это главное свойство этих дробей, я их называю «неизменяемые дроби», или «дроби точки отсчета».

Дерадианные дроби — это аналоги своего рода функций Tan (x), Sin (x), Cos (x), только уже не для прямоугольного треугольника, а для равнобедренного, или, еще можно иначе сказать, дерадианного треугольника, и не деление катета на гипотенузу, а их приведение или их бинарный набор. Также в обычной тригонометрии, я бы назвал ее тригонометрией прямоугольного треугольника, для нахождения параметров треугольника и углов существуют основные понятия синуса, косинуса, тангенса и других тригонометрических функций, а в тригонометрии же дерадианного треугольника, если мы знаем дерадианные дроби углов, эти функции решаются намного проще, все углы можно находить без каких-либо сложных вычислений, поэтому в нашем случае теорию дерадианных дробей можно смело назвать тригонометрией равнобедренного треугольника, поэтому я и дал такому равнобедренному треугольнику особое название — дерадианный треугольник, дабы отделить его от всех прочих треугольников.

Дерадианную дробь первого типа я не зря поставил первой, она сходственна тангенсу прямоугольного треугольника, но для меня она дороже всех других типов дробей, с нее все и началось, благодаря ей я увидел и осознал всю красоту и силу данной теории, благодаря ей я понял, что это не просто наборы каких-то значений, а новая дисциплина в математике и, в частности, в тригонометрии, и мне с ней проще всего работать: у нее самые короткие, простые и понятные решения в задачах, также дерадианные дроби других типов проще всего решать и выражать через дерадианную дробь первого типа, поэтому и поставил ее на первое место, а не на третье, как это делается в тригонометрии для функции тангенса, возможно, в последующем все изменится и обозначаться и называться все это будет по-другому, я не против и буду только рад. Для меня главное сейчас — это обозначить суть явления и поставить круг задач для этой новой теории, теории дерадианных дробей, а остальное со временем благодаря уже тому, кто будет продолжать и систематизировать эту дисциплину, встанет на круги своя, и тогда уже эта дисциплина будет или, возможно, новым разделом тригонометрии и станет таким же привычным, как другие разделы математики, вырастет в настоящее полноценное математическое знание, или откинется как не имеющая особого смысла, а пока пусть будет как-то так.

Хорошо, давайте подытожим: дерадианный угол, дерадианный треугольник, а также дерадианная дробь — это три центральных понятия теории дерадианных дробей. Вокруг них в основном и происходят все основные действия.

Далее условимся всегда понимать и обозначать:

а) на чертеже дерадианный треугольник d (ABC) чертить вершиной вниз, а основанием или апофемой — вверх, как на рисунке 1.1.1;

б) угол при вершине на рисунке по умолчанию, если другое не оговорено, всегда будет (1& 1), т.е. (A =1, H=1). Так будет удобно в дальнейшем понимать, что перед нами конкретно дерадианный треугольник, а не какой-то другой, также это будет удобно в дальнейшем при изучении свойств, рассмотрении чертежа при доказательстве теорем и т. д.;

в) обозначение (M& N) (в круглых или других скобках) будем называть дерадианной дробью n-го типа, дерадианный угол и дерадианная дробь — это синонимы. Обозначают один и тот же геометрический объект или геометрическую фигуру, а именно: угол, который находится при вершине дерадианного треугольника.

Дерадианный угол — это геометрический объект, а дерадианная дробь — алгебраический. Одно понятие сугубо геометрическое, другое алгебраическое;

г) пару M и N, апофему и высоту или иные парные параметры дерадианного треугольника обозначать на письме как:

…… … … … … … … … …. …. α ≡ (M& N)

и читать как «угол альфа соответствует дерадианной дроби n-го типа M к N».

Наименования числителя и знаменателя менять местами нельзя!!!

…… … (M & N) ≠ (N & M), [M & N] ≠ [N & M],

…… … {M & N} ≠ {N & M}

Так как это сродни и аналогично делению в тригонометрии прямоугольного треугольника противолежащего катета (или прилежащего) на гипотенузу, но не наоборот.

Апофема никогда не бывает в знаменателе, так же как гипотенуза никогда не бывает в числителе дробей (кроме транспонированных де-дробей). Сами, конечно, М и N можно численно менять местами, эту операцию назовем реверсированием дерадианной дроби, а вот уже сами названия и наименования менять местами нельзя, иначе это уже будет иной тип дроби, а не исходный;

д1) Существует два типа записи дерадианных дробей: в столбик и в строчку, — в этой книге мы в основном пишем все де-дроби в строчку, но вообще намного нагляднее писать в столбик (см. рис. 1.1.3).

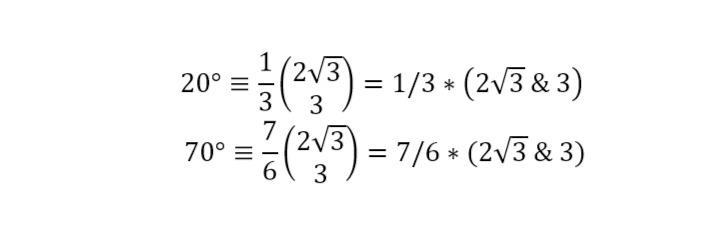
Рис 1.1.3. Пример записи одного и того же выражения двумя способами. Другие дроби других типов так же можно записать, но только в квадратных или фигурных скобках.

д2) числитель M дерадианной дроби писать всегда сверху (в начале при перечислении), а знаменатель N — снизу (после):

…… … … … …… (M & N), [M & N], {M & N}

е) запись дерадианной дроби типа, где знаменатель N дерадианного треугольника равен единице,

…… … … … … … … … …. …. (M & 1) = (M)

будем называть приведенной дерадианной дробью n-го типа.

е1) дерадианный треугольник d (ABC) всегда имеет вершину в точке С, а A, B — внутренние углы B, C при апофеме, и боковую сторону также называть просто гипотенузой дерадианного треугольника и обозначать R;

ж) верхнее и нижнее значение дерадианной дроби называть, как и в обычных дробях, числителем и знаменателем дерадианной дроби;

з) боковую сторону дерадианного треугольника обозначать прописной заглавной латинской буквой R и называть гипотенузой дерадианного треугольника для наибольшей простоты;

и) также будем всегда стараться вверху обозначать градусную меру угла, αr — в радианах, αd — в дерадианах, α° — в градусах и т. д.

к) если апофема, высота или гипотенуза принадлежат углу альфа (у каждого угла любого треугольника есть свое множество {A, H, R}), то обозначать на письме с индексом того угла, к которому апофема, высота или гипотенуза принадлежат:

…… … … … … … … … …. Aα∈α, Hα∈α, Rα∈α

л) дробь для угла фактического треугольника с заданными не приведенными параметрами называть истинной дерадианной дробью, или фактической дерадианной дробью, и все, что с ней связано, также называть истинным: истинная апофема, истинная высота, истинная гипотенуза и т. д., а на письме обозначать:

…… … … … … … … … …. …. … … ….. {Af, Hf, Rf}

м) иногда слово «дерадианная», «дерадианный» будем опускать или просто сокращать на письме и писать: де-дробь, дерад., дробь, д.д. угол, д/д треугольник и т. д. или же вовсе без добавления прилагательного, но только тогда, когда понятно из контекста, о чем идет речь, о каком элементе мы пишем;

н) дробь вида (0 & 0) считать неопределенной. Геометрически такой дроби соответствует точка начала координат или точка центра окружности;

о) также хочу уточнить: апофема — это не апофема высоты боковой грани тетраэдра, нет, это слово означает в этой теории свой самостоятельный смысл, а именно: основание дерадианного треугольника. Конечно, в дальнейшем могут быть проблемы, когда дерадианный угол будет распространен на трехмерное пространство и как раз в тетраэдре, но пока трехмерный случай дерадианного угла мы не рассматриваем. Это название «апофема» пока условное, в случае чего его всегда можно поменять на какое-то другое, я не возражаю;

п) углы рассматривать на первом этапе только на промежутке от нуля до пи радиан [0, π], не вводя пока что отрицательных углов. Это пределы обычного плоского угла в произвольном самом обычном треугольнике;

р) высоту, проведенную от конечной точки одной гипотенузы к основанию другой гипотенузы, будем называть высотой гипотенузы, и обозначать hR;

с) окружность радиуса, равного длине гипотенузы дерадианного треугольника над апофемой, будем называть в дальнейшем радиантом (сейчас многое непонятно, что здесь написано, но в дальнейшем все разъяснится и станет очевидным);

т) такие скобочки в записи дроби 【…】говорят о том, что правило, теорема, свойство и т. д. подходит одновременно сразу ко всем типам дерадианных дробей, например:【M& N】 — дерадианная дробь, да, это так, так как любая из дробей (M& N), [M& N], {M& N} является по определению дерадианной.

Что отличает в первую очередь дерадианный угол от обычного угла? Это то, что дерадианный угол всегда задается двумя известными значениями из трех возможных и также не может обходиться без числителя и знаменателя (апофемы и высоты для тангенциальной дроби), даже в случае если числитель или знаменатель равен 0, то он все равно существует, просто значение его равно нулю. И это касается всех составных частей дерадианного треугольника. В отличие от обычного угла, где в обычном понятии угла в евклидовой геометрии есть только вершина и два луча, исходящие из общей точки, то в случае с дерадианным углом угол — это два луча (отрезка), которые пересекает апофема, и перпендикулярно апофеме высота. Поэтому мы дерадианный угол не можем рассматривать как полноценный угол, но считаем его новым математическим объектом в геометрии, что-то среднее между понятием угла и понятием треугольника.

То есть, дерадианный угол объединяет в себе сразу одновременно два понятия: и угол, и треугольник.

В этом понятии сразу объедены два представления: и алгебраическое, и геометрическое. Также дерадианный угол является для теории дерадианных дробей таким же центральным объектом, как и прямоугольный треугольник в обычной, классической тригонометрии, пишу «обычной», потому что думаю и, возможно, наивно верю, что есть еще тригонометрии, помимо обычной, построенной на прямоугольном треугольнике и числе Пи. Понимаю, звучит непривычно и чересчур новаторски, но об этом и пойдет речь дальше в этой книге для большего понимания самой идеи. А сначала сосредоточимся на основных понятиях — без них никак не приоткрыть завесу множественности тригонометрий. Ну хорошо, продолжим далее изучение новой концепции угла. Иногда угол альфа определяют тангенсом угла, то есть отношением двух значений: a и b, а/b, — то есть их прямым отношением-делением, отношением-делением двух катетов прямоугольного треугольника:

…… … ...Sin (α) =a/c, Cos (α) =b/c, Tan (α) =a/b

И вообще, как мы знаем, все прямые тригонометрические функции определяются отношением катета к гипотенузе, катета к катету и т. д., но, в отличие от тангенса или других тригонометрических функций, дерадианный угол определяется на самом деле самым настоящим набором двух значений: числителем и знаменателем {M, N}. Конечно, возможна и вторая интерпретация, тоже отношением, но это только для численных углов (угловая тангенциальная измерительная система УТИС), а не как с тангенсом угла или другими тригонометрическими функциями, только отношением и ничем другим. То есть всегда есть выбор: либо угол обозначать набором двух чисел, либо отношением этих двух чисел, т. е. десятичным числом. Также главное в дерадианных дробях как нового объекта математики — это не то, что мы угол можем задать простым отношением, например, гипотенузы к высоте, и выразить как-то по-«тригонометрически», а именно вся суть новизны и есть, и скрывается в том, что это именно набор двух значений. Если бы это было просто отношением двух каких-то величин, то тогда мы бы просто «скатились» к «обычной» тригонометрии и тригонометрическим выражениям, и на этом бы все и закончилось, но в случае с дерадианными дробями появляется новый самостоятельный объект, который нужно изучать и развивать, обогащая новыми знаниями, описывая его на основе аксиом данной теории, которые в той или иной степени описывали бы эту дробь и ее математические характеристики, и саму суть его природы. В этом и есть суть моей теории, именно в понимании этого объекта и внесении его в общую математику целиком, как в свое время внедряли комплексные числа на рубеже XV века. Я раньше, в прошлом, долго решал углы только через тригонометрические функции, хотя я тогда уже знал и оперировал понятием апофемы и высоты, и все равно как-то долго не доходило, что это не просто отношение, а что-то более этого, и, чтобы понять, что углы — это не просто сложение или умножение половинных тангенсов, а наборы двух значений апофемы и высоты, и вот на осознание этого факта мне понадобилось много времени, также я раньше углы в равнобедренном треугольнике точно так же воспринимал, как в современной тригонометрии, просто через отношение двух величин, точно так же, как, например, считаем, что:

…… ….Sin (α) =a/c, Cos (α) =b/c, Tan (α) = a/b

Но, чтобы понять, что это отношение не просто отношение, а дробь вида:

…… … α ≡ (A & H) = (2Tan (α/2) & 1) = (2Tan (α/2))

вот в этом трудность основная и была, так как эта дробь совсем не очевидна, хоть и находится на виду. При решении задач по геометрии меня все время относило в «обычную» тригонометрию. А на самом деле новая тригонометрия строится на предшествующей тригонометрии, как я ее еще называю, тригонометрии прямоугольного треугольника, и без обычной тригонометрии невозможно построить нового здания уже следующей дерадианной тригонометрии, потому что дерадианная геометрия — это уже продолжение «обычной» тригонометрии и произрастает на ее фундаменте и основании, обычная тригонометрия как бы питает, вскармливает и дает базу и почву для дерадианной тригонометрии, также новая тригонометрия произрастает и на почве или базе теории комплексных чисел и многих других базовых теориях. Ну ладно, далее вы и сами все это поймете. И, возможно, поняв саму концепцию, уже сможете сами решать какие-то задачи точно так же, как и я, не все (где-то достаточно и обычной геометрии и тригонометрии), но какие-то — точно. В этой книге даются не просто новые понятия, но способы решений задач не как обычно, стандартными способами, но, применяя дерадианные дроби, находить ответы немного по-другому, чуть-чуть нестандартно. И скажу, что при решении обычных геометрических задач хватает и стандартных методов современной геометрии и тригонометрии, у теории дерадианных дробей существуют свои собственные задачи, в основном это задачи по поиску неизвестных параметров апофемы высоты и гипотенузы углов и всего, что с ними связано, даже если это иногда кажется и не совсем понятным занятием, но это суть этой теории и ее главный смысл, также у этой теории при решении задач существуют свои дополнительные построения геометрических объектов, доказательства теорем и много чего другого интересного, что есть и в обычной геометрии и тригонометрии. В общем, как мне кажется, эта теория вполне самодостаточна и продуктивна.

Помню, когда я наконец-то осознал существование таких дробей, меня это тронуло до глубины души, и это было просто как какое-то озарение, как будто какая-то вспышка в моем сознании произошла, и я сразу понял, что мне надо от математики и в каком направлении двигаться дальше. Почему такое странное название — deradian? Потому что с латинского de — два, двойной, radian — радиан, единица измерения угла, то есть можно перевести как «двойной угол, двойное измерение угла» и т. д. Но еще раз хочу подчеркнуть, что формально это не только угол в обычном понимании евклидовой геометрии, и не только плоский треугольник, но что-то среднее между ними: и угол, и треугольник одновременно. Численно при алгебраическом написании это обычный угол, который как-то задается через какие-то две части дерадианного треугольника, а геометрически это выглядит как равнобедренный треугольник.

Так как это понятие ново в математике (мне кажется, но не достоверно, похоже, что в древности чем-то подобным вроде как астрономы и мореплаватели, возможно, пользовались, похожей мерой для угла в астролябии в виде разных измерительных инструментов типа градштока, трикветра и разного рода конструкций астрономических посохов, см. рис.1.1.4), поэтому мне и пришлось самому придумывать этому понятию имя, просто в то время еще не могли понимать и осознавать теорию дерадианных дробей как полноценную теорию, так как тригонометрия тогда еще только-только зарождалась и даже понятия синуса, косинуса, тангенса угла не совсем точно понималось математиками той эпохи, хоть уже и вовсю пользовались отношениями сторон в измерениях углов наклона до светил и, конечно, осознать всей полноты тогда еще не совсем могли. Так как я не нашел ничего аналогичного в современной математике, поэтому пускай пока будет такое название, возможно, в будущем оно и приживется и все будут им оперировать так же, как сейчас оперируют понятиями «точка», «дуга», «луч», «прямая», «угол», «хорда», «гипотенуза» и т. д.

Оказывается, в технической литературе есть аналогичное понятие — это понятие «конусность».

Определение

Конусность (К) — это отношение диаметра окружности конуса (D) к его высоте (H):

…… … … … … … … … …. …. … … … K=D/H

Это для полного конуса, а для усеченного конуса конусность (K) равна разности диаметров к расстоянию между ними:

…… … … … … … … … …. …. … … K= (D-d) /L

Также конусность может задаваться углом вершины конуса (α). Половина угла вершины конуса называется уклоном конуса (α/2).

…… … … … … … … … …. …. … … K=2Tan [α/2]

Например, см. рис. 1.1.5.

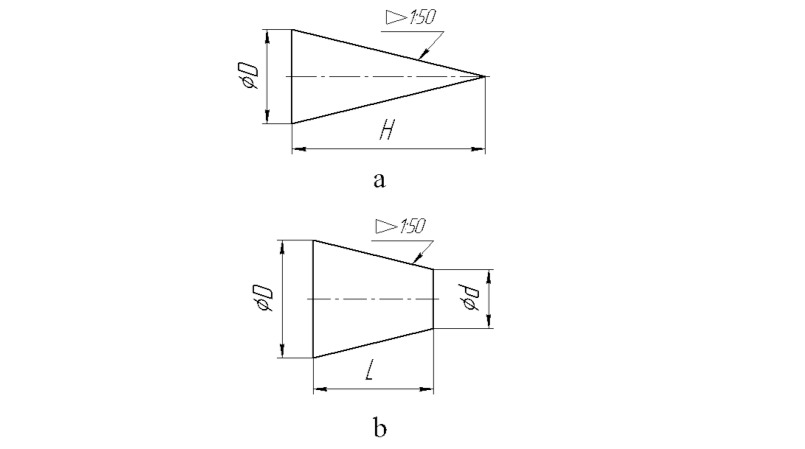
а — полный конус, b — усеченный конус, и в качестве примера приведено условное обозначение конусности по ГОСТ 2.307—68. Также конусность может измеряться в процентах и промилле, и на практике приводятся таблицы конусности, по которым можно определить эту конусность, см. рис. 1.1.6.

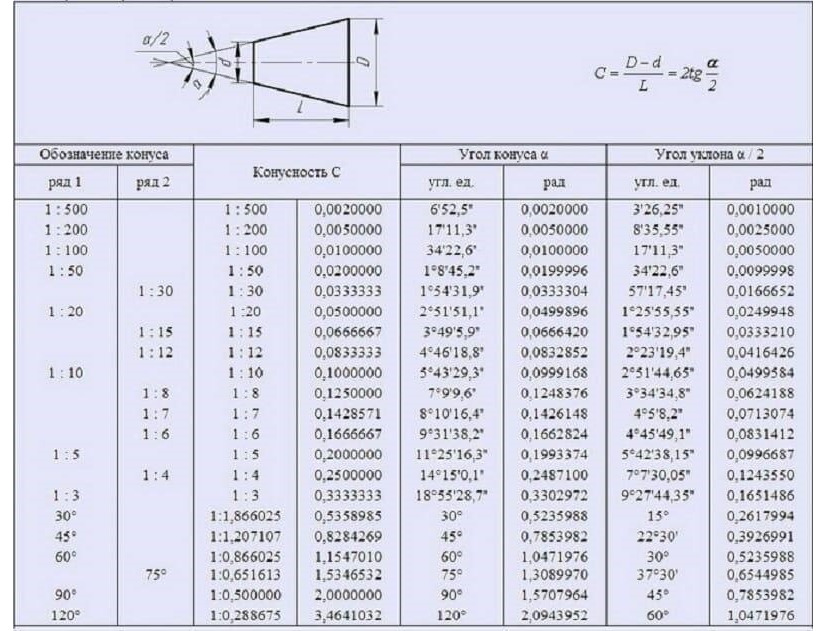
И на этом все, вся теория конусности заканчивается, хотелось бы больше информации иметь, кто и как составляет эти таблицы и есть ли у этого всего какое-то продолжение, как это все устроено на самом деле, ну уже хорошо, что все-таки же есть что-то похожее на нашу теорию в природе, и этой величиной даже прекрасно пользуются, и это хорошо и правильно, но все-таки я бы хотел вернуться к своей теории, которая основана совершенно из других побуждений и построена на других идеях, более фундаментальных, и тем более при написании своей теории я ничего не знал об этом прекрасном понятии. Всегда поражаюсь, что есть прекрасные формулы, как, например, это понятие «конусность», о которых где-то кто-то что-то пишет в каких-то, возможно, НИИ, но в общедоступном месте или общем доступе, несмотря на интернет, никакой информации нет. Поэтому приходится что-то всегда свое придумывать, и никогда заранее не знаешь, возможно, уже все до меня придумано, и я бы просто прочитал литературу и не писал бы и не придумывал бы данную теорию, но, увы, ничего такого нет. Единственное, что еще хочу добавить, что эта теория не имеет никакого отношения к понятию конусности, так как она создавалась не для этого и не под это, конусность — это вторичное понятие или производное понятие от понятия дерадианных дробей, то же самое что понятия скорость, ускорение — производные от понимания дифференцируемости функции — это лишь все определения приложений в других областях знаний, в черчении, например, и это правильно, и так должно быть, прочитав эту книгу, вы в этом и сами убедитесь. Даже потому что эти понятия «конусность» и «дерадианная дробь» создавались независимо друг от друга и в разное время, первому понятию, наверное, уже около ста лет со времен (хотя я его встречаю не ранее чем 1974, возможно, и чуть ранее появилось это понятие), когда начали пушки выливать и разного рода конусные втулки вытачивать и изготавливать на заводах и фабриках, а второе, я сам придумал, будучи молодым студентом в училище, когда мне еще было 17 лет, и, как понимаете, о первом понятии я вовсе тогда даже ничего не знал. Как видим, первое понятие чисто техническое, а второе понятие строго математическое, или алгебраически-геометрическое, и узнал я о понятии конусности совершенно случайно, когда изучал конусы, потому что это фигура вращения относительно высоты дерадианного треугольника, и сильно был удивлен и озадачен, сказать, что я был в изумлении, это значит ничего не сказать, оказывается, вот где находится в природе и как называется похожее понятие, ну и на этом все, я дальше продолжил писать свою книгу, так как понимаю, что я все равно должен это сделать и кроме меня это никто не сделает, и к тому же уже было написано более 70% книги, не бросать же все на полпути. Моя теория ближе к чистой математике, и просто измерять конусность для разного рода конусов мало для математики, и математика оперирует более общими и отвлеченными понятиями от природы объектов.

Так вот, вернемся дальше к нашей теории. Так как дерадианный угол строго связан с треугольником, а как мы знаем, что в треугольнике ни один угол не может превосходить 180°, то и дерадианный угол также не может превосходить 180° или π радиан, то есть если угол в любом плоском треугольнике всегда лежит в пределах:

…… … … … … … … … …. …. … … … 0r ≤ α ≤ πr,

то из этого следует, что и положительная дерадианная дробь будет лежать в пределах

…… … … … … (0& 1) ≤ (A& H) ≤ (1& 0)

…… … … … … [0& 1] ≤ [A& R] ≤ [2& 1]

…… … … … … {0& 1} ≤ {H& R} ≤ {1& 1}

Пока мы не будем рассматривать отрицательные, комплексные, периодические дерадианные дроби или дроби для произвольного угла, ограничимся только пока положительными углами от нуля до Пи радиан [0, π], принадлежащим углам самого обычного произвольного плоского треугольника.

Глава 2. Основные формулы и теоремы теории дерадианных дробей

2.1. Общий вид дерадианной дроби. Главные формулы перехода. Реверсирование и транспонирование дерадианной дроби

В дерадианном треугольнике угол может определяться многими способами, а именно: в зависимости через отношение каких частей мы задаем его дерадианную дробь. А дерадианную дробь мы можем задать через одно из бинарных множеств частей дерадианного треугольника {A, H, R}, попарно разбивая их по два:

…… … …α ≡ (A & H), α ≡ [A & R], α ≡ {H & R}

См. рис. 2.1.1.

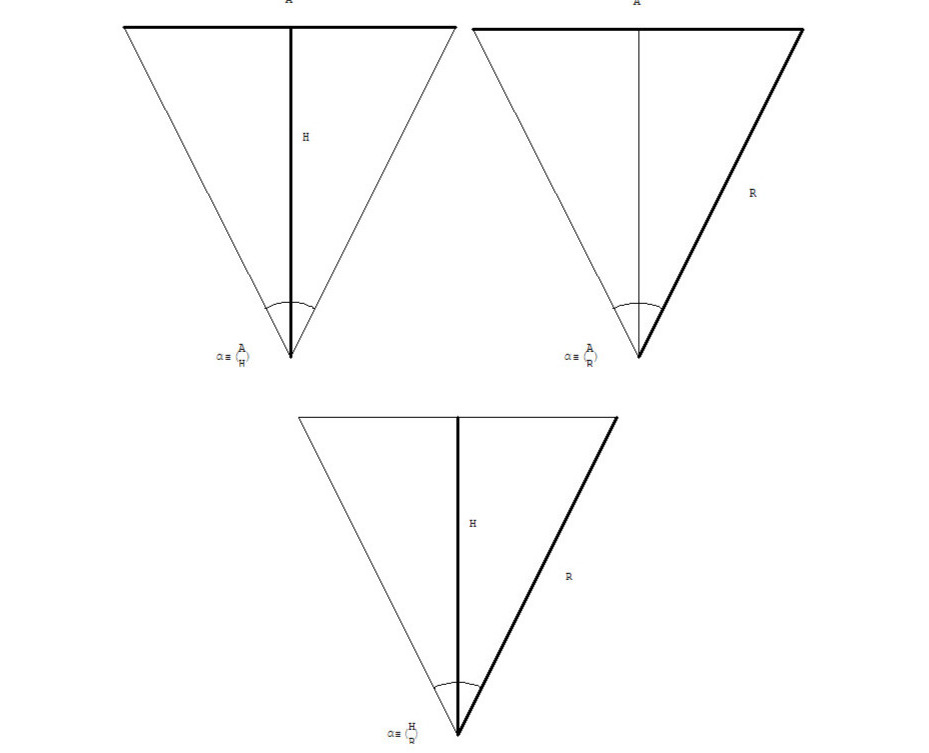
Это и есть три основных типа дерадианных дробей для нашего дерадианного треугольника, возможны и другие дерадианные дроби, обратные этим трем, которые в обычной тригонометрии соответствуют обратным тригонометрическим функциям, секансу и косекансу угла, и другие, но мы их пока рассматривать не будем. Каждая из этих дерадианных дробей имеет свою внутреннюю арифметику и свои математические законы, весьма похожие между собой и в целом дополняющие друг друга, так как связаны между собой обычной классической тригонометрией.

Основное правило для запоминания их точно такое же, как и в классической тригонометрии для трех основных функций.

И звучат они так:

1) Дерадианная дробь первого типа равна приведению противолежащей апофемы к прилежащей высоте. Это утверждение соответствует и очень похоже на определение тангенса угла прямоугольного треугольника.

2) Дерадианная дробь второго типа равна приведению противолежащей апофемы к гипотенузе. Соответствует определению синуса угла прямоугольного треугольника.

3) Дерадианная дробь третьего типа равна приведению прилежащей высоты к гипотенузе. Соответствует определению косинуса угла прямоугольного треугольника.

Почему такая запись? Конечно, мы бы могли записать сразу тернарное множество и не разбивать, возможно, по два элемента, это бы даже нам, возможно, отменило такую странную запись для обозначения угла, но на самом деле и такая запись тоже есть, такое множество я называю тернарным множеством, это множество, в которое входят сразу все три параметра дерадианного треугольника, а именно: где уже присутствуют все три значащие части:

…… … … … … … … … α ≡ (A& H& R)

Такое тернарное множество хорошо описывает общие параметры какого-то угла или какого-то треугольника, как общая характеристика, сразу видно, конкретно какими параметрами обладает угол и к какому дерадианному треугольнику угол принадлежит. Но эту запись мы будем уже использовать для угла известного, или, как условились ранее называть такой угол фактическим, или истинным дерадианным углом, в котором уже известны все три параметра величин треугольника, но когда хоть один из этих параметров неизвестен, тогда и будем прибегать к дерадианной записи угла.

Определение 2.1.1

Истинным, или фактическим, дерадианным углом будем называть угол-αf, для которого известны все три главных его параметра {A, H, R}, не обязательно приведенные, и так же писать такой дерадианный угол на письме через тернарную дробь:

…… … … … … … … … αf ≡ (A& H& R)

Тернарный вид дроби — это запись общего вида угла, так как угол можно записать многими эквивалентными способами, а тернарный вид существует только один для конкретного угла со всеми известными элементами, в этом и состоит основная разница бинарной записи и тернарной, например, для египетского треугольника {3,4,5} три его угла будут выражаться такими тернарными дробями, приведенными, так как в их дроби все параметры сокращены и приведены (см. рис. 2.1.2).

Это две эквивалентные записи, просто в первом случае все параметры приведены и сокращены (о сокращении речь в следующей главе пойдет), а во втором случае нет, и запись напрямую зависит от конкретных сторон треугольника.

Хорошо, в предыдущей главе мы определили, что такое дерадианный треугольник и дерадианный угол, теперь давайте определим точнее, чему могут равняться числитель и знаменатель этих трех типов дробей при разных значениях M и N. Пусть знаменатель всегда для них будет равен одному N=1, так как наш треугольник можно пропорционально масштабировать и угол при этом не изменится, то замасштабируем его так, чтобы N=1, тогда несложно будет найти числитель нашего треугольника, зная угол и знаменатель дроби. Рассмотрим для дроби первого типа:

…… … … … … … … … …. α ≡ (A& H), 0≤α≤π

Применяя теорему синусов и то, что высота всегда перпендикулярна апофеме, а также зная, что в прямоугольном треугольнике всегда действует такое тождество:

…… … … … … … …. … … Sin (α) = Cos (α)

для прилежащих углов, так как они равны, упростив, получим

…… … … …. A/2= Sin (α/2) /Cos (α/2) = Tan (α/2)

Или в итоге найдем, чему равна апофема:

…… … … … … … …. … … A = 2Tan (α/2), 0≤α≤π

И далее, подставив в основную формулу вместо высоты H=1 и вместо апофемы выражение для A, то получим главную формулу перехода для первой дроби от угла альфа к дерадианной форме записи угла первого типа в приведенной форме:

…… … … α ≡ (2Tan (α/2) & 1) = (A & H), 0≤α≤π

Или то же самое, но уже немного в другой форме:

…α ≡ (2 & Cot [α/2]) = (2Sin [α/2] & Cos [α/2]) =

…… … … … … … … … … ……= (A&H), 0≤α≤π

См. рис. 2.1.3.

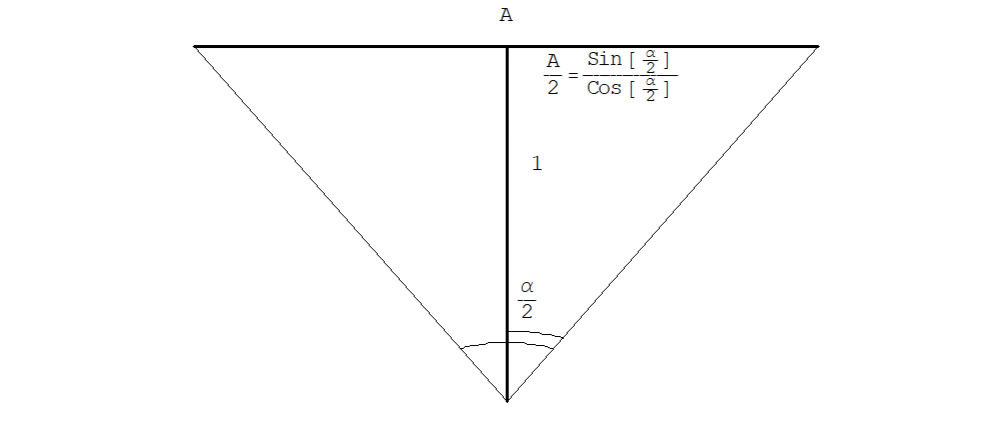
…… … … … … … … α ≡ (2Tan (α/2) & 1), 0≤α≤π

Эта запись в круглых скобочках и есть обозначение обычного геометрического угла через приведенный дерадианный угол первого типа:

…… … … … … … … … …. α ≡ (A & H), 0≤α≤π

Такую запись мы и назовем дерадианной дробью 1-го типа и будем всегда писать ее в круглых скобочках. Также если выразить тангенс половинного угла через синус и косинус, то можно прийти к такому виду дерадианной дроби первого типа, тем самым избавившись от половинного угла:

…… … … … …α ≡ (2Sin [α] & 1+Cos [α]), 0≤α≤π

Подытоживая, скажем, что существует три основных формулы для дерадианной дроби первого типа и все они между собой равны.

…α ≡ (2Tan (α/2) & 1) = (2Sin (α/2) & Cos (α/2)) =

…… … … … …..= (2Sin (α) & 1+Cos (α)), 0≤α≤π

Первая дробь называется приведенной тригонометрической дерадианной дробью первого типа, вторая и третья дробь называются неприведенной тригонометрической дерадианной дробью первого типа. Третья дробь также называется тригонометрической дерадианной дробью единичной окружности.

То есть эта запись всегда актуальна, когда угол α находится через апофему и высоту дерадианного треугольника.

Из главной формулы перехода хорошо видно и доказывается, что, так как любой угол в любом произвольном треугольнике находится в пределах:

…… … … … … … … … …. …. … … …0r ≤ α ≤ πr

то любой угол альфа всегда можно представить и единственным образом, однозначно, до порядка эквивалентных дробей в виде приведенной дерадианной дроби, то есть для любого угла альфа всегда найдется однозначно такая пара {A, H}, что любой угол альфа будет выражаться этой парой:

…… … … α ≡ (A& H), 0≤α≤π, 0 <A <2R, A∈R+

R+ — множество всех положительных вещественных чисел, пока рассматриваем только положительный угол, несмотря на то что у половинного тангенса существуют и отрицательные значения.

Пример 1:

…… … … …α = (π/2) r ≡ (2Tan ((π/2) /2) & 1)) =

…… … … … … … = (2Tan (π/4) & 1)) = (2& 1)

См. рис. 2.1.4.

Пример 2:

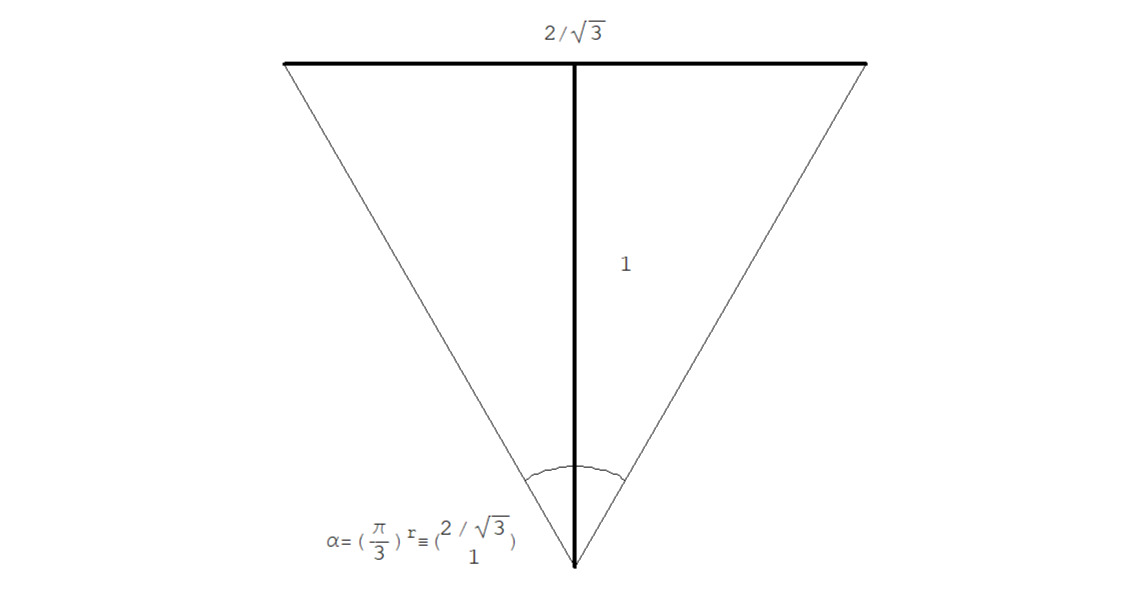
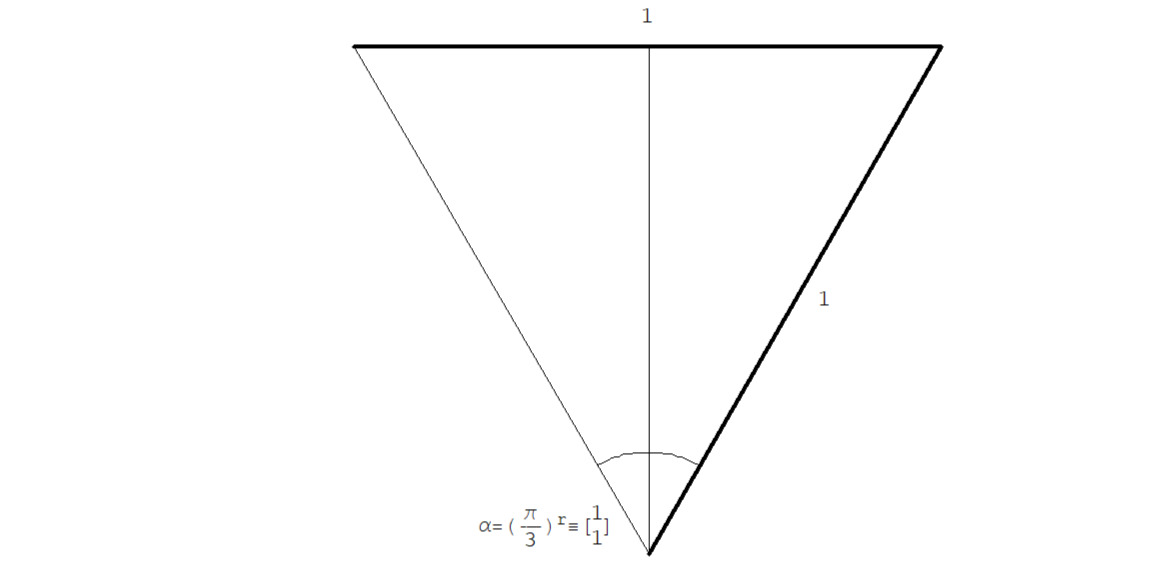
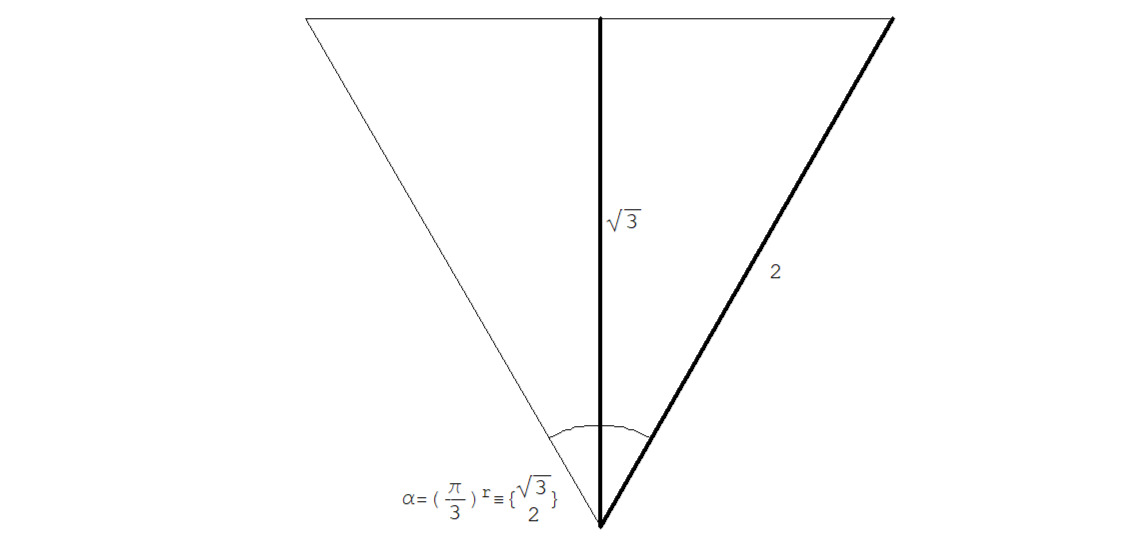
…… … … … α = (π/3) r ≡ (2Tan ((π/3) /2) & 1) =

…… … … … … = (2Tan (π/6) & 1)) = (2/√3 & 1)

См. рис.2.1.5.

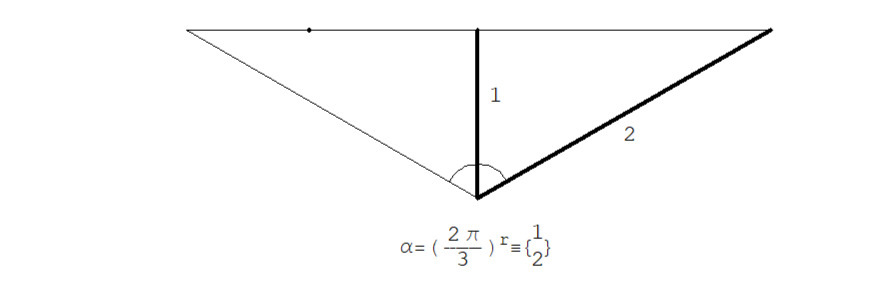
Пример 3:

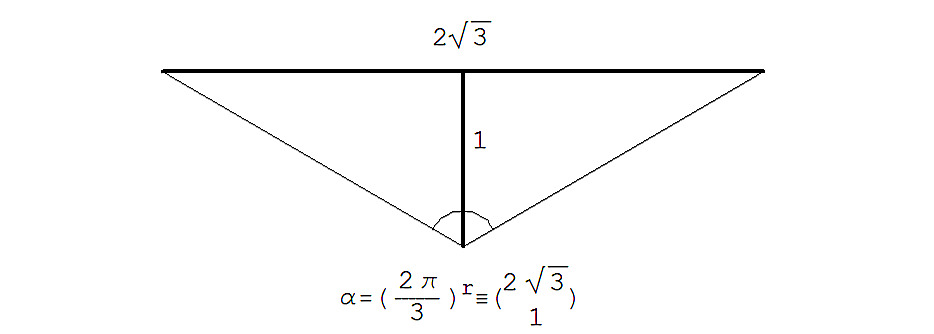
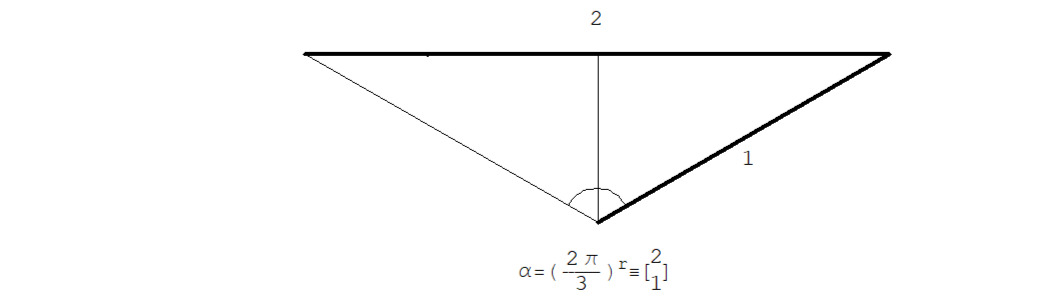
…… … … …α = (2π/3) r ≡ (2Tan (2π/3) /2) & 1)) =

…… … … … … …= (2Tan (π/3) & 1)) = (2√3 & 1))

См. рис. 2.1.6.

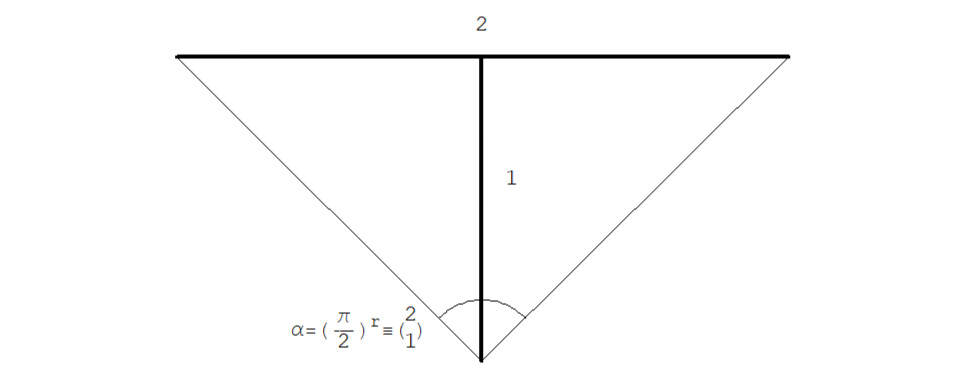
Также актуальна такая формула для большинства распространенных углов:

…… … … … … … … …..α ≡ (2& Cot (α) +Csc (α))

Теперь, когда мы написали и вывели формулу для дерадианной дроби первого типа, давайте рассмотрим главную формулу перехода второго типа для второй дерадианной дроби. Как видно, в ней уже участвуют A-апофема и R-гипотенуза, и записывается она уже в квадратных скобочках:

…… … … … … … … … … …α ≡ [A& R], 0≤α≤π

Находится она точно так же, как и первая де-дробь, только уже через синус половинного угла:

…… … … … ..Sin (α/2) = (A⁄2) /R, A=2Sin (α/2) R

См. рис. 2.1.7.

Так как мы сказали ранее, что знаменатель равен единице, R=1, то числитель дроби или апофема будет равна: A=2Sin [A/2], при R=1, окончательно подставив в дробь получим:

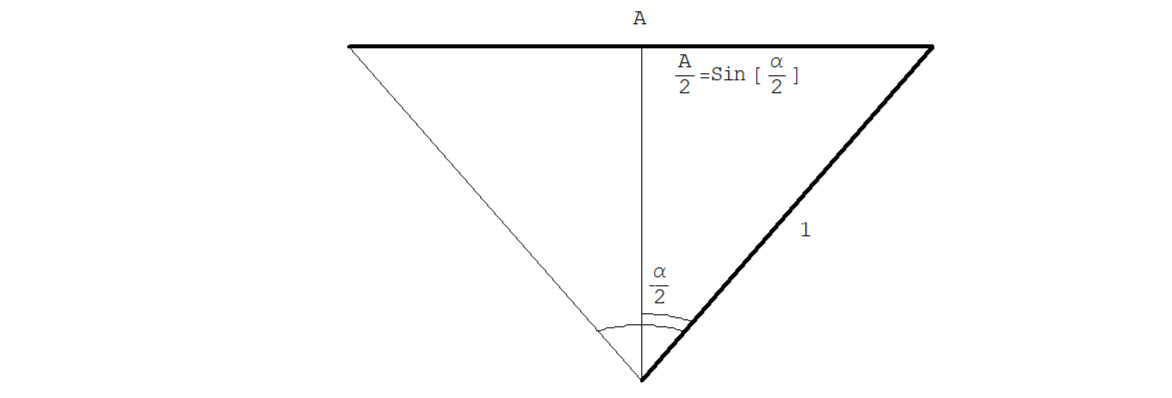
…… … …α ≡ [2Sin [α/2] & 1] = [A& R], 0≤α≤π

Или то же самое, но уже немного в другой форме:

…… … … α ≡ [2& Csc [α/2]] = [A& R], 0≤α≤π

…… … … … … … … α≡ [2√ (1-Sin [α]) & √2] =

…… … … … …..= [√ (2—2Sin [α] & 1)] = [A& R]

Это все записи одного и того же угла в дерадианной форме второго типа. Например, для тех же углов, что были в первых примерах:

Пример 4:

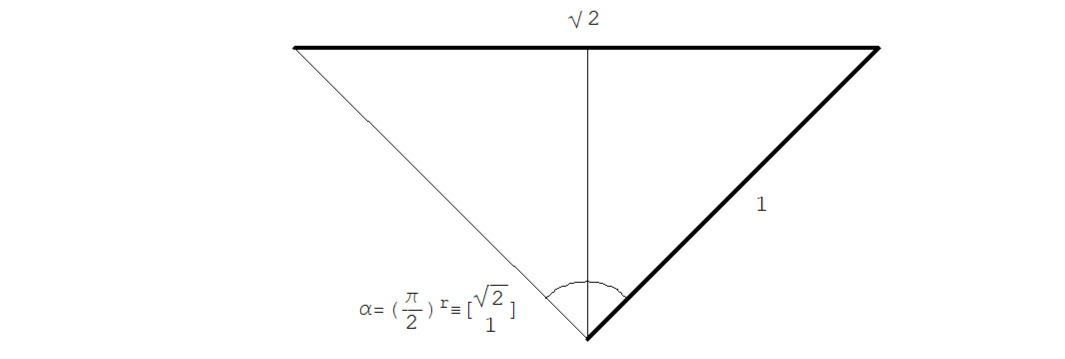
…… … … … α = (π/2) r ≡ [2Sin ((π/2) /2& 1)] =

…… … … … … ……= [2Sin (π/4) & 1] = [√2& 1]

См. рис. 2.1.8.

Пример 5:

…… … … … …α = (π/3) r ≡ [2Sin ((π/3) /2) & 1] =

…… … … … … … … …= [2Sin (π/6) & 1] = [1& 1]

См. рис. 2.1.9.

Пример 6:

…… … … … α = (2π/3) r ≡ [2Sin ((2π/3) /2) & 1] =

…… … … … … … … …= [2Sin (π/2) & 1] = [2& 1]

См. рис. 2.1.10.

Как видим, сама основная идея дерадианных дробей ну очень проста. Но, чтобы к ней прийти, мне пришлось много времени потратить на осмысление нужности и полезности этих дробей. Но математики для этого и существуют, чтобы все время заново переосмысливать какие-то старые и, возможно, уже даже всеми забытые правила и истины, и ставить их на современные рельсы осмысления и понимания новой парадигмы.

Ну хорошо, продолжим дальше размышлять по поводу дерадианных дробей, и последняя основная формула для третьего типа дерадианной дроби в фигурных скобках будет все по тому же принципу, только уже ищем дерадианную дробь через косинус половинного угла:

…… … … … ….Cos [α/2] =H/R;H=Cos [α/2] R

См. рис. 2.1.11.

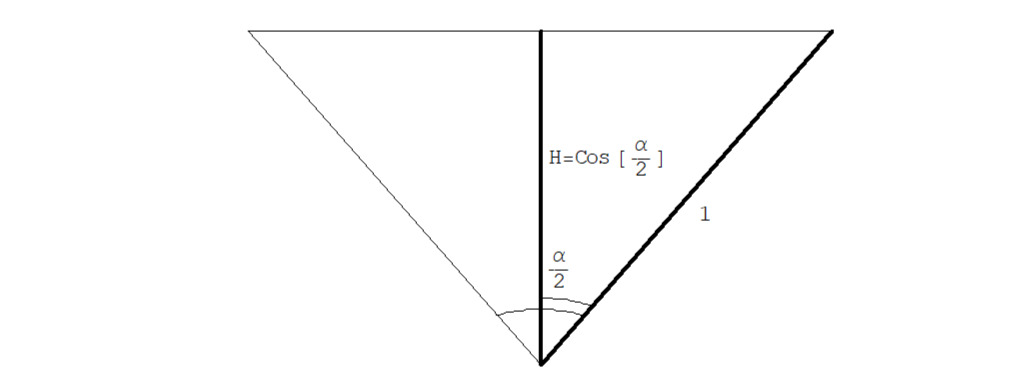
В этом случае единице уже будет равняться R; R=1, а значит, подставив в дробь, где H будет числителем, а R=1 — знаменателем, получим новую дерадианную дробь, обозначим ее через фигурные скобки:

…… … … … … …..α ≡ {H& R} = {Cos (α/2) & 1} =

…… … … … ….. …..= {2Cos (α/2) & 2}, 0≤α <π

Или тоже самое, но уже немного в другой форме:

…… …..α ≡ {1& Cos (α/2)} = {H& R}, 0≤α <π

…… … … … … … … α ≡ {2√ (1+Cos [x]) & √2} =

……..= {√ (2+2 Cos [x]) & 1} = {H& R}, 0≤α <π

И опять рассмотрим примеры, так же как и в первом и втором случаях для тех же углов.

Пример 7:

…… … … ……α = (π/2) r ≡ {2Cos ((π/2) /2) & 2} =

…… … … … … … …= {2Cos (π/4) & 2} = {√2& 2}

См. рис. 2.1.12.

Пример 8:

…… … … …..α = (π/3) r ≡ {2Cos ((π/3) /2) & 2} =

…… … … … … … = {2Cos (π/6) & 2} = {√3& 2}

См. рис. 2.1.13.

Пример 9:

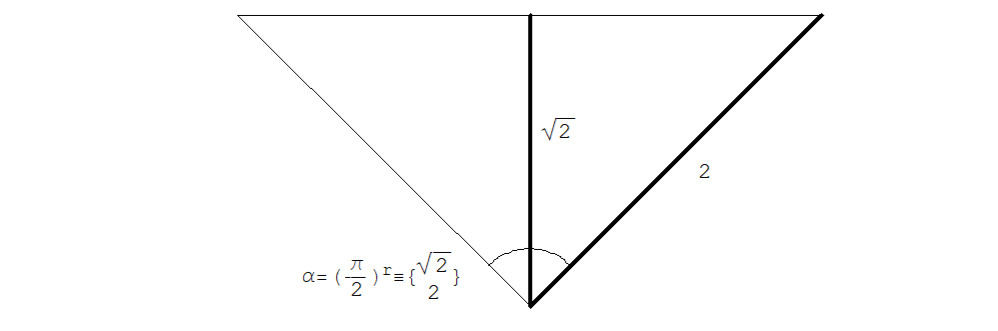
…… … …α = (2π/3) r ≡ {2Cos ((2π/3) /2) & 2} =

…… … … … … … = {2Cos (π/3) & 2} = {1& 2}

См. рис. 2.1.14.

Давайте еще раз выпишем эти замечательные главные формулы перехода к дерадианным дробям трех основных типов и запомним их, тем более что это сделать совсем не сложно, в дальнейшем они нам еще очень пригодятся:

…… … … … …..α ≡ (A& H) = (2Tan (α/2) & 1)

…… … … … …..α ≡ [A& R] = [2Sin (α/2) & 1]

…… … …α ≡ {H& R} = {Cos (α/2) & 1}, 0≤α≤π

Определение 2.1.2

Дерадианные дроби, в которых участвуют тригонометрические функции, будем в дальнейшем называть тригонометрическими дерадианными дробями, которые в свою очередь делятся на приведенный тип записи и неприведенный тип записи, и также важный третий тип записи — это тригонометрическая дробь единичной окружности.

Понятное дело, что типы дробей разные, но образованы по одним и тем же общим для всех правилам, по правилам общей дерадианной дроби. В этих правилах указано, что должны быть числитель и знаменатель этих дробей, а они у них у всех есть, также должна существовать некая функция пропорциональности между числителем и знаменателем, она также присутствует у всех трех дробей, эти дроби можно складывать между собой и умножать на какое-то действительное число. Поэтому эти дроби являются частным случаем более общего вида дерадианной дроби, или более общей теории дерадианных дробей, но об этом немного расскажу в следующих главах, так как эта область мной еще не в полной мере изучена, но все же какие-то зачатки уже просматриваются и заложены. Также мы еще не рассмотрели области определений и значений апофемы высоты и гипотенузы этих дробей, это мы рассмотрим также в последующей главе.

Теперь давайте рассмотрим два типа операций над дерадианными дробями — так называемые мною реверсированные операции, операции переворачивания дробей, первая операция называется реверсирование дерадианной дроби (R), и вторая операция называется транспонирование дерадианной дроби (T):

…… … (a& h) R= (h& a) = (1& 2Tan [α/2]) =

…… … … … … … … … … … = (Cot [α/2] & 2)

…… … [a& r] R= [r& a] = [1& 2Sin (α/2)] =

…… … … … … … … … … …= [Csc [α/2] & 2]

…… … {h& r} R= {r& h} = {2& Cos [α/2]} =

…… … … … …… … … … …= {2Sec [α/2] & 1}

Пример 1:

(3& 2) R= (2& 3), {3.2& 11} R= {11& 3.2},

[7& 8] R= [8& 7]

Как видим, операция реверсирования де-дроби переводит дерадианный треугольник в новый, в котором тип дерадианной дроби оставляется такой же, как и первоначальная де-дробь, над которой производилось реверсирование, но уже с новой де-дробью, у которой числитель численно равен знаменателю, а знаменатель численно равен числителю первоначальной дроби:

…… … … … … … … … 【M& N】R = 【N& M】

В транспонированной же операции де-дроби дерадианный треугольник остается тот же самый, с тем же углом при вершине, только этот угол обозначается совершенно новой дробью нового типа, называемой транспонированной дробью энного типа, и обозначаются такие дроби двойными скобочками своего типа:

…… … … … … 【M& N】 T = 【 【N& M】 】

…… … (A& H) T= ((H& A)) = ((1& 2Tan [α/2])) =

…… … … … … … … … … … = ((Cot [α/2] & 2))

…… … [A& R] T= [[R& A]] = [[1& 2Sin (α/2)]] =

…… … … … … … … … … …= [[Csc [α/2] & 2]]

…… … {H& r} T= {{R& H}} = {{2& Cos [α/2]}} =

…… … … … …… … … … …= {{2Sec [α/2] & 1}}

Пример 2:

(3& 2) T= ((2& 3)), {3.2& 11} T= {{11& 3.2}},

[7& 8] T= [[8& 7]]

Как видим, реверсирование — это просто перевернутые дерадианные дроби первых трех типов, что-то типа аналога операции транспонирования над матрицами, а транспонирование де-дробей — это уже новый тип де-дробей, что-то типа аналога своего рода обратным функциям котангенс, секанс и косеканс в тригонометрии, только не для прямоугольного треугольника, а для равнобедренного, или, что то же самое, для дерадианного треугольника, и читаются такие дроби точно так же, как и обычные дерадианные дроби, только с прилагательным: транспонированная дерадианная дробь первого типа, транспонированная дерадианная дробь второго типа и транспонированная дерадианная дробь третьего типа.

Транспонированные и обратные дроби — это не одно и то же, то есть:

…… … … (A& H) -1≠ (A& H) T, [A& R] -1 ≠ (A& R) T

…… … … … … … … … …… {H& R} -1 ≠ {H& R} T

В первом случае обозначение, забегая немного вперед, это всегда произведение прямой дроби и обратной равно единичной дроби, во втором случае при произведении прямой и транспонированной дроби единичной дроби не получается, это их основное различие, то же самое можно сказать и про операцию реверсирование:

…… … (A& H) (A& H) -1=e, (A&H) (A&H) T ≠e

…… … (A& H) (A& H) -1=e, (A&H) (A&H) R ≠e

Основные свойства транспонирования матриц не удовлетворяют основным свойствам транспонирования и реверсирования де-дробей, кроме первого:

(DL) L=D, (αD) L ≠ αDL, (D1+D2) L≠ (D1) L+ (D2) L,

(D1*D2) L≠ (D1) L (D2) L

Где, L= {R, T} — какая-то из реверсных операций, а D — какая-то дерадианная дробь из трех типов.

2.2. Эквивалентные дерадианные дроби. Сокращение дробей. Пропорция

Так как у дерадианной дроби есть сходство с обычными дробями, то вполне возможно ожидать, что у каждой приведенной дерадианной дроби также будут и эквивалентные значения отличаться только при написании, а численно будут равны приведенной, и действительно, давайте докажем это для дерадианной дроби первого типа.

Так как треугольник d (ABC) равнобедренный, см. рис. 2.2.1.

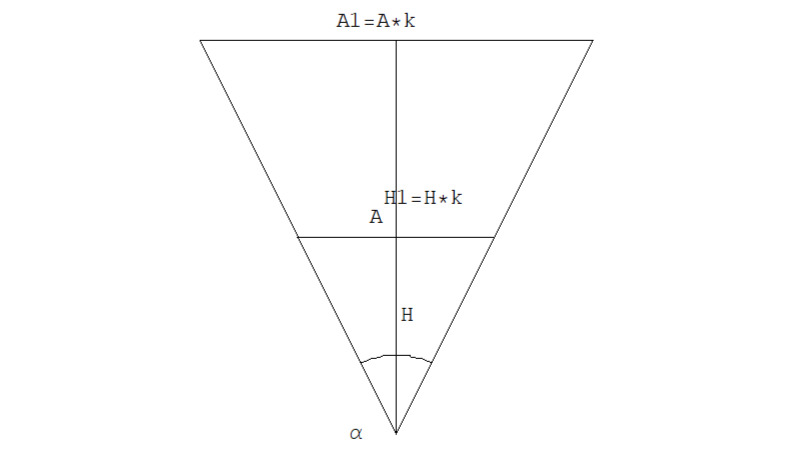
При увеличении высоты H треугольника d (ABC) в n раз получим новую высоту H1 нового треугольника d (A1B1C1), и, так как три угла треугольника d (ABC) равны трем углам треугольника d (A1B1C1), из этого следует, что треугольник d (ABC) подобен треугольнику d (A1B1C1), а из этого следует, что все их линейные размеры также увеличатся в n раз, а значит, и апофема увеличится в n раз, и поэтому можно записать: в общем виде для дерадианных дробей всех типов.

Утверждение 2.2.1

Если числитель или знаменатель дерадианной дроби увеличить (умножить) или уменьшить (разделить) в n раз, то соответствующий другой числитель или соответствующий знаменатель так же увеличится или уменьшится в n-раз. И второе: если две дерадианные дроби соответствуют одному и тому же углу, то такие дроби эквивалентны и равны между собой.

Утверждение 2.2.2

Две дерадианные дроби считаются эквивалентными и равными друг другу, если определитель составленной из их матрицы числителей и знаменателей равен нулю.

То есть, если даны две дерадианные дроби:

…… … … … … … … … ….. (A1& H1), (A2& H2) и

..…матрица… ….det [{{A1, A2}, {H1,H2}}] =0,

…то (A1& H1) ∼ (A2& H2) и (A1& H1) = (A2& H2)

Хочу обозначить, в чем разница в этой книге понятий «утверждение» и «теорема», если утверждение я могу доказывать, а могу не доказывать по собственному выбору, это зависит от очевидности утверждения или из экономии времени и места, то теорему надо обязательно доказывать, также надо понимать, что любое утверждение в этой книге имеет всегда какое-то строгое доказательство, просто я его не привожу, но оно на самом деле обязательно есть, и оно мне известно. Утверждение — это просто что-то типа не так значимой теоремы, в которой не так сильно заостряется внимание на доказательстве.

Вообще эти три утверждения очевидны, так как дерадианная дробь — это угол в дерадианном треугольнике, все линейные размеры в этом треугольнике при увеличении его одного линейного размера с одним и тем же коэффициентом подобия увеличивает так же ровно на этот коэффициент подобия и все его остальные линейные размеры и составные части. И было бы странно, если бы это было не так. Поэтому, увеличивая или уменьшая какую-то из частей {A, H, R} дерадианного треугольника в икс раз, автоматически ровно во столько же раз увеличиваются или уменьшаются и все остальные части треугольника.

…… … … … … … … {A,H,R} *x= {A*x, H*x, R*x}

Я бы сказал, что это одно из главнейших свойств дерадианных дробей — умение сокращать числитель и знаменатель, иначе это были бы не дроби, а что угодно, только не дроби.

Итак, мы рассмотрели и доказали для дроби первого типа, что при изменении апофемы в n раз пропорционально изменится и высота H в n раз, и обратно, при изменении H, также и апофема изменится (см. рис. 2.2.1), а это ровно значит, что апофема и высота в любом дерадианном треугольнике изменяются пропорционально, и мы можем апофему A и высоту H сокращать на n при n, принадлежащем к множеству вещественных чисел n∈R. И это очень похоже на сокращение обычных дробей.

Пример 4:

…… … α ≡ (6& 3) = (2*3& 1*3) = (2& 1) ≡ (π/2) r

Пример 5:

…… … … … …α ≡ (12& 8) = (3*4& 2*4) = (3& 2)

Пример 6:

….α ≡ (4/√3& 2) = (2*2/√3& 2*1) = (2/√3& 1) =

…… … …..= (2/√3*√3& 1*√3) = (2& √3) ≡ (2π/3) r

Очень интересны случаи для углов:

…… … … … … … … … … {πr, 0r}

Интересно, какие дерадианные дроби будут для этих двух значений? Давайте их найдем. Так как теперь умеем увеличивать или сокращать на одно и то же число апофему и высоту дерадианной дроби, мы можем легко найти дерадианные дроби для этих углов.

Пример 7:

…… … … …α = πr≡ (2Tan (π/2) & 1) = (2∞& 1) =

…… … … … … … … = (2 ∞⁄∞& 1⁄∞) = (2& 0) =

…… … … … … … … …= (2*1/2& 0*1/2) = (1& 0)

Для решения этого примера применим основную формулу перехода от обычного угла в радианах к дерадианной дроби (ангулярный переход) и далее решим числитель,

…… … … … … … … … … 2Tan (π/2) =2∞

после, разделив числитель и знаменатель дерадианной дроби на бесконечность, тем самым сократив на одно и то же число или символ, придем к дроби:

…… … … … … … … … … (2& 0)

и, снова сократив обе части дерадианной дроби — апофему и высоту — на 2, придем к конечному результату — к

несократимой дерадианной дроби (1& 0).

Предостережение

В дерадианной дроби нельзя одновременно умножать числитель и знаменатель на 0, потому что получится дробь вида (0& 0), а это дробь неопределенная (или, как я ее считаю, геометрическая дробь точки центра окружности)

Это действие — умножение числителя и знаменателя на ноль — то же самое, что делить на ноль действительное число, и будем в дальнейшем считать «запрещенным» действием (но не всегда, могут быть и встречаться и очень особые случаи, почти парадоксальные, где без этого действия никак не обойтись).

Пример 8:

α = 0r ≡ (2Tan (0/2) & 1) = (2*0& 1) = (0& 1)

И для второго угла мы сделаем все то же самое, что и в примере 7, а именно: найдем числитель дерадианной дроби, он равен нулю, и далее еще раз найдем, что:

…… … … … … … … … … 0r≡ (0& 1)

И тут также видно, что из дерадианной дроби:

(0& 1), если апофема равна нулю, то высота аналогично может равняться любому значению, например (0& a), и, всегда сократив на а, получим приведенную несократимую дробь (0& 1).

Какой можно важный вывод из последних двух примеров сделать:

0r≡ (0& a) = (0& 1), πr≡ (a& 0) = (1& 0)

при любом значении a. Также интересно, какие краевые (в смысле с краев) значения будут для двух других типов дробей, давайте также найдем их. Сначала найдем для угла 0r:

…… … … … … … …0r≡ (2Tan [0/2] & 1) = (0& 1)

…… … … … … … …0r≡ [2Sin [0/2] & 1] = [0& 1]

…… … … … … … …..0r≡ {2Cos [0/2] & 2} = {1& 1}

Теперь найдем для πr:

…… … … … … … … πr≡ (2Tan [π/2] & 1) = (1& 0)

…… … … … … … … πr≡ [2Sin [π/2] & 1] = [2& 1]

…… … … … … … … πr≡ {2Cos [π/2] & 2} = {0& 1}

И выпишем в таблицу см. рис. 2.2.2 и в дальнейшем будем ей часто пользоваться при решении задач:

Далее целесообразно было бы ввести определение несократимой дерадианной дроби.

Определение 2.2.1

Дерадианная дробь называется несократимой, если (как в случае и с обычными дробями) числитель и знаменатель дерадианной дроби — натуральные числа и взаимно просты, т. е.

НОД (M, N) =1, где M — это числитель дерад. дроби, а N — знаменатель дерад. дроби.

Например,

…… … … … (3& 1), {2& 7}, [11& 9], (53& 23),…

Теперь давайте разберем такую важную тему, как пропорции, так как без них просто немыслима математика вообще, то дерадианные дроби — это, по сути, и есть уже готовые пропорции, которые, чтобы составить, надо просто перемножить накрест числители и знаменатели.

Утверждение 2.2.1

Если даны две равные и пропорциональные дерадианные дроби, такие, что

【 M1& N1 】 = 【 M2& N2 】, то из них всегда можно из их числителей и знаменателей составить пропорцию:

M1*N2 = M2*N1.

Это правило или утверждение будет касаться любых типов дробей. Доказательство этого утверждения нисколько не сложное. См. рис. 2.2.3.

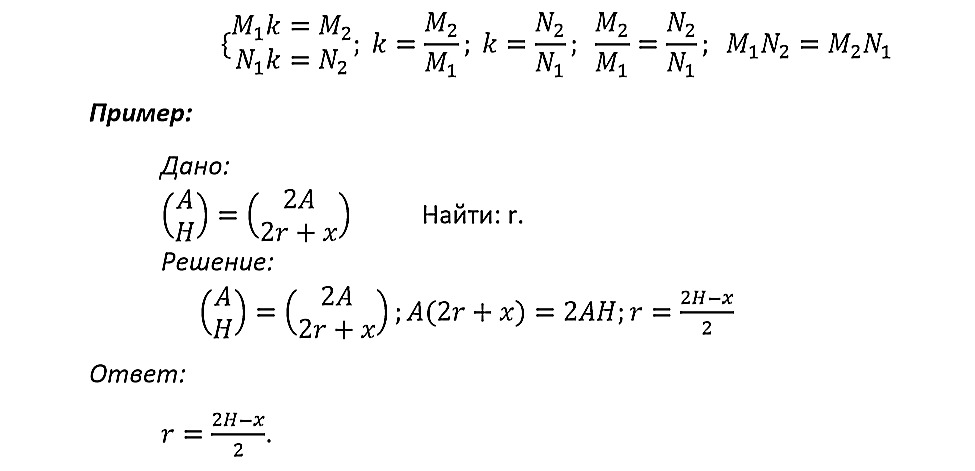
Следствие

Если даны равные друг другу любой природы функции:

g [x] =q [x], то всегда будет выполняться такое тождество:

…… … … (1& 1) = (g [x] & q [x]) = (q [x] & g [x])

Например, мы знаем уравнение для золотого сечения: см. рис. 2.2.4.

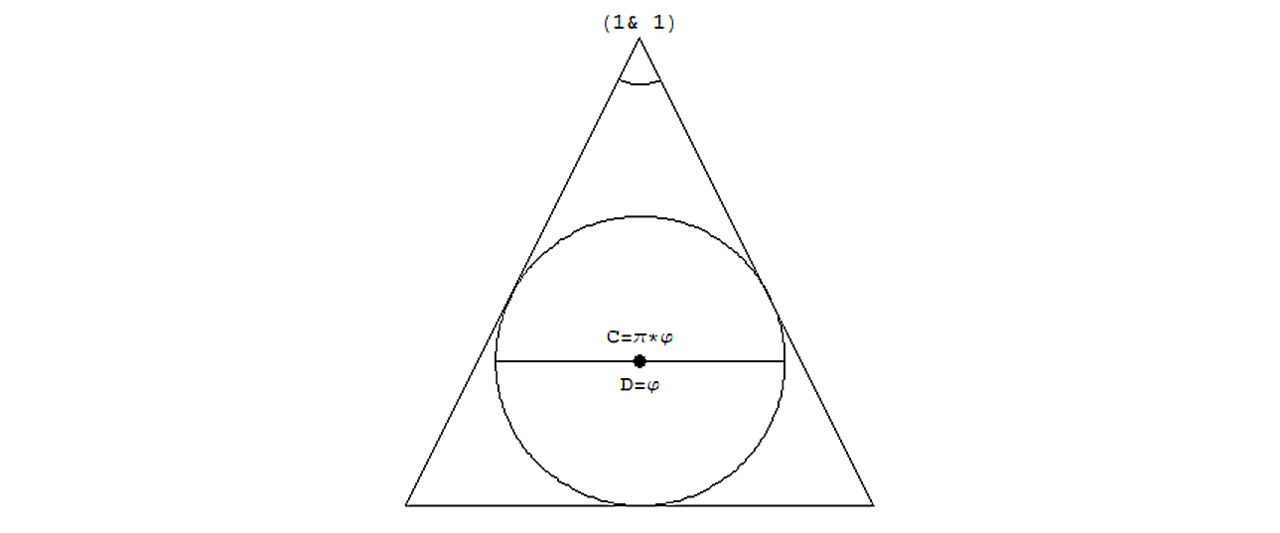
Также расскажу про φ-золотое сечение, есть другой интересный факт, связанный с дерадианным углом или дробью (1& 1), установленный когда-то давно мной: если взять окружность с диаметром, равным ровно золотому сечению, то такая окружность всегда будет вписываться в правильный дерадианный треугольник с вершиной (1& 1), а длина данной окружности будет равна С=π*φ, как видим, налицо связь, и связывает эти две постоянные дерадианный угол в один дерадиан. См. рис. 2.2.5.

2.3. Таблицы дерадианных дробей для распространенных углов

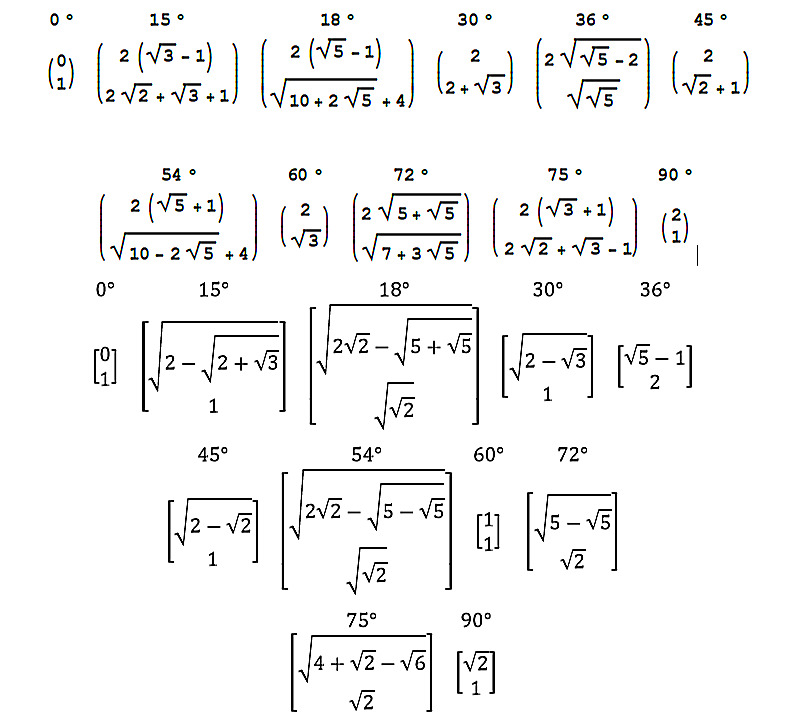
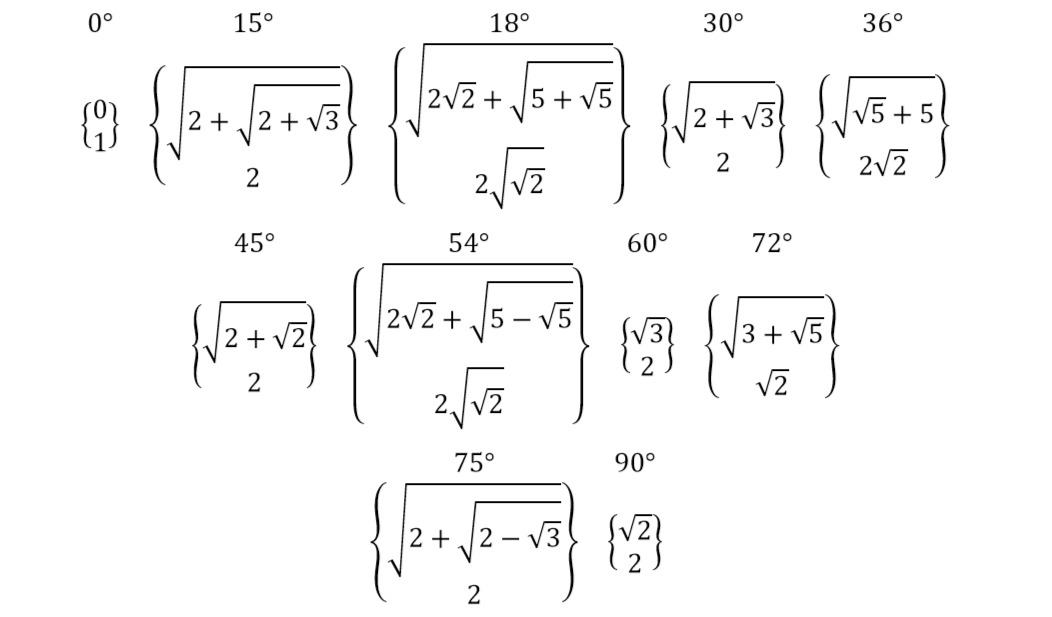
Такие углы нас будут мало интересовать, только как примеры и при решении некоторых задач, все потому что они очень хорошо представлены в современной геометрии и тригонометрии, а в основном мы будем изучать углы чисто дерадианной природы, малоизученной, и которые просто в современной геометрии даже не рассматриваются и никак не представлены из-за своей либо трансцендентности, либо неприменимости на практике, также будем рассматривать, в общем, все, что связано с дерадианной арифметикой, тригонометрией и геометрией вообще.

2.4. Скалярный вид дерадианного угла, или Обратная формула перехода от дерадианного угла к обычному. Десятичная запись д/д. Периодические д/дроби. Сопряженные гипотенуза и высота

На практике при решении задач и изучении каких-то свойств дробей может иногда быть так, что нам дан сам дерадианный угол, а нам надо по нему найти обычный угол и выразить его в радианах или градусах. Для этого можно воспользоваться обратной формулой перехода от дерадианного угла n-го типа к обычному. И выглядят эти формулы так (см. рис. 2.4.1):

Обратите внимание на обозначение скалярного вида угла, пишется в своих скобочках через дробь.

Доказательство

Давайте докажем их по порядку, см. рис. 2.4.2.

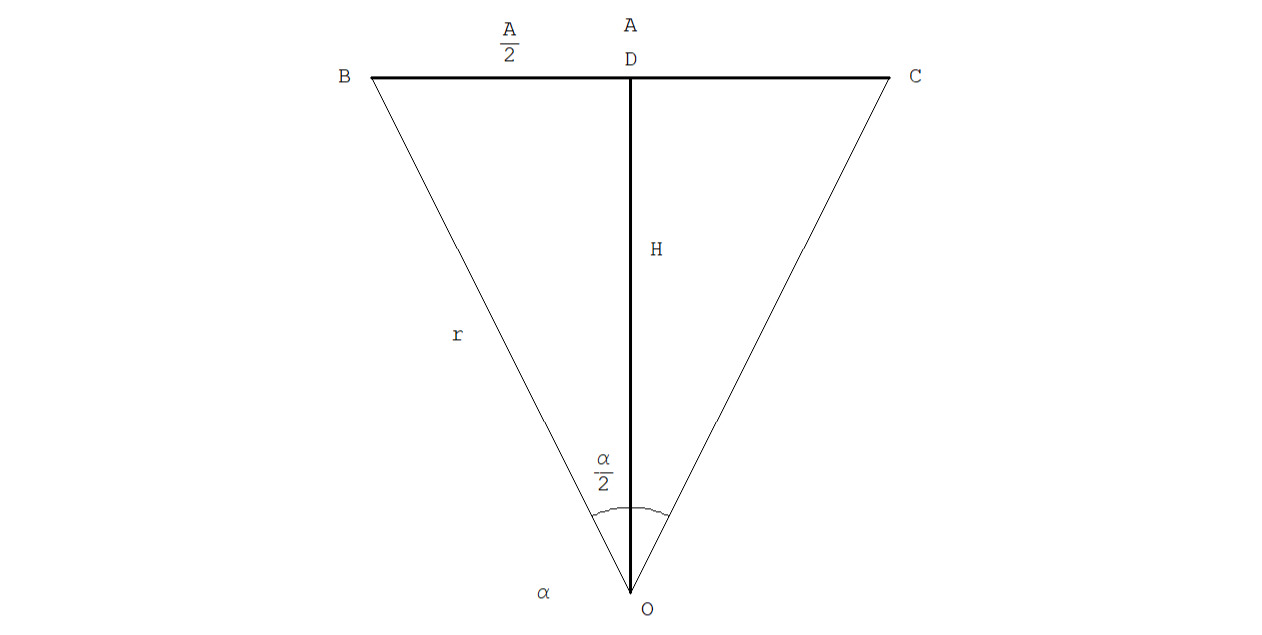
Если поделить дерадианный треугольник на два равных прямоугольных треугольника (я их называю половинными дерадианными треугольниками) и рассмотреть один из них, любой, тогда его катеты будут равняться: противолежащий A/2, прилежащий катет будет равняться апофеме H, и прямоугольный треугольник {{}} OBD с углом α/2, и т. к. это половина дерадианного угла, тогда тангенс этого угла прямоугольного треугольника будет равен отношению противоположного катета к прилежащему, а именно:

…… … Tan (α/2) = (A⁄2) /H, α=2ArcTan (A/2H),

откуда уже совсем все становится очевидным, если тангенс перенести в правую часть, поменяв на противоположную функцию арктангенс, и умножив обе части на 2, придем к выражению 2.4.1, что и требовалось доказать. Для остальных дробей все будет то же самое. Только уже будет находиться скалярный вид дробей через синус и косинус половинного угла, см. рис. 2.4.3.

Не стоит путать эти две записи: скалярное значение и действительное значение дерадианной дроби, — численно они различны, действительная запись дерадианной дроби равна так называемой записи приведенной функции числителя T (x), см. главу 3.2. Для остальных типов дробей все то же самое есть и действительный вид и скалярный вид. При сложении-вычитании десятичных записей дробей их сумма-разность не равны сумме-разности их дерадианных дробей, это надо помнить:

…… … (1& 2) + (2& 3) = (14& 11) ≠1/2+2/3=7/6

…… …. ….… … ….….… …. (14& 11) =14/11≠7/6

А вот сумма и разность скалярного вида на вид одинаковы:

…… …. ….… … …. … … (1& 2) + (2& 3) = (14& 11)

…… …. ….… … ….….….. … (1/2) + (2/3) = (14/11)

А вот если две различные дроби имеют одну и ту же десятичную дробь, то это значит, что эти две дерадианные дроби равны и эквивалентны:

…… …. ….… (a& h) = (a1& h1), если a/h=a1/h1

Дорогой читатель, не пугайтесь названий, названия придуманы сугубо мной лично, название взято только потому, что любую дерадианную дробь всегда можно выразить одним-единственным действительным числом, а, как мы знаем, любое вещественное число — это скаляр. Отсюда и такое название — скалярный вид угла, то есть когда угол задается одним-единственным числом и всегда в радианах.

Иногда формулы 2.4.1 и остальные удобно использовать для проверки правильности дерадианных дробей, например, зная обычный угол, и нашли для него какую дерадианную дробь, но не знаем, правильно ли мы ее нашли, тогда можно подставить в эту формулу вместо {A, H, R} найденные значения и сравнить ответ с известным углом, если они совпадают, значит, мы дерадианную дробь нашли верно.

Пример:

Дан угол 30°, и мы нашли для него какую-то дерадианную дробь.

…… …. ….… … … … … … … … … … (2& 2+√3)

Требуется узнать, правильно ли мы для этого угла нашли эту дробь.

Возьмем апофему и высоту найденной дерадианной дроби и подставим в формулу 2.4.1:

……. (2/ (2+√3) =2ArcTan [2/2 (2+√3)] = (π/6) r=30°

И убеждаемся, что ответ совпадает с изначальным углом, значит, дерадианную дробь мы нашли верно. Ну и также еще хотелось бы отметить, если повнимательнее присмотреться к формуле 2.4.1, то хорошо видно, что это на самом деле тангенс половинного угла, выраженный через апофему и высоту. Пока просто запомним ее, в будущем она нам еще не раз пригодится:

…… … … … … … … … … … … …Tan [α/2] =A/ (2H)

Во всех трех случаях нам встречаются тригонометрические функции половинных углов. Хорошо бы их тоже запомнить. В дальнейшем мы еще к ним не раз вернемся, когда будем изучать функции пропорциональности числителя и знаменателя T (x) и CT (x). А пока их выпишем и запомним:

…… ….… …Tan [α/2] =A/ (2H), Sin [α/2] =A/ (2R),

…… … … … … … … … … … … ...Cos [α/2] =H/R

Теорема

(A/H) = [A/R] = {H/R} =⋯=Lα/Rf = (2Sα) /Rf2

Где Lα — длина дуги сектора c центральным углом α. Скалярный тип всех трех типов углов равны и равны длине дуги сектора, деленной на Rf — фактическую, или истинную, гипотенузу его дерадианного угла. Sα — площадь сектора.

См. рис. 2.4.4.

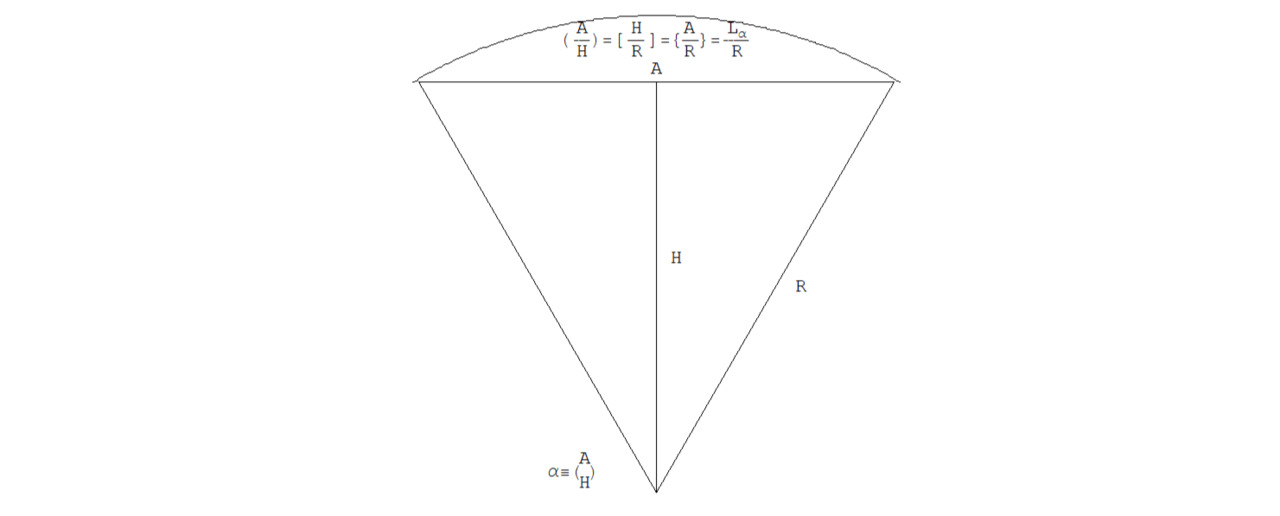
То, что эти скалярные дроби равны друг другу, это вполне очевидно и понятно, так как они равны одному и тому же углу. Давайте найдем длину дуги сектора угла альфа — α.

См. рис. 2.4.5.

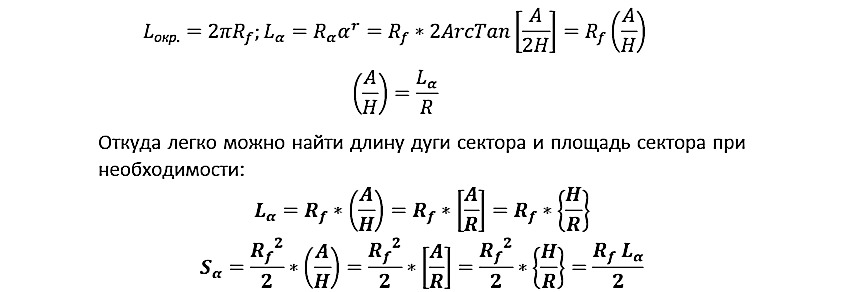
Например, см. рис. 2.4.6.

Из этих примеров хорошо видно, что с помощью обычной тригонометрии удобно работать с обычными треугольниками, а с помощью дерадианной тригонометрии или теории удобно работать с окружностями и секторами, а также, как видим, длина апофемы и «радиал» (длина дуги сектора, мой термин, производное от «радикал») — это всегда обратные величины, как наподобие обратных функции, например, функций синус и арксинус — это как бы и есть основной геометрический смысл и связь дерадианной дроби и ее скалярной величины.

…… … … … … … … … … … A=H*2Tan (α/2) *R,

…… … … …Lα= (A/H) *R=2 ArcTan (A/ (2 H)) *R

Определение

Выражения типа

…… … … … R┴=√ (4H2-A2), H┴=√ (4R2-A2)

называются сопряженной гипотенузой к гипотенузе R, а также, соответственно, сопряженной высотой к высоте H:

…… … … …..R=√ (4H2+A2), H=√ (4R2+A2)

Еще иногда буду называть для простоты гипотенузу R радиус-вектором, наподобие как называется в линейной или векторной алгебре радиус-вектор. Это очень удобное обозначение гипотенузы и высоты, не надо постоянно писать корни, так как эти формулы часто встречается в формулах, например:

…… … … ….. R┴ /R=√ Tan [(A& H)]

…… … … ….. 2 (A& H) = (4AH& R┴2)

…… … … ….. [A& R] ≡ (2A& H┴) ≡ {H┴& 2R}

…… … … ….. {H& R} ≡ (2H┴& H) ≡ [2 H┴& R]

…… … … ….. SΔ=AH/2= (AH┴) /4, ……

* (Для лучшего запоминания некоторых формул я использую треугольник такого типа {A, H, R}:

…… … … ….… … … … {4H ┴, H ┴, R} =

…… … = {4√ (R2-H2), √ (4R2-A2), √ (4H2+A2)})

Сопряженная гипотенуза и сопряженная высота — это просто значит геометрически гипотенуза или высота, зеркально симметричная относительно оси ОХ аналогия с комплексными числами. Эти понятия часто еще будут встречаться в дальнейшем, поэтому эти понятия надо сразу как-то обозначить и ввести в оборот нашей речи. Также возможны и такого рода соотношения:

(Abs [(H2) ┴- (R2) ┴]) / (abs [H2-R2]) =4

Свойства сопряженных дерадианных величин:

(Sn) ┴= (S┴) n

α (S┴) = (αS) ┴

Теперь вернемся опять к скалярному виду де-дроби, хочу отметить, что скалярный вид дроби — это не совсем обратный угол дерадианной дроби, так как скалярный вид угла не учитывает периодичности угла, например, (1& 1) *7= (29& 139), этот угол больше 360° градусов, и мы бы его должны были записать как-то по-другому, а именно: учитывать, что угол α, и такой же, но периодический угол α+2πn — это не один и тот же угол, это только для тригонометрических функций эти значения одно и то же значат, а так как мы все решаем через тригонометрические функции, то и периодичность никак не отображается для одних и тех же периодических углов, давайте докажем, что все периодические углы будут в дерадианных терминах записываться одинаково. Допустим, нам дан какой-то угол α, тогда его периодический угол будет выглядеть как α+2πn, тогда сделаем ангулярный переход (см. гл. 4.6) к дерадианным дробям и запишем это выражение через соответствующие дроби:

…… … … α+2πn ≡ (2Tan [α/2] & 1) +2* (1& 0) n=

…= (2Tan [α/2] & 1) + (0& 1) n = (2Tan [α/2] & 1)

То есть периодический угол в дерадианной форме никак не зависит от периода, или все углы с периодом 2πn в де-форме будут записываться одинаково, а значит, дроби всех периодических углов будут между собой равны, а сами углы эквивалентны, если мы только как-то специально не введем новое обозначение для таких периодических углов. Например, угол:

…… … … … … … … … … 30°≡390°≡750°≡…≡

…..… … … … ≡ (2 (2-√3) & 1) = (2 (2-√3) /1)

И, соответственно, и скалярный вид таких эквивалентных углов будет между собой равным. Но это и понятно, так как графически у всех этих углов периодических будут одни и те же апофема и высота.

2.5. Несоизмеримость

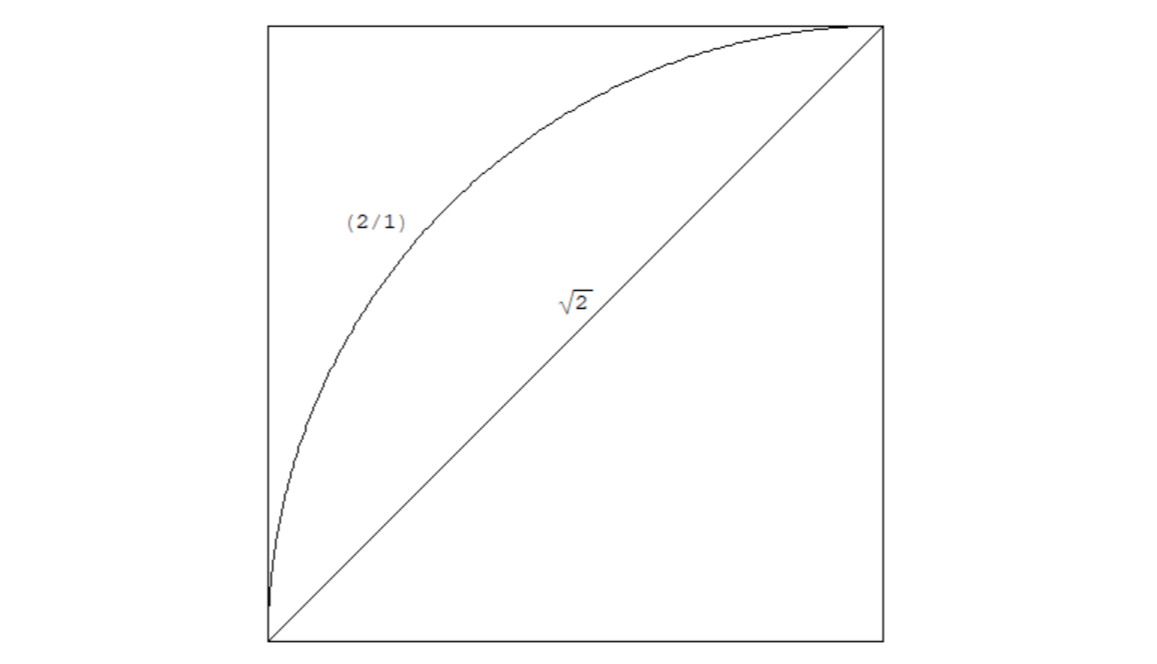
В этой главе я хочу рассказать о новой величине, о которой все знают, но не подозревают, которая точно так же несоизмерима, только уже не только со стороной квадрата, но и с диагональю квадрата, а именно ни с 1, и ни с √2, а выглядит эта величина так: (2/1), — эта величина — это длина части окружности радиуса единицы (в моих терминах — радиал) и углом сектора, равным π/2, см. рис 2.5.1, и правда, давайте это предположение или высказывание докажем:

…… … … … … … … (2/1) =2ArcTan [2/ (2*1)] =π/2

Эта величина равна π/2, а как мы знаем еще со школы, что число π трансцендентно, а это и значит, что оно несоизмеримо ни с каким алгебраическим числом и ни с каким тем более целым, то есть это число нельзя записать в виде конечной формулы, используя конечное число операций только сложения, умножения, деления над любыми алгебраическими и целыми числами. Раз мы нашли такую несоизмеримую величину, и она является действительным числом, то тогда, возможно, существуют и другие подобные значения, пожалуйста, вот примеры — сколько угодно таких величин:

…… … … … … … … … (1/1), (3/5), (7/8), (9/7),…

Как видим, это новый класс величин, или, что то же самое, новый класс чисел, который я называю множеством рациональных дерадианных дробей, а точнее, множеством дерадианных рациональных чисел, и поэтому к данным «новым числам» надо относиться точно так же, как и к другим уникальным множествам типа рациональных чисел, целых чисел, отрицательных и т. д. Так как они нам расширяют горизонты и дают возможность новых вычислений и лучшего понимания природы числа, а также эта каждая дробь (несократимая) образует свою собственную тригонометрию, в которую входят и выражаются углы только через базисный угол (неделимый рациональный угол) этой тригонометрии и который является постоянной этой тригонометрии, точно так же как число Пи является базисным углом в радианной геометрии: G1,0=G2,1

…… … … … … γ 1,0 =2ArcTan [1/ (2*0)] =π ≡180°

В тригонометрии G1,0, хорошо измерять углы типа π*q,q∈ℚ, но если углы другой природы, например: γ 1,1*q∈ℚ, то это не совсем, как по мне, становится удобно, и тогда стоит использовать другую тригонометрию, более подходящую для нее, а на сегодняшний день мы пытаемся измерять углы все только через константу Пи, а это может быть не совсем всегда удобно, а порой и вовсе невозможно, и дальше мы попытаемся решить этот вопрос с помощью независимых положительных рациональных тригонометрий: Gn, m, где n,m∈ℕ

2.6. Умножение деление угла на число: c=const. Возведение в степень и обратную степень. Вынесение множителя из-под дроби. Функция пропорциональности

Пока что мы наблюдаем некоторую алгебраическую похожесть всех трех типов дробей, то есть внутреннюю одинаковую природу, интересно, как они будут себя вести при других операциях, например, умножении на число, просто сложении и так далее. Но мы еще не обговорили, что такое умножение и сложение дерадианных дробей. А умножений на число существует аж два типа.

Утверждение 2.6.1

Если умножить угол α на число c=const, то тогда числитель и знаменатель дроби одновременно умножатся на это число, то есть:

…… … … … … … … … … c× (A& H) = (c*A& c*H)

…… … … … … … … … … c× [A& R)] = [c*A& c*R]

…… … … … … … … … … c× {H& R} = {c*H& c*R}

и такое произведение называется прямым произведением дерадианной дроби на число с=const.

Геометрически это просто наш дерадианный треугольник, его апофема, высота и гипотенуза увеличатся в c раз.

Сразу приведу параллель с комплексными числами: данной операции алгебраически и геометрически соответствует операция умножения комплексного числа на константу.

…… … … … … … … … … x* (a±b*ⅈ) =x*a±x*bⅈ

Такое сравнение и параллель, пожалуй, будут самыми уместными в данном случае. Как видим, и действительная, и мнимая части умножаются по отдельности по закону распределительному (дистрибутивности) умножения, и я не зря привожу эту аналогию, в дальнейшем вы сами все увидите и поймете почему, и даже, возможно, немного удивитесь.

Утверждение 2.6.2

Если разделить угол α на число c = const, и тогда числитель и знаменатель дроби одновременно разделятся на это число, то есть

…… … … … … … … … … (A& H):с= (A/c& H/c)

…… … … … … … … … … [A& R)]:c= [A/c& R/c]

…… … … … … … … … … {H& R)}:c= {H/c& R/c}

И такое произведение называется прямым отношением или прямым делением дерадианной дроби на число с = const.

Геометрически это просто наш дерадианный треугольник, его апофема, высота и гипотенуза уменьшатся в c раз, и это геометрически и алгебраически соответствует отношению комплексного числа к числу x = const.

…… … … … … … … … … (a±b*ⅈ) /x=a/x±bⅈ/x

Утверждение 2.6.3

Если умножить угол α на число c=const, то тогда аргумент функции числителя дерадианной дроби также умножится на число c, то есть

с*α≡ с* (2Tan [α/2] & 1) = (2Tan [c*α/2] & 1),cϵR

Или в общем виде для всех трех типов дробей

…… … … … … … … … …c*x≡ 【 F [c*x] & 1 】, c*x ϵ R

F [x] — какая-то тригонометрическая функция пропорциональности одной из дерадианных дробей типа n.

Само такое произведение называется степенным произведением дерадианной дроби на число c = const.

Как видим, мы рассмотрели два разных типа произведения (в силу свойства дистрибутивности операций) на число с, первое называется мной прямым, или линейным, произведением на число, а второе называется степенным произведением на число.

Вы, возможно, спросите почему «степенным», а все дело в том, что данному произведению соответствует комплексное число, взятое в какую-то натуральную степень n = const, например:

…… … … … (a+b*ⅈ) 3=a3—3ab2+3ⅈa2*b-ⅈb3

ровно поэтому и степенным — все из-за соответствия комплексным числам, надо это сразу понимать, так как мы не возводим в степень, а умножаем, то прилагательное просто показывает, что эта операция не чисто умножение на число, а по совместительству и возведение в степень. То есть геометрически результат ведет себя одновременно и как умножение на число, и как возведение в степень. Давайте поясню это: при возведении в степень комплексного числа радиус-вектор поворачивается на какой-то угол относительно начала координат, так вот при умножении дерадианной дроби гипотенуза так же поворачивается относительно начала координат на какой-то угол, но при этом алгебраически нам надо было бы обозначить эту операцию по аналогии с комплексными числами операцией возведения в степень, но в дальнейшем мы убедимся, что это и операция как бы умножения, и операция возведения в степень. И такая двойственность будет с этими дробями встречаться повсюду. Также обратите внимание, что я использую два разных символа умножения на число: «×» и «*», — дабы различать две этих операции.

Ну это и понятно, так как x при умножении остается все так же углом, а основная формула для дерадианной дроби верна для любого угла. Например, для более хорошей наглядности я буду использовать градусную меру. И все примеры и доказательства буду проводить и приводить только для дерадианной дроби первого типа, для остальных дробей все будет то же самое, буду просто выписывать конечный результат для экономии вашего времени и текста.

См. рис. 2.6.1.

Такие же примеры можно составить и для транспонированных де-дробей. Например, давайте докажем эту теорему геометрически для дроби первого типа как частный случай. Доказывать будем через теорему косинусов, для этого, так как мы ищем дерадианную дробь для угла с*α, то для этого нам надо найти апофему угла с*α и высоту. По теореме косинусов апофема A=AC будет равна — см. рис 2.6.2.

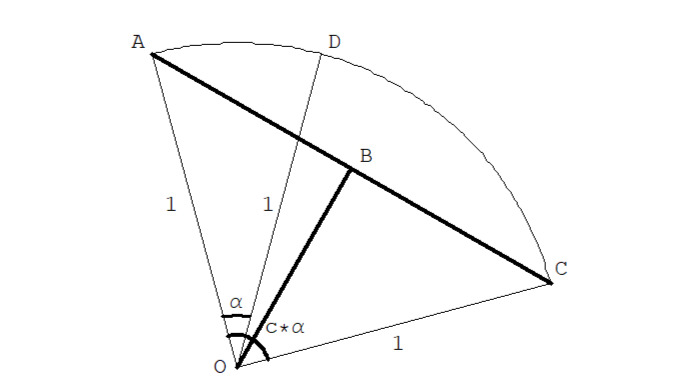
AC=A= √ (12+12+2*1*Cos (α*c))

а высота H=OB.

OB=H= √ (12- (AC/2) 2) =

= √ (1—2 (1-Cos (α*c)) /4) =

= √ (2—1+Cos (α*c)) /2) = √ (1+Cos (α*c)) / √ 2

Подставив в дерадианную дробь и преобразовав, получим:

c*α ≡ (A& H) = (AC& OD) =

= (√2 √ (1-Cos (α*c)) & √ (1+Cos (α*c)) / √2) =

= (2 √ (1-Cos (α*c)) & √ (1+Cos (α*c)))

Далее, если вспомнить формулы из тригонометрии для синуса и косинуса половинного угла и немного преобразовав эти формулы к нужному виду, как нам надо:

…… … … … …Sin (α/2) =± √ (1-Cos (α/2) / √2

…… … … … … Cos (α/2) =± √ (1+Cos (α/2) / √2

Просто перенеся квадратный корень из двух в левую часть, то есть умножив обе части на квадратный корень и подставив в дерадианную дробь, тем самым упростим ее, получим:

с* α ≡ (2 √ (1-Cos (α*c)) & 2√ (1+Cos (α*c))) =

= (2√ 2 Sin (α/2*c) & √ 2 Cos (α/2*c)) =

= (2Tan (α/2) & 1)

Что и требовалось доказать.

Понятно, что если мы можем умножать, то и делить так же можем на число, для этого достаточно умножить на 1/c, и мы можем умножение заменить на деление.

А это значит, что:

α⁄c≡1/c* (2Tan [α/2] & 1) = (2Tan [1/c*α/2] & 1) =

= (2Tan [α/2c] & 1),cϵR

Если разделить угол α на число cϵℝ, то тогда аргумент при тангенсе числителя дерадианной дроби также разделится на число c, то есть:

…… … … …α⁄c≡ (2Tan [α/ (2c)] & 1), при c=const

Также хочется добавить одно свойство, что умножать на число угол альфа можно как справа, так и слева, то есть умножение на константу дерадианного угла коммутативно, то есть:

…… … … … … … … … … c * (M& N) = (M& N) *c

Так как операция умножения действует на аргумент по правилам обычного умножения, а обычная операция умножения коммутативна в таких случаях. А теперь давайте рассмотрим эту теорему в более общем смысле.

Для того чтобы не писать для каждого типа дроби и каждый раз проводить доказательство отдельно, мы введем понятие общего вида дерадианной дроби, чтобы не повторяться и не писать одно и то же по много раз, в дальнейшем доказательство каких-то общих теорем будем проводить над этой общей формулой.

Определение

Общая дерадианная дробь — это дробь вида (приведенная), выражающая переменную величину ξ-кси, в виде дерадианной дроби:

…… … … … … … … ξ≡ (M& N), ξ≡ (F (ξ) & 1),

где два параметра M, N — это числитель и знаменатель дроби, оба зависят от переменной ξ-кси, или

…… … … … … … … … … … … M= μ (ξ), N=η (ξ)

F (ξ) =M/N= (μ (ξ) / (η (ξ) — функция пропорциональности числителя и знаменателя дерадианной дроби.

И читается как «кси соответствует: эф кси к одному».

Если F (ξ) -функция раскладывается на отношение двух функций и это отношение несократимо, то тогда дробь можно записать в таком виде:

если F (ξ) =μ (ξ) /η (ξ) и (μ (ξ),η (ξ) =1, то тогда ξ≡ (μ (ξ) & η (ξ))

Теорема 2.6.1

(теорема о композиции (или о подстановке))

Если ξ≡ (F [ξ] & 1), где (F [ξ] & 1) — общая дерадианная дробь,

ξ — переменная величина, которую выражает эта дробь, а

F [ξ] — функция пропорциональности величины ξ и {ξ, f (ξ)} {{}} {{}} {{}}, то

…… … … … … … … … … … … f (ξ) ≡ (F [f (ξ)] & 1)

Это значит, что какие бы мы операции и преобразования над величиной кси ξ ни производили (лишь бы только угол не переставал после действия на него функции принадлежать тому же самому множеству, которому принадлежал изначально, и область определения функции f (ξ) не выходила за границы первоначального множества вещественных чисел), те же операции и преобразования будут производится и над аргументом функции числителя дерадианной дроби данного угла. По сути, это преобразование называется композицией функций, когда мы одну функцию вкладываем, отображаем в аргумент другой функции.

Доказательство

Так как углы α и f (ξ) принадлежат одному и тому же множеству R, а F [ξ] формула для дерадианного угла верна для любого элемента этого множества, хоть для ξ, хоть для f (ξ), мы просто спокойно можем на этом основании заменить ξ на f (ξ), отсюда и следует истинность теоремы о композиции.

Пример для первого типа:

…… … … … … … … α+β ≡ (2Tan ((α+β) /2) & 1)

Если представить f [x] =α+x, где x — это какой-то угол бета β. То для этой функции угол x после преобразований f [x] все так же остается углом, так как {α, β, α+β} ∈ℝ, поэтому мы можем f [x] =α+x подставить в половинный аргумент числителя и найти дерадианную дробь для данной функции f [x] =α+x.

Эта же теорема о подстановке действует и для всех остальных дерадианных дробей всех типов. В дальнейшем нам эта теорема нужна будет для доказательства других теорем, связанных с элементарными преобразованиями угла. Общее правило для общей дерадианной дроби будет из всего выше сказанного таким:

В дальнейшем местами буду приводить примеры, а теоремы доказывать только для общего вида дерадианной дроби, и как в пример приводить первый тип дроби для экономии времени и места. Это значит, что с остальными дерадианными типами углов будет происходить все то же самое, только лишь численные результаты будут немного разные, а сами преобразования будут теми же самыми.

…… … … … … … … … … с*α≡ (2Tan [α/2*c] & 1) ≡

…… … … … ≡ [2Sin [α/2*c] & 1] ≡ {Cos [α/2*c] & 1}

Это исходит из общей теоремы о подстановке.

Эта формула работает в обе стороны, то есть можно как заносить c в числитель аргумента дерадианной дроби, так и наоборот, выносить из числителя аргумента, это бывает иногда очень полезно.

Вообще, забегая вперед, теорема подстановки — это одна из главных теорем теории дерадианных дробей, с помощью нее в следующих главах легко доказываются сложные арифметические и алгебраические выражения. Несмотря на свою простоту и очевидность, это очень хорошая, полезная и сильная теорема для данной теории!

2.7. Геометрический смысл основной формулы перехода

Давайте еще раз вернемся к основной формуле перехода и рассмотрим ее геометрический смысл на тригонометрической единичной окружности для всех основных типов дробей: см. рис.2.7.1. Начнем с первого типа дроби. Как мы знаем из тригонометрии школьного курса, радиус такой окружности равен единице, а катеты равны синус угла альфа и косинус угла альфа, тогда из чертежа видно, что углу два альфа будет соответствовать дерадианная дробь:

…… … … … … … … … … 2α≡ (2Sin (α) & Cos (α))

— тригонометрическая форма записи дерадианного двойного угла первого типа (см. рис.2.7.1).

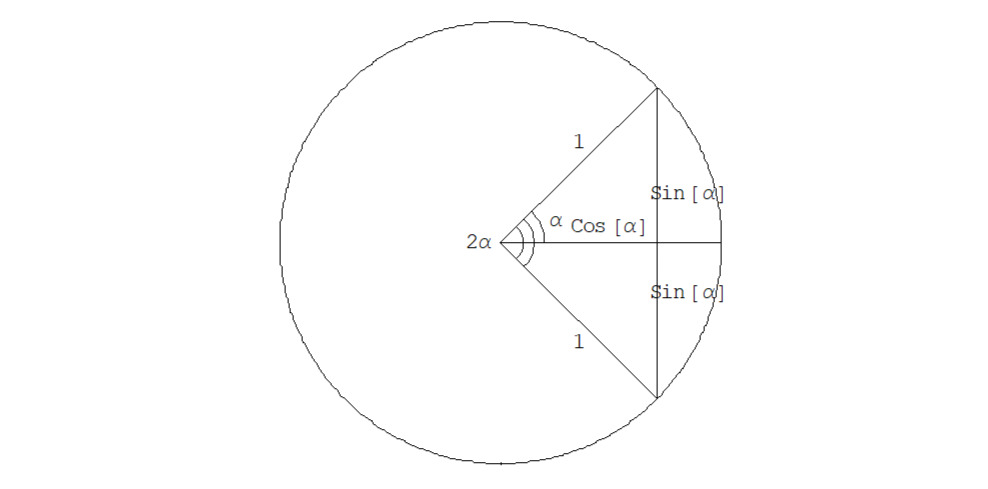
И если разделить и сократить числитель и знаменатель на одно и то же число Cos () и упростить выражение (мы ведь это всегда можем сделать, см. параграф 2.2), то получим:

…… … … … … … … … … 2α ≡ (2Tan (α) & 1)

Далее, умножив обе части на 1/2 (на число мы также умеем умножать, см. параграф 2.6) и опять упростив, в конце концов получим то же самое тождество, что и в параграфе 2.1 — формулу основного перехода для дроби первого типа от плоского угла к дерадианной дроби. Такое решение и будем называть геометрическим смыслом основной формулы перехода для дроби первого типа. См. рис. 2.7.1.

…… … … … … …..2α *1/2 ≡ 1/2* (2 Tan (α) & 1) =

…… … … … … ….. … … …..= (2Tan (α/2) & 1) ≡ α

Для остальных двух основных тригонометрических дробей давайте также рассмотрим, для дроби второго типа из рисунка 2.7.1 составим дробь:

……2α≡ [2Sin [α] & 1] …2α*1/2≡ [2Sin [α*1/2] & 1]

…… … … … … … … … … … … α≡ [2Sin [α/2] & 1)]

И для третьей дроби будет, главное помнить, что мы выражаем углы через:

…… … … … …… α≡ (A& H) ≡ [A& R] ≡ {H& R}

…2α≡ {Cos [α] & 1} … 2α*1/2≡ {Cos [α*1/2] & 1}

…… … … α≡ {Cos [α/2] & 1} = {2Cos [α/2] & 2}

Геометрический смысл дает хорошее наглядное представление из тригонометрической окружности (числовая окружность в моих терминах), как надо работать с дерадианными углами.

Задача 1

Дан ромб с диагоналями 2 и 3. Напротив угла альфа лежит диагональ длины 2, а напротив угла бета лежит диагональ длины 3. Найти дерадианные дроби для углов альфа и бета.

См. рис. 2.7.2.

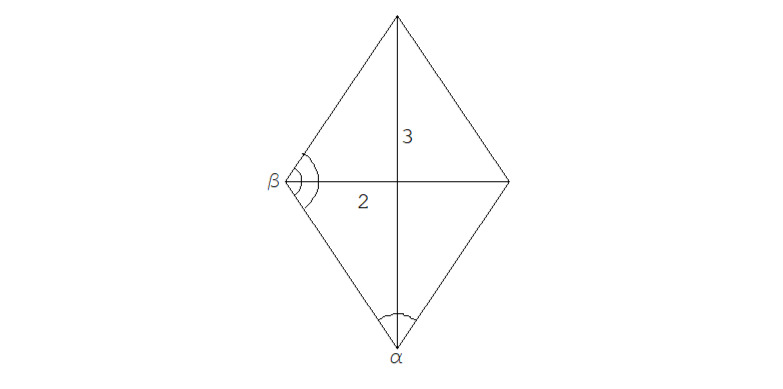
Вспомним определение дерадианного угла — это пара двух значений апофемы А и высоты H. Тогда для углов альфа и бета, исходя из основного определения, дерадианный угол будет:

α ≡ (2& 3/2) = (2*2& 3/2*2) = (4& 3)

β ≡ (3& 2/2) = (3& 1)

Ответ: α ≡ (4& 3), β ≡ (3& 1)

Задача 2

Перевести углы альфа и бета из задачи 1 в обычные углы в градусах.

α≡ (4& 3) ≡ (4/3) =2ArcTan [4/ (2*3)] =67.3801…°

β≡ (3& 1) ≡ (3/1) =2ArcTan [3/ (2*1)] =112.6019…°

Ответ: {{}} {} {{}} α=67.3801…° … β=112.6019…°

Задача 3

Дан ромб со стороной, равной 3, и напротив угла альфа лежит диагональ длины 5. Найти дерадианные дроби для углов альфа и бета.

Выразим сначала угол альфа через дробь второго типа, так как нам дана гипотенуза R=3 и апофема A=5 этого угла: α≡ [5& 3], далее найдем вторую диагональ: d2=2√ (32- (5/2) 2) =√11, ну и осталось подставить и найти угол бета через дерадианную дробь второго типа: β≡ [√11& 3]…

Ответ: α≡ [5& 3], β≡ [√11& 3].

Задача 4

Перевести углы альфа и бета из предыдущей задачи 1 в обычные углы в градусах.

α≡ [5& 3] ≡ [5/3] =2arcSin [5/ (2*3)] = (1.97022…) r=112.885…°

β≡ [√11& 3] ≡ [√11/3] =2arcSin [√11/ (2*3)] = (1.17137…) r=67.1146..°

Ответ:

α≡ 112.885…°, β≡67.1146…°

2.8. Сравнение дерадианных дробей

Так как множество дерадианных дробей непрерывно и строго упорядочено в связи с тем, что дроби отображают углы, а углы на окружности (числовой окружности) располагаются непрерывно (так как каждому углу можно сопоставить точку на окружности, а линия окружности, как мы знаем, в каждой точке своей непрерывна), поэтому их можно сравнивать. Интересный возникает сразу вопрос: как можно сравнивать две де-дроби между собой? Ну для начала их надо привести к одному и тому же знаменателю, и та дерадианная дробь считается и есть большая, у которой числитель больше. В общем, все как и у обычных дробей. Запишем это через определение.

Определение 2.8.1

Две дерадианные дроби можно сравнивать, только если у них одинаковые либо числители, либо знаменатели, и та дробь считается большей, у которой больше числитель (знаменатель). И вообще дерадианные дроби сравниваются по правилам сравнения обыкновенных дробей.

Это значит, что дерадианные дроби можно сравнивать как обычные дроби по правилу сравнения обычных дробей, представить числитель и знаменатель их отношением в виде обычной дроби и сравнивать по числителю, при равных знаменателях, это очень бывает удобно и полезно при решении задач. Вообще дерадианные дроби можно упорядочивать двумя способами, первый: это как обычные дроби, а второй — на окружности, как углы. Давайте рассмотрим первый случай на примере дерадианной дроби первого типа,

Пример 1:

Сравнить две дерадианные дроби: (1& 1) и (3& 2).

Ну, во-первых, приведем их к одному общему знаменателю, для этого мы любую из дробей умножим пропорционально на одно и то же число и сравним числители. Давайте вторую дробь приведем к нормальному приведенному виду:

(3& 2) = (3*1/2& 2*1/2) = (3/2& 1) = (1.5& 1),

Так как 1 <1.5, это значит, что дерадианная дробь:

(1& 1) <(3& 2)

И действительно, первой дерадианной дроби соответствует примерно угол 53.1301°, а второй — 73.7398°. Это правило касается только первых двух типов, для третьего типа это правило сравнения не работает, поэтому давайте запишем это правило сравнения дробей первого и второго типа в общем виде, см. рис. 2.8.1.

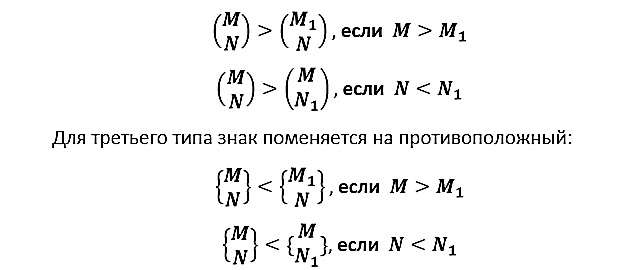
Пример 2:

Сравнить две дерадианные дроби:

{14& 45} и {28& 57}

Давайте приведем их к общему числителю 28: {28& 90} и {28& 57}, для третьего типа дроби та дробь будет больше, у которой знаменатель больше, 90> 57, откуда следует, что дробь:

{28& 90}> {28& 57} или {14& 45}> {28& 57}, и действительно, первой дерадианной дроби соответствует примерно угол 143.7476°, а второй — 121.1573°.

Глава 3. Образующие прямоугольные треугольники

3.1. Взаимно однозначное соответствие между пифагоровым прямоугольником и дерадианным треугольником для дерадианных углов всех трех типов

В предыдущей главе мы рассмотрели какие-то начальные понятия типа «дерадианный угол» или «дерадианная дробь», «дерадианный треугольник» и так далее. А в этой главе перейдем к изучению взаимодействия между прямоугольными треугольниками и дерадианными углами всех трех типов (связи будут все разные) и так же поймем их глубокую общую взаимосвязь.

Так как дерадианная дробь — это все-таки угол и отражает понятие угла в большей степени, то хотелось бы в первую очередь изучить эту связь. Ну что, не будем затягивать, скорей приступим!

Лемма 1

Для каждого дерадианного треугольника с углом α n-го типа всегда найдется или поставится во взаимно однозначное соответствие свой прямоугольный треугольник с углом α, и причем только один до порядка подобия.

Доказательство

Ну это и понятно, в принципе, если у прямоугольного треугольника всего три угла, из которых один прямой, второй α, то третьему углу ничего не остается, как быть величины π/2-α, а это и значит, что нашему углу α дерадианного треугольника ставится однозначно в соответствие тройка углов {π/2, α, π/2-α}, что и требовалось доказать.

Это лемму можно доказать также и геометрически, например, если вписать наш дерадианный треугольник в окружность, то в эту окружность также всегда можно вписать и единственным образом (до порядка симметрии и пропорциональности) прямоугольный треугольник, опирающийся катетом на апофему, и с углом в вершине, равной углу вершины дерадианного треугольника, а гипотенузой, равной двум радиусам 2r, описанной окружности вокруг дерадианного треугольника, то есть гипотенуза будет диаметром этой окружности, так как прямой угол будет лежать на окружности.

См. рис. 3.1.1.

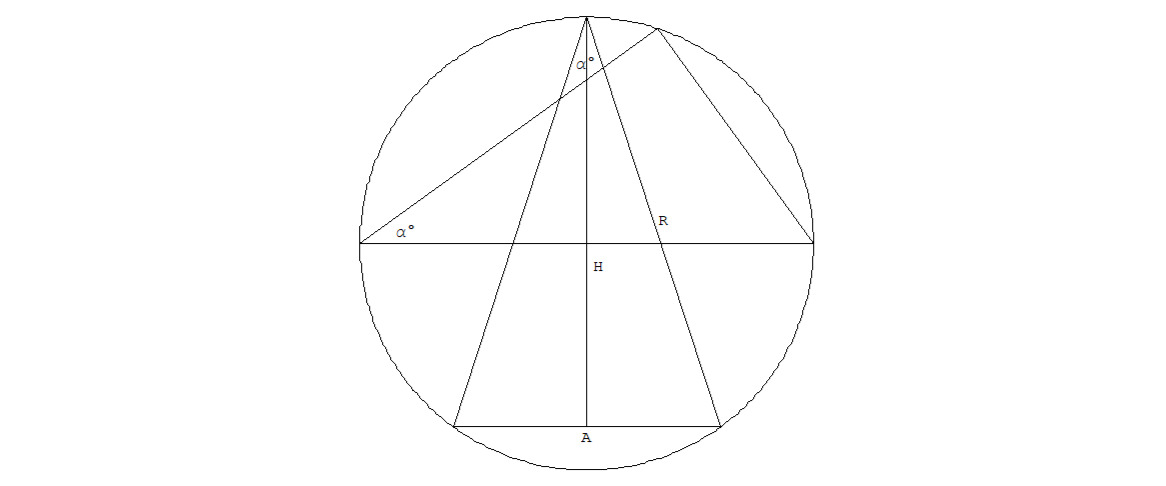
И из рисунка видно, что каждому описанному дерадианному треугольнику будет соответствовать только один прямоугольный треугольник (до порядка симметрии и пропорциональности линейных размеров). Что и требовалось доказать.

Дальше разберем все три типа дерадианных дробей по порядку и найдем, каким же их дерадианным треугольникам соответствуют их прямоугольники.

Теорема 3.1.1

(первый случай — множество {A, H})

Каждому дерадианному треугольнику с дерадианной углом первого типа при вершине: α ≡ (A& H), где

{A, H} — какие-то целые натуральные или просто вещественные числа, то будет всегда взаимно-однозначно соответствовать пифагоров прямоугольный треугольник со сторонами:

{4H2-A2, 4AH, 4H2+A2} = {R┴2,4AH, R2},

где, {4H2-A2, 4AH} = {R┴2,4AH} катеты,

и {4H2+A2} = R2 — гипотенуза

и обратная теорема:

Теорема 3.1.2

Каждому пифагоровому треугольнику со сторонами

{m2-n2, 2mn, m2+n2} всегда однозначно найдется дерадианный треугольник с дерад. углом при вершине первого типа с целыми натуральными {A, H}, такими, что A=n, H=m/2.

Доказательство

Сопоставим между собой два треугольника, дерадианный и пифагоров, см. рис. 3.1.2.

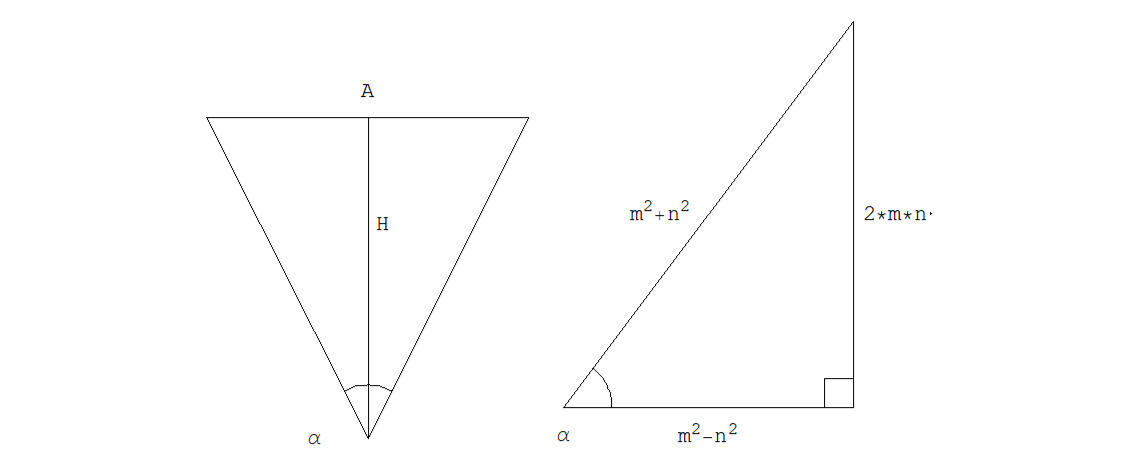
Мы знаем, что для любого дерадианного треугольника угол при вершине выражается формулой 2.4.1 (обратная формула перехода, или формула скалярный вид угла, см. параграф 2.4), а именно:

…… … … … … … …α= (A/H) =2ArcTan [A/ (2*H)]

Запишем эту формулу по-другому, упростив по формуле удвоенного арктангенса,

…… …α=ArcTan [(2*A/2H) / (1- (A/2H) 2)] =

….=ArcTan [(A/H) / ((((2H) 2-A2) / (2H) 2))] =

…… … … … … …=ArcTan [4AH/ ((2H) 2-A2)]

Также мы знаем, если нам дан пифагоров прямоугольный треугольник со сторонами:

…… … … {m2-n2, 2mn, m2+n2},

…… … …где (m, n) =1, и {m, n} — разной четности,

то для него уже угол α будет равняться через арктангенс противолежащего катета к прилежащему, см. рис. 3.1.2:

…… … … … … … … … α=ArcTan [2mn/ (m2-n2)]

И так как по лемме 1 мы ставим дерадианный треугольник в соответствие с пифагоровым и их углы α равны, то, приравняв и сопоставив эти формулы, так как они равны по равному углу, найдем полное соответствие между пифагоровым прямоугольным треугольником и дерадианным.

…… … … … … … …ArcTan [2mn/ (m2-n2)] =

…… … … … ……..=ArcTan [4AH/ (4H2-A2)]

…… … ….. …..2mn/ (m2-n2) =2AH/ (4H 2-A2)

Откуда приравняем числитель к числителю, а знаменатель — к знаменателю, так вот эти две дроби несократимые, это следует из определения пифагорова треугольника об элементарных решениях. И дерадианный треугольник мы также рассматриваем как несократимый. Поэтому мы можем числители и знаменатели этих дробей приравнять друг к другу. И, решив систему из двух уравнений, придем к следующему:

……m*n=2AH, m2-n2= 4H2-A2→ {n=A, m=2H}

Далее, подставив в формулу 3.1.1 вместо m и n апофему и высоту, получим стороны пифагорова треугольника, выраженного через апофему и высоту дерадианного треугольника.

Тогда окончательно получим:

…{4H2-A2, 4AH, 4H2+A2} = {R┴2,4AH, R2}, где

…{4H2-A2, 4AH} = {R┴2, 4AH} — катеты, а

…{4H2+A2} = {R2} — гипотенуза.

Что и требовалось доказать.

Для наглядности изобразим это на рисунке.

См. рис. 3.1.4.