
Бесплатный фрагмент - Основы R-анализа
Аннотация. Монография «Основы R-анализа» посвящена введению в новое математическое направление — релятивистский анализ количества, согласно которому идея количества является относительной и однозначно определяется только в рамках так называемых количественных систем, в том числе относительными являются понятия конечного и бесконечного — конечное в одной количественной системе может оказаться бесконечным в другой и наоборот. На этой основе принципиально расширяется понятие числа, и наряду с господствующим сегодня «фаустовским числом» вводится представление о «пифагорейском числе», лежащем в основе жизни и сознания. Даются основания нового математического аппарата, позволяющего работать с бесконечными величинами как с конечными. Приводятся многочисленные примеры применения R-анализа к различным прикладным задачам.
Монография будет полезна всем тем, кто интересуется новыми направлениями математики и логики, философии математики и интегрального подхода.
Рецензенты
Буданов Владимир Григорьевич, руководитель сектора междисциплинарных проблем научно-технического развития Института философии РАН, кандидат физико-математических наук, доктор философских наук, главный научный сотрудник ИФРАН
Троицкий Виктор Петрович, старший научный сотрудник «Дома А. Ф. Лосева»
Введение
В современной математике создан специальный математический аппарат, который наиболее адекватно на данный момент выражает идею количества. Это аппарат математического анализа, в основе которого лежат методы дифференцирования и интегрирования. Центральное понятие здесь — понятие предела. Берётся последовательность чисел, которая всё более сгущается вокруг некоторого числа. Последнее и называется пределом этой последовательности.
Теория пределов стала обоснованием линии Ньютона в построении исчисления бесконечно малых. Кроме Ньютона, была ещё линия Лейбница. Они по-разному понимали, что такое бесконечно малая величина. Лейбниц представлял её как актуальную величину, которая лежит между всеми ненулевыми числами и нулём. Но такая позиция в то время вызывала трудности. Победила линия Ньютона, который предлагал рассматривать бесконечно малую как потенциальную величину — процесс бесконечного приближения к нулю. Подобную программу удалось обосновать к 19 веку, и она стала господствующей в современной математике, пока в веке 20-м Абрахаму Робинсону не удалось всё же строго обосновать лейбницевское понимание бесконечно малой как актуальной величины в рамках так называемого «нестандартного анализа».
В настоящей работе будет представлен эскиз нового математического аппарата, который развивает идеи математического анализа на новом уровне, не отвергая, а дополняя этот аппарат новыми конструкциями. Название нового аппарата — R-анализ, что сокращает более развёрнутое название «релятивистский анализ количества». Релятивистский — значит относительный. Важный эффект, возникающий в R-анализе, — установление относительности тех или иных количественных определений, в первую очередь состояний конечного и бесконечного. Подобно тому как в механике многие определения зависят от системы отсчёта, в которой представлено движение, подобно этому в R-анализе возникают как бы свои системы отсчёта («количественные системы»), в рамках которых количество может получать то или иное своё определение. Конечное в одной количественной системе может оказаться бесконечным в другой и наоборот.
Мы предполагаем знакомство читателя с основными понятиями стандартного математического анализа, как он преподаётся на первом и втором курсах математических или физических факультетов. Опираясь на его определения, будет дан проект обогащения этого подхода идеями и структурами R-анализа.
Но вначале несколько философских рассуждений.
Глава 1. Индуктивное введение в R-анализ
1. Стандартная количественная система
В лице R-анализа будет предложена новая теория количества, в связи с чем закономерно возникает вопрос, что такое количество?
Под количеством мы будем понимать то, что можно измерить. Это может быть вес, длина, объём и т. д. Любое количество — это количество какого-то качества. Количество возникает, когда происходит изменение внутри качества, так что нечто меняется, а качество при таком изменении остаётся неизменным. Тогда и говорят о количестве. Например, вес тела может возрастать или уменьшаться, но при количественных преобразованиях веса само качество веса продолжает оставаться неизменным. Поэтому философы давно связали между собой категории количества и качества. Количество — это внутреннее изменение качества, когда качество продолжает сохраняться, и меняются только его степени. В таком виде количество вообще невозможно определить без качества. Они идут в паре.
Но количество может в своём изменении рано или поздно достигнуть границы качества, где данное качество исчезает и возникает иное качество. Например, если мы нагреваем воду всё больше и больше, то она наконец закипает и перестаёт быть жидкой водой, переходя в пар. В этом случае качество проецируется на количество в виде границ качества, в чём проявляется уже третья категория — мера качества.
Мера — это границы качества на количественной шкале. В категории меры происходит определённый синтез категорий количества и качества, что было отмечено ещё в философии Гегеля.
В своей границе качество встречается с количеством. Если при внутреннем изменении количество меняется, а качество остаётся неизменным, то при достижении границы качества происходит как изменение количества, так и качества.
Так в первом приближении взаимодействуют между собой категории количества, качества и меры, и в целом они образуют некоторую систему, которую так и можно называть — количественная система. Она включает в себя некоторое качество, внутреннее изменение которого даёт количество данного качества, а границы системы выражают границы данного качества на количественной шкале. Итак, можно использовать следующее определение.
Количественная система — такой вид единства количества и качества, когда есть изменение количества (внутреннее количество), сохраняющее данное качество, а также определены границы количества, при которых данное качество переходит в другое качество, что в целом, в единстве качества, внутреннего количества, количественных границ и качественных скачков на границе выражает идею меры как взаимопроникновения количества и качества.
Можно сказать и так, что количественная система — это проекция качества на количество, когда при такой проекции образуется та область количества со своими границами, внутри которой качество сохраняется, а при достижении границ этой области происходят качественные скачки и смены качеств. В общем случае могут быть разные границы, например, верхние и нижние границы в данной количественной области, и достижение разных границ выражается в смене данного качества разными смежными качествами.
Отсюда вытекает ряд сопутствующих определений.
Внутреннее количество — количество, изменение которого сохраняет одно и то же качество.
Внешнее количество — количество, изменение которого пересекает границу количественной системы и приводит к смене качества.
Смежные качества — качества, имеющие общую количественную границу между собой, переход которой приводит к исчезновению одного качества и возникновению другого.
Количественная система — это единство своего качества, внутреннего количества и своих границ.
Количественную систему можно определить таким образом как пару (Q,X), где Q — качество, [Х] — количество этой системы, взятое вместе со своим границами ∂X, т.е.
[X] = X ∪ ∂X,
где ∪ — операция объединения.
Здесь Х = Int [X] — внутренность [X], т.е. внутреннее количество данной количественной системы.
Внутреннее количество Х может быть как одномерным (подмножеством множества вещественных чисел), так и многомерным (подмножеством многомерного пространства).
Поищем с этой точки зрения количественные системы в математике.
Возьмём ряд натуральных чисел 1, 2, 3,… Можно ли его считать количественной системой?
Ответ на этот вопрос будет зависеть от того, какое качество мы рассматриваем.
Если мы возьмём качество «натуральности» («быть натуральным числом»), то да, в лице натурального ряда мы имеем дело с количественной системой, поскольку на протяжении всего ряда это качество остаётся неизменным, и обнаруживает оно свои границы при переходе к другим числам, например, отрицательным или дробным.
Но переход от натуральных к целым или рациональным числам не является слишком сильным, поскольку он не связан с бесконечностью. Одна вторая ½ всё же конечно отличается от единицы 1, как и минус единица -1. А вот если мы имеем дело с вещественными числами, то их границы уже уходят до бесконечности — бесконечно малого или бесконечно большого. И выход за границы качества здесь уже связан с достижением бесконечности, т.е. выступает как особенно сильная трансформация.
Количественные системы, где как верхняя, так и нижняя границы количества уходят на бесконечность, можно называть сильными количественными системами. Множество вещественных чисел — это минимальная сильная количественная система.
Почему не рациональные числа?
Дело в том, что рациональные числа представляют собой только внутреннее количество того же качества, что представлено и в вещественных числах. Внутреннее количество — количество качества, не достигающее границ этого качества. И тогда такое количество не может представлять всю количественную систему, в которую входит и количество, и качество, и границы этого количества.
Переход от рациональных к вещественным числам, как известно, связан с пополнением рациональных чисел иррациональными, а последние могут быть выражены только бесконечными нестационарными последовательностями рациональных чисел, что выражает граничное количество количественной системы.
В самом деле, любое иррациональное число несоизмеримо с единицей для любой сколь угодно малой, но конечной доли единицы. И только на уровне бесконечно малой доли единицы иррациональное число достигает предельной соизмеримости с единицей. Отсюда же органично возникает и тема бесконечно малого.
Можно сказать и так, что иррациональные числа предполагают как бы разбиение единицы на бесконечно малые доли, бесконечно большими суммами которых они только и могут быть выражены.
Например, число π = 3.14159… невозможно полностью выразить конечной десятичной дробью, но только бесконечной. Поскольку любая положительная десятичная дробь α — это сумма какого-то числа единиц n плюс сумма сумм всё меньших долей единицы
α = n + m110—1 + m210—2 + m310—3 + …, где mi ∈ {0,1,…,9}, i =
= 1,2,…,
и для иррационального числа этот ряд бесконечен, то это и значит, что такое число можно выразить только на уровне сумм бесконечно малых долей единицы. В самом деле, более крупные доли единицы можно выразить в свою очередь как суммы меньших долей, так что в конечном итоге всё число можно выразить как сумму наименьших долей единицы.
Например, если
α = n + m110—1 + m210—2,
то n = n10210—2, m110—1 = m110110—2,
так что в итоге получим:
α=n10210—2+m110110—2+m210—2 = (n102+m1101+m2) 10—2,
т.е. представление числа как суммы целого числа наименьших долей единицы, присутствующих в структуре этого числа.
Таким образом, только на уровне вещественных чисел (объединения рациональных и иррациональных чисел) мы впервые имеем дело с сильной количественной системой, которая содержит в себе свои границы, и достижение этих границ связано с бесконечностью.
Стандартный математический анализ делает предметом своего основного исследования эту количественную систему, явным образом дополняя границы иррациональных чисел бесконечно малыми элементами.
Количественная система вещественных чисел отлична от предыдущих систем тем, что она сильная, т.е. переход к её пределам требует бесконечности, в отличие от предыдущих систем. Поэтому эта система особенно сильно проявляет своё качество и полагает сильную границу ему. Вот почему работа именно с этой системой оказалась такой плодотворной и позволила создать гораздо более глубокий математический аппарат, работающий не просто с количеством, но со всей системой «количество — качество — мера».
Проблема только оказалась в том, что математика остановилась на этом рубеже и не идёт дальше, развивая диалектику количества и качества. R-анализ как раз и пытается это сделать, предлагая работать по-настоящему с мерной математикой.
2. Количественные системы конечного и бесконечного количества
Как же дальше можно развивать диалектику количества и качества?
Самое интересное состоит в том, чтобы заглянуть за границы некоторого бесконечного качества. Если есть сильная количественная система с бесконечными верхним и нижним порогами, то можно попытаться не только достичь её границ, но и выйти за эти границы.
Что там — за границами качества?
Отчасти уже стандартный математический анализ отвечает на этот вопрос. Например, он говорит, что за нижней границей конечного количества находится бесконечно малое количество. Есть определённая алгебра бесконечно малых. Например, их можно складывать и умножать, можно одну бесконечно малую поделить на другую. В этих операциях нужно быть осторожными. И аппарат пределов позволяет более строго работать с этой алгеброй бесконечно малых.
Например, у нас есть две бесконечно малые β1 и β2 как бесконечные последовательности вещественных чисел
β 1 = {r1n} ∞n=1,
β 2 = {r2n} ∞n=1,
которые имеют пределом ноль:
limn→∞r1n = 0,
limn→∞r2n = 0.
Тогда операции на них можно задать как покоординатные операции на последовательностях, например:
β1 + β2 = {r1n} ∞n=1 + {r2n} ∞n=1 = {r1n +r2n} ∞n=1.
Осторожность в этом случае нужно соблюдать, поскольку такие операции не всегда являются внутренними для бесконечно малых, т.е. они могут вывести за область бесконечно малых величин, например, при делении одной бесконечно малой на другую.
Если же мы умножаем одну бесконечно малую на другую, то возникает бесконечно малая более высокого порядка, т.е. бесконечно малые образуют множества разных порядков.
Причём, каждое множество бесконечно малых одного порядка изоморфно множеству вещественных чисел. В самом деле, если у нас есть некая бесконечно малая β, то 1) все величины rβ, где r — вещественное число, также будут бесконечно малыми, и 2) это будут бесконечно малые того же порядка, что β. Тем самым мы устанавливаем изоморфизм между множеством вещественных чисел r и множеством бесконечно малых вида rβ. На таких бесконечно малых можно определить внутренние операции, которые не будут выводить за это множество, по правилу:
r1β o r2β = (r1 o r2) β,
где о — некоторая операция на вещественных чисел.
Ту же самую методологию можно распространить и на бесконечно большие величины, если так же понимать их как предельные последовательности, имеющие своим пределом бесконечность ∞.
Таким образом, если множество вещественных чисел представляет собой сильную количественную систему, то любое множество бесконечно малых или бесконечно больших вида rβ также будет представлять собой сильную количественную систему, изоморфную множеству вещественных чисел по своей внутренней структуре.
В итоге стандартный математический анализ начинает работать не только с вещественными числами, но и с бесконечными величинами (бесконечно малыми и бесконечно большими), т.е. он выступает как первая техника работы с разными сильными количественными системами.
Отсюда мы можем дать первый ответ на поставленный выше вопрос: что там за границами качества?
За границами качества конечного количества находятся качества бесконечных количеств — бесконечно малых и бесконечно больших. Возможна математика работы с количествами этих качеств. Математический анализ и представляет такую математику. В этом его сила.
Во многом то же самое делает и нестандартный анализ Абрахама Робинсона, только бесконечные он начинает понимать актуально. Что же касается алгебры, то в нестандартном анализе доказывается так называемый принцип переноса, который позволяет установить высокое соответствие между вычислениями стандартного и нестандартного математического анализа.
Ну вот, казалось бы, всё хорошо. У нас есть математика не только одной сильной количественной системы, но и множества их, и именно те новые эффекты, которые связаны с отношениями этих систем и переходами между ними, и составили самые ценные аспекты математического анализа как более глубокой и диалектической теории количества.
Но оказывается не всё так хорошо, как видится на первый взгляд. Разовьём эту тему более подробно.
3. К новому пониманию актуальной бесконечности
Проблема связана с пониманием бесконечности.
Сегодня есть две основные концепции бесконечности — как потенциальной и актуальной. Потенциальная бесконечность недостижима — сколько бы мы не стремились к её границе, мы никогда не сможем её достичь. Такова, например, бесконечность ∞ как предел натурального ряда 1, 2, 3, …. Что же касается актуальной бесконечности, то она рассматривается как количество, достигшее своего рубежа. Но если это так, то, следовательно, появляется достижимость бесконечности, достижимость того конца количественного процесса, который в потенциальной бесконечности был недостижим. Но какая же это без-конечность, если появляется конец, если конец оказывается достижим? Следовательно, идеей актуальной бесконечности предполагается момент достижимости конца количественного процесса, т.е. отрицание его бесконечности, т.е. конечность этого процесса.
Вот этот момент недооценивается или вовсе не понимается в современной математике.
Не понимают, что актуальная бесконечность есть всегда уже некоторая конечность, которая совмещается с бесконечностью. В актуальной бесконечности есть как бы два плана её определения: 1) внутренний план потенциальной бесконечности, согласно которому предел количества по прежнему недостижим, 2) внешний план конечности, в рамках которого бесконечный рубеж достигается и становится конечным. И актуальная бесконечность есть некая координация этих двух планов.
Но не отрицают ли друг друга эти два плана? Возможно ли их совмещение? Не является ли в связи с этим понятие актуальной бесконечности внутренне противоречивым?
Нет, не является. И это можно проиллюстрировать простым примером. Рассмотрим не просто натуральный ряд 1, 2, 3,…, а его образ вида f (1), f (2), f (3),…, где f — такая функция, что ряд f (n) имеет конечный предел при n→∞. Причём, пусть и метрические определения между рядами n и f (n) будут изоморфными, т.е. n1 <n2 влечёт f (n1) <f (n2). Например, f (n) = arctg (n).
В этом случае мы видим два плана в последовательности f (n), и эти планы непротиворечиво координируются между собой. План потенциальной бесконечности остался в последовательности f (n), в силу её изоморфизма последовательности натурального ряда n. И в рамках этого изоморфизма, предел f (∞) так же не достижим для любого элемента f (n), как бесконечность ∞ не достижима для любого конечного элемента n. Но появляется и второй план — план конечного отношения между пределом f (∞) и элементами f (n), поскольку f (∞) есть конечное число.
Такую двойственность отношений можно выразить выделением не просто двух планов, но двух видов метрических отношений (метрик), связанных с этими планами.
Напомним, что в общем случае метрика ρ (х,у) для элементов х, у из линейного пространства П есть такая вещественная функция, которая подчиняется следующим основным условиям:
1) тождество: ρ (х,у) = 0 е.т.е. х=у,
2) позитивность: ρ (х,у) ≥0,
3) симметричность: ρ (х,у) = ρ (у,х),
4) неравенство треугольника: ρ (х,z) ≤ρ (х,у) + ρ (y,z).
На элементах f (n) можно ввести внутреннюю метрику:
ρn (f (n1),f (n2)) = |n1 — n2|,
и внешнюю метрику
ρex (f (n1),f (n2)) = |f (n1) — f (n2) |,
где |x| — модуль вещественного числа х.
По внутренней метрике элемент f (∞) недостижим (несоизмерим), т.е расстояние до него от любого элемента f (n) бесконечно:
ρin (f (n),f (∞)) = |n — ∞| = ∞,
а по внешней метрике он вполне достижим и соизмерим с элементами f (n), т.е. расстояние до него конечно:
ρex (f (n), f (∞)) = |f (n) — f (∞) | <∞.
И обе метрики согласованы между собой в рамках изоморфизма f.
Таким образом, на этом примере мы видим, что могут быть не просто два плана определения бесконечности, но и связанные с ними метрические определения, задающие предел количественного процесса как одновременно и достижимый, и недостижимый для элементов внутреннего количества.
Именно такую конструкцию двух планов и двух метрик и следует, с нашей точки зрения, всегда предполагать, когда речь заходит об актуальной бесконечности.
Когда строится математический анализ, оперирующий с бесконечными как достижимыми состояниями другой количественной системы, то здесь мы имеем концепт актуальной бесконечности, и, следовательно, должны быть два плана её определения и две связанных с ними метрики. Но наличие внешней метрики, как можно было видеть выше, делает бесконечные элементы конечными. В то же время как в стандартном, так и нестандартном анализе все бесконечные элементы (бесконечно малые или большие) остаются только бесконечными. Такая же ситуация существует и в теории множеств, где бесконечные множества мыслятся актуальными и остаются только бесконечными.
С нашей точки зрения, используемый до сих пор концепт актуальной бесконечности, где отсутствует конечная внешняя метрика для бесконечных элементов, представляет некоторый крайний случай построения концепта актуальной бесконечности, при котором внешний план используется с ограничением по внешней метрике. Это значит, что внешний план позволяет оперировать с бесконечными элементами наряду с конечными, но метрически такое соизмерение ограничено только рамками некоторых условных определений. Соизмеримость захватывает ограниченный операциональный аспект множества количественных систем.
Да, по-видимому, такой крайний случай определения актуальной бесконечности так же возможен, но он представляет собой некоторое крайнее состояние, которое не является основным в понимании феномена актуально бесконечного. В рамках R-анализа предполагается понимание актуальной бесконечности в координации как двух операциональных планов, так и двух систем метрических определений различных количественных систем. В частности, это означает в том числе конечность бесконечных элементов в рамках определений внешней метрики.
Когда мы переходим к внешней позиции, где соизмеряются конечное и бесконечное, и они оказываются двумя конечностями, то мы попадаем в новую количественную систему с более глобальным качеством, для которого выход за границы прежнего качества будет продолжать оставаться внутренним изменением. Поэтому позиция соизмерения конечного и бесконечного обязательно должна предполагать момент количественного отношения — внутреннего отношения для более глобального качества, соизмеряющего качества конечного и бесконечного. Такое более глобальное качество можно было бы называть конечно-бесконечным или фин-инфинитным, ещё короче: ф-инфинитным.
Теперь вопрос в том, как более строго и непротиворечиво можно было бы строить такого рода математику финфинитного?
4. R-функции как границы количественных систем
Выше мы видели, что важную роль в координации двух позиций и метрик актуально бесконечного играет некоторая функция f, которая в нашем примере сжимала натуральный ряд чисел в предельную последовательность с конечным пределом. Благодаря такому сжатию, определялась внешне-метрическая позиция актуально бесконечного. Эту идею можно обобщить, распространяя её с натурального ряда на всё множество вещественных чисел и предполагая некоторую функцию R-1М, которая изоморфно сжимает множество вещественных чисел R в интервал (-М,М), где М> 0, — подмножество R. В этом случае финитизируются две бесконечности +∞ и -∞, где R-1М (∞) = М и R-1М (-∞) = -М. Такую функцию я буду называть обратной базовой R-функцией. К ней нужно предъявить ряд требований.
Все эти требования в конечном итоге вытекают из общей идеи, что функция у = R-1М (х) должна быть аналогом функции у = х при представлении бесконечности ∞ в виде конечного числа М. Более строго это можно выразить в виде условия:
limM→∞R-1M (x) = x,
т.е. обратная R-функция с верхним порогом М должна переходить в тождественное отображение у = х при стремлении М к бесконечности.
Чтобы определить свойства функции R-1М, нужно взять отображение у = х и трансформировать его до у = R-1М (х), изоморфно сжимая вещественную числовую ось в интервал (-М,М). Такова интуиция. Из неё можно вывести следующие основные свойства.
Во-первых, как уже было отмечено, функция у = R-1М (х) должна быть изоморфизмом, т.е. сохранять порядковые соотношения: х1 <х2 влечёт R-1М (х1) <R-1М (х2), и обеспечивать взаимно однозначное отображение между областью определения и значения.
Во-вторых, как и у=х, функция у = R-1М (х) должна быть непрерывной.
В-третьих, как и у=х, функция у = R-1М (х) должна быть нечётной, т. е. R-1М (-х) = -R-1М (х). Отсюда сразу же вытекает, что R-1М (0) = 0.
Этого пока достаточно. В ряде случаев можно потребовать, чтобы выполнялось свойство R-1М (1) = 1, а также функция у = R-1М (х) была дифференцируемой и dR-1M (0) /dx = 1.
Понятно, что раз функция у = R-1М (х) взаимно однозначна, то определена обратная к ней функция, которую будем обозначать как у = R+1М (х) и называть прямой базовой R-функцией. Она, наоборот, изоморфно разжимает интервал (-М,М) в бесконечную вещественную числовую прямую R.
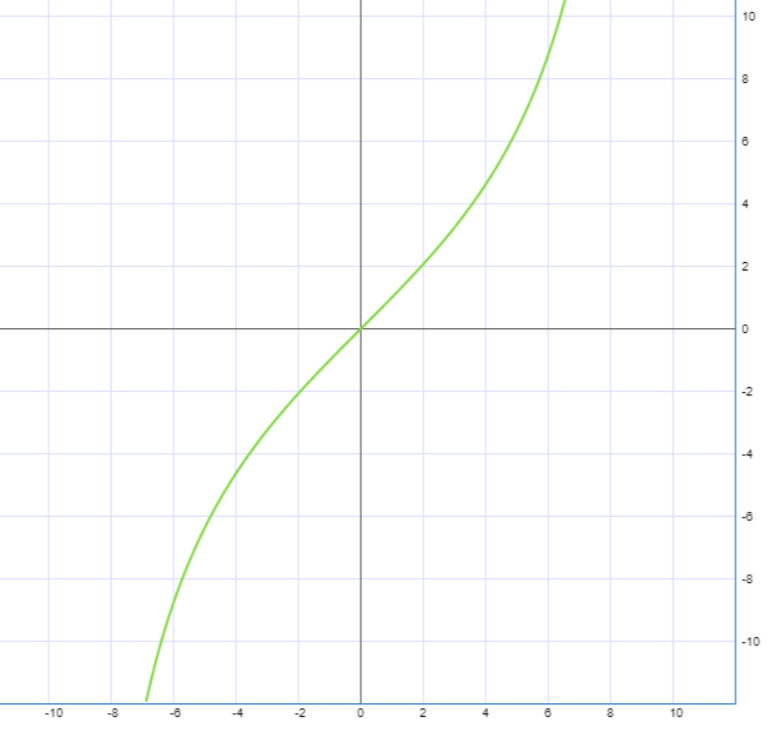
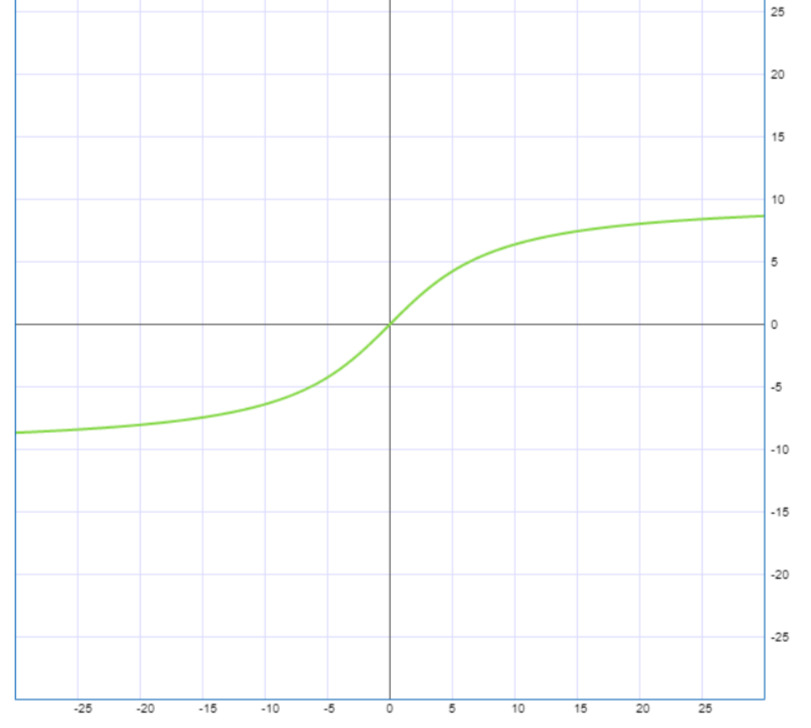
В качестве примера можно привести R-функции, построенные на основе функций тангенса и арктангенса:
R+1М (х) = (2M/π) tg (πx/2M),
R-1М (х) = (2M/π) arctg (πx/2M).
Графики этих функций для М=10 приведены на рис. 1 и 2.
Эти R-функции непрерывны и дифференцируемы. Для них выполняется условие limM→∞R-1M (x) = x. Например, учитывая, что ряд Маклорена для арктангенса имеет вид
arctg (x) = x — x3/3 + …,
для обратной R-функции получим:
(2M/π) arctg (πx/2M) = (2M/π) ((πx/2M) — (πx/2M) 3) /3+…) →
→ (2M/π) (πx/2M) = x при М→∞.
Хотя в общем случае свойство dR-1M (0) /dx = 1 не выполнено, но оно выполняется всё лучше при М→∞:
((2M/π) arctg (πx/2M)) ’ = (2M/π) (1/ (1+ (πx/2M) 2)) (π/2M) =
= (1/ (1+ (πx/2M) 2)) →1 при М→∞.
В нуле эти функции дают ноль, а вот в единице они не всегда дают единицу, но чем больше М, тем ближе значение R-1М (1) к единице.
В общем случае различных частных видов R-функций существует бесконечное множество. Пока мы ограничиваемся самыми общими к ним требованиями.
Используя R-функции, мы теперь более адекватно можем определить структуру актуальной бесконечности для вещественных чисел. Сделаем это на примере бесконечно большого.
Качество конечного охватывает всё множество вещественных чисел, и любое изменение внутри этого множества есть внутреннее изменение этого качества, т.е. его количество. В наибольшей степени количество качества конечного выражается рациональными числами, которые никогда не достигают границ конечного количества.
В случае иррациональных и вещественных чисел мы уже операционально достигаем границ конечного количества и даже переходим за эти границы в область бесконечного — бесконечно большого и бесконечно малого. Но пока это за-конечное количество дано неметрически — без внешней метрики, которая должна была бы конечно соизмерять конечное и бесконечное.
Как в стандартном, так и в нестандартном анализе бесконечное всегда остаётся бесконечным и никогда не может быть представлено конечным числом. Поэтому соизмерение конечного и бесконечного в этом случае лишь операциональное (участие в общих операциях), но не метрическое — так построена на сегодня любая версия математического анализа, как по Ньютону, так и по Лейбницу. В итоге подлинного обеспечения состояния актуальной бесконечности в этом случае достичь не удаётся. Чтобы это сделать, нужно добавить к внешней позиции бесконечности метрическое представление, которое сделает бесконечное конечным. Проиллюстрируем такой приём с помощью обратной базовой R-функции.
Мы сжимаем множество вещественных чисел в конечный интервал (-М,М) обратной базовой R-функцией, и бесконечности +∞ и -∞ теперь финитизируются и представляются числами М и -М соответственно. Кроме внутренней позиции конечного количества, теперь у нас появляется и внешняя позиция, в которой бесконечное оказывается актуальным, т.е. достижимым и даже переходимым далее, т.е. конечной величиной. Это и есть настоящая актуальность — данность как достижимого и переходимого далее состояния. Таким образом, сделать бесконечное актуальным означает в данном случае представить его как конечную величину во внешней позиции, благодаря обратной базовой R-функции.
Уточним ряд понятий.
Дана обратная базовая R-функция у = R-1М (х), которая отображает множество вещественных чисел R в интервал (-М, М), т. е. R-1М: R→ (-М,М). Интервал (-М,М) является подмножеством также множества вещественных чисел, но если быть точным, то здесь следует различать два множества вещественных чисел: 1) прообразное множество вещественных чисел, обозначим его R (0), которое является областью определения обратной базовой R-функции, и 2) образное множество вещественных чисел R (1), которое включает в себя как свою часть интервал (-М,М).
Такое разделение связано с тем, что у этих множеств два разных качества: если прообразное множество вещественных чисел R (0) представляет качество конечного количества, то образное множество R (1) — качество количества, которое соединяет в себе конечное и бесконечное для первого качества (R (1) выражает качество финфинитного количества).
Величина R-1М (∞) представляет собой настоящую актуальную бесконечность, определённую не только во внешней позиции, но и во внешней метрике. Заменяя представленную выше абстрактную функцию f на R-1М, получим для внутренней и внешней метрики следующие определения:
ρin (R-1М (х), R-1М (у)) = |х — у|,
ρex (R-1М (х), R-1М (у)) = |R-1М (х) — R-1М (у) |.
По внутренней метрике элемент R-1М (∞) является недостижимым для любого конечного элемента R-1М (х), т.е. расстояние между ними бесконечное:
ρin (R-1М (х), R-1М (∞)) = |х — ∞| = ∞,
а во внешней метрике элемент R-1М (∞) оказывается конечно достижимым (актуальным) для любого элемента R-1М (х), где х — вещественное число:
ρex (R-1М (х), R-1М (∞)) = |R-1М (х) — R-1М (∞) | = |R-1М (х) — M| <∞.
Так более полно может быть определена актуальная бесконечность («конечная бесконечность»), и в её определении, как видим, важную роль играет R-функция.
5. К новой модели бесконечно большого количества
В итоге мы начинаем постепенно входить в работу с аппаратом R-анализа. В основе этого аппарата, как видим, лежат R-функции.
В силу изоморфизма, обратная базовая R-функция R-1М позволяет полностью воспроизвести всю структуру вещественных чисел и связанных с нею дополнительных конструкций на интервале (-М,М). Например, мы можем определить R-сложение ⊕ между элементами х* = R-1M (х) и у* = R-1М (у) по правилу:
х*⊕у* = R-1М (R+1М (х*) + R+1М (у*)) = R-1М (х + у) = (х + у) *.
Аналогично поступаем и для всех остальных операций и предикатов.
Казалось бы, R-изоморфизм не даёт ничего нового уже по определению. Но, как было представлено выше, кроме изоморфных отношений, появляется также момент внешней метрики, который выходит за границы изоморфизма и позволяет оперировать с бесконечно большим количеством как с конечным числом.
Это означает, что за границами R-изоморфизма начинает проступать какая-то более богатая структура, которая хотя и скоординирована с R-изоморфизмом, но более или менее может выходить за его границы. Задача R-анализа теперь состоит в том, что всё более проявлять и оформлять такую структуру.
Попробуем сделать первый шаг в оформлении такой R-структуры на примере бесконечно большого как актуальной величины.
Когда мы сжимаем прообразное множество вещественных чисел R (0) обратной базовой R-функцией R-1М в интервал (-М,М) на образном множестве вещественных чисел R (1), мы по сути начинаем иметь дело с двумя количественными системами Q (0) и Q (0,1). Первая из них представлена множеством R (0), вторая — множеством R (1). Разница их состоит хотя бы в том, что у них разные границы качества. Если у первой количественной системы Q (0) качеством является конечность, которая своей верхней границей имеет бесконечно большое ∞, то вторая количественная система Q (0,1) делает границу ∞ первой системы конечной, в виде числа R-1М (∞) = М, и обладает более глобальным качеством конечно-бесконечного (финфинитного) (см. рис. 3).
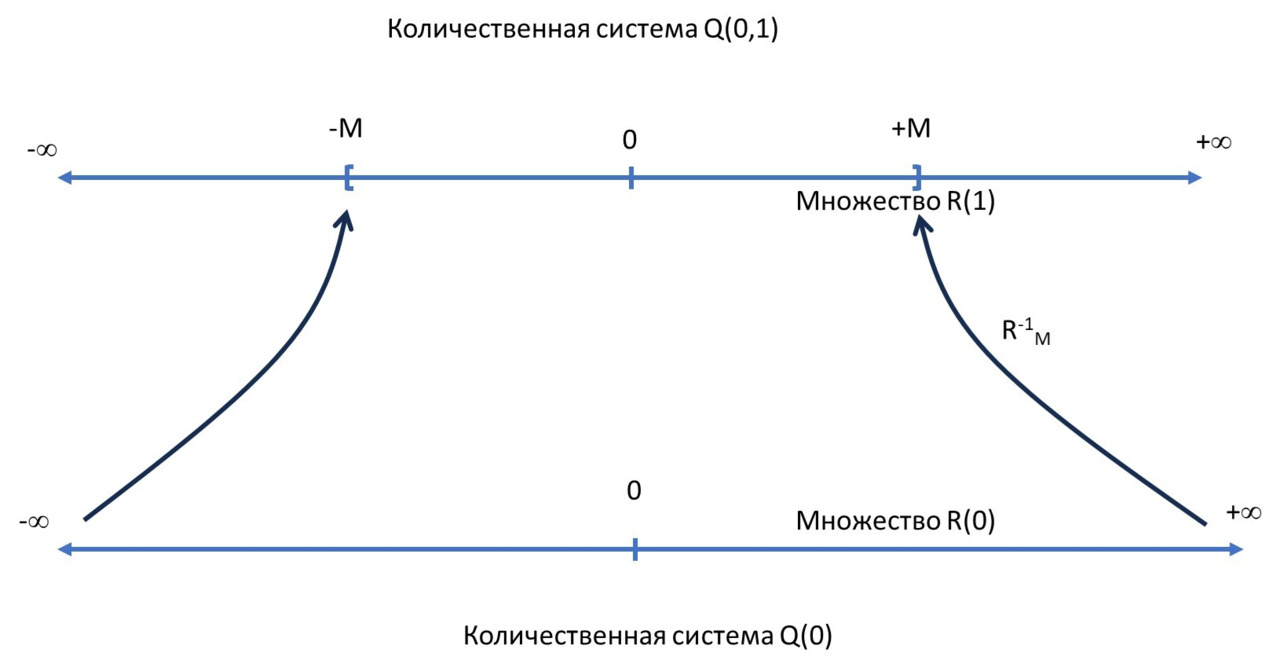
На рис. 3 вместо декартовской системы координат, где числовые оси аргумента и функции изображаются перпендикулярно друг другу, изображена другая система представления функции, где числовые оси аргумента и функции параллельны друг другу. Такая система имеет свои плюсы и минусы. Минус в том, что мы не видим график функции, но плюс состоит в том, что на плоскости можно изображать многократные функции от функций.
Строго говоря, вещественные числа х∈R (0) и х∈R (1), даже если это одно число х, следует различать между собой, поскольку это количества разных качеств. Это означает появление новой степени свободы при определении числа-количества — это параметр качества. Коль скоро мы вводим разные количественные системы, даже обладающие изоморфными количествами, то всё же эти количества теперь приходится различать, поскольку у них разные качества. Далее я буду называть новую степень свободы, связанную с качеством количественной системы, слоем или количественным слоем. По сути, слой — синоним качества количества.
Итак, количественные системы Q (0) и Q (0,1) обладают разными качествами-слоями, и параметр слоя открывает новые измерения и многообразия в организации количества, вводя качественные параметры в математику наряду с количественными.
Как более операционально выразить принадлежность одного и того же вещественного числа х к разным слоям?
Положим, что слой количества — это новое измерение в некотором многомерном пространстве. Тогда одно число х разных слоёв будет лежать как бы в разных измерениях, что можно выразить парами (х,0) — х одного слоя, (0,х) — х другого слоя.
Пусть, например, первая координата в паре (х,у) выражает элемент х из первой количественной системы Q (0), второй элемент у — из второй системы Q (0,1). Слой количества в этом случае будет выражен номером координаты в паре.
Хорошо, пусть будут пары. Но тогда должна возникнуть некоторая структура на этих парах. Что это за структура?
Вернёмся вновь к смыслу пар (х,у). Элемент х выражает количество системы Q (0), которая представлена множеством R (0), а элемент у — это элемент из множества R (1) системы Q (0,1). Внутри себя эти элементы полностью воспроизводят структуры вещественных чисел, т.е. для частного случая пар (х,0) и (0,у) можно просто задать структуру поля вещественных чисел и связанные с нею конструкции. Проблема возникает, когда мы имеем дело с двукоординатной парой (х,у), где х и у не равны нулю. Как работать с такими парами?
Здесь мы должны вспомнить об R-функции, которая сжимает множество R (0) в интервал (-М,М) на множестве R (1). Тем самым она делает элементы у≥М на множестве R (1) бесконечно большими для R (0). То есть множество R (1) — это область бесконечно большого количества для количества из R (0). По крайней мере, это верно для элементов у≥М из R (1).
А как быть с элементами у∈ (-М,М) из R (1)?
Эти элементы изоморфны элементам из множества R (0), которое выражает конечное количество. Следовательно, множество R (1) включает в себя как конечные элементы системы Q (0), так и бесконечные относительно неё элементы. Это и значит, что система Q (0,1) является конечно-бесконечным количеством относительно системы Q (0). Она финфинитна.
Только бесконечность системы Q (0,1) — это не бесконечно малое, а то бесконечно большое, которое выражает как плюс-, так и минус-бесконечность. Можно называть такое бесконечно большое модульным, обозначая его символом ±∞. На множестве R (1) модульному бесконечно большому будут соответствовать полуинтервалы (-∞, -М] и [M+∞). Количественную систему, определённую на этих полуинтервалах, обозначим через Q (1) — как систему модульного бесконечно большого количества.
Таким образом, качество системы Q (0,1) объединяет в себе конечное и модульное бесконечно большое, если представлять это качество со стороны системы Q (0).
Если в системе Q (0) между конечным и модульно бесконечно большим, как ±∞, определена бесконечная несоизмеримость, то в системе Q (0,1) эти состояния количества соизмеряются между собой как две конечности: интервал (-М,М) и объединение двух полуинтервалов (-∞, -М] ∪ [M+∞).
Если мы будем находиться в одной количественной системе, то получим свои виды конечного и бесконечного с бесконечной несоизмеримостью между ними. Только координация двух и более количественных систем позволяет ввести новые состояния количества — бесконечное как конечное (R-1М (∞)), конечно-бесконечное (R (1)) и т. д.
Итак, мы определились: система Q (0) представляет конечное количество, система Q (0,1) — конечно-бесконечное (финфинитное) количество, где бесконечное представлено как модульное бесконечно большое Q (1). И данные определения возникают только в отношениях этих двух систем.
В современной версии математики нет конечно-бесконечного количества, но только либо конечное, либо бесконечное. Даже в концепте актуальной бесконечности, как было отмечено выше, нет конечных метрических определений. В системе Q (0,1) феномен конечно-бесконечного количества возникает именно из-за конечности интервала (-М,М), т.е. конечности числа М> 0, что позволяет всё конечное количество системы Q (0) представить как часть количества системы Q (0,1), определив последнее как конечно-бесконечное количество в отношении к системе Q (0). Таким образом, в основе феномена финфинитности лежит конечность числа М — верхнего порога обратной базовой R-функции.
Отсюда также становится понятным, как можно воспроизвести классические определения дихотомического количества, где внутренность и границы количества несоизмеримы до бесконечности. Для этого достаточно устремить М к нулю и в пределе получим бесконечно малый интервал (-М,М) и некоторый вырожденный вариант обратной базовой R-функции R-10, который отобразит множество R (0) в бесконечно малую окрестность нуля на R (1), что и должно быть в отношениях конечного и модульного бесконечно большого с точки зрения стандартного математического анализа. Тем самым мы выражаем некоторый принцип соответствия между представленной выше моделью с ненулевой конечной верхней границей М и классическим подходом с бесконечно малой границей.
Более-менее определившись со смыслом количественных систем Q (0), Q (1) и Q (0,1) и их отношением, вернёмся к теме того, как же можно задать алгебру на парах (х,у)?
Теперь мы понимаем, что элемент х выражает стандартное конечное количество, а элемент у — некоторый вид финфинитного количества, где бесконечное (инфинитное) представлено как модульное бесконечно большое, в пределе М→0 переходящее в обычное модульное бесконечно большое ±∞ для всего множества R (1).
Отсюда возникает естественная интерпретация пары (х,у) как суммы конечного и бесконечно большого элементов, что условно можно было бы выразить следующим образом: (х,у) = х + iy,
где iy — «интеграл у, т. е. представление у как элемента «интегральной шкалы» системы Q (0,1). Выражение iy можно понимать как домножение у на бесконечно большую единицу i.
Отсюда можно вывести следующие правила для операций на парах:
(х1,у1) + (х2,у2) = (х1 + iy1) + (х2 + iy2) = (х1 + х2) +
+ i (y1 + y2) = (x1+x2,y1+y2),
(х1,у1) ⋅ (х2,у2) = (х1 + iy1) ⋅ (х2 + iy2) = x1x2 + x1iy2 + x2iy1 +
+ i2y1y2 = x1x2 + x1iy2 + x2iy1 = x1x2 + i (x1y2 + x2y1) =
= (х1х2, x1y2 + x2y1).
Здесь было отброшено слагаемое i2y1y2, поскольку i2 — это бесконечно большая второго порядка, а в парах мы рассматриваем только бесконечно большие первого порядка.
На этой основе можно развить алгебру на парах, в том числе ограниченное деление пар, но в этой алгебре присутствуют делители нуля, так что мы не получим поля, но некоторую структуру, которую далее будем называть предполем.
Как интерпретировать пару (х,у) в связи со структурой количественной системы Q (0,1)?
В паре (х,у) элемент х берётся из множества R (0), а элемент у — из R (1). Но элементы х из R (0) одновременно представлены в интервале (-М,М) множества R (1). Поэтому элемент х можно интерпретировать и как элемент из R (0), и как элемент из R (1). В последнем случае такой элемент будет дан как величина х* = R-1М (х). Чтобы различать эти варианты, введём понятие 1-реализации пары (х,у) по правилу:
r1 (x,y) = y + R-1M (x).
Здесь обратная базовая R-функция играет роль как бы конечного дифференциала х, в отношении к которому величина у выступает как своеобразный интеграл, что и фиксируется в принятой выше интерпретации пары как х + iy.
6. О чёрно-белой и цветной математике
Надеюсь, читатель уже начинает чувствовать методологию R-анализа. В её основе лежит идея единства количества и качества. Мы рассматриваем не просто то или иное количество — множество натуральных, рациональных или вещественных чисел, — но задаёмся вопросом: какое качество мы связываем с тем или иным количеством, как скоординированы между собой количественные и качественные определения?
В стандартной математике — математике стандартного математического анализа — такого рода вопросы не возникают, поскольку либо работают с количеством одного качества, либо качества разных количественных систем слабо (конечно) отличаются друг от друга — что, например, имеет место для отношения качеств натуральных и целых чисел, целых и рациональных чисел. И только для вещественных чисел возникает некоторый более сильный скачок между качествами конечного и бесконечного, что и даёт новый потенциал развития математики. Но этот потенциал фиксируется в самом начале своей реализации и не разворачивается далее. R-анализ пытается реализовать этот потенциал количественно-качественных координаций как можно полнее.
Стоит отметить также ещё один момент.
Если смотреть на ряд координаций количества и качества, то с чисто количественной стороны в них исчезает какая-либо новизна. Например, рассмотренная выше методология построения количественных систем Q (0) и Q (0,1) с прообразным R (0) и образным R (1) множествами вещественных чисел превратится просто в некоторый вид отображения на вещественых числах, если не различать качества этих систем.
Переход к R-анализу не всегда сопровождается новой математической техникой, но всегда предполагает новое математическое мировоззрение, где старая математика начинает играть новыми смысловыми красками. И такими красками являются качества (слои), которые мы добавляем к чисто количественным определениям.
В этом смысле стандартная математика как бы чёрно-белая (не цветная). В ней господствует количество одного качества — в лице множества вещественных чисел, которое максимально вытесняет количества всех иных качеств. Если они и слабо мерцают в такой математике, то только вытесненные на бесконечно удалённые края господствующей системы конечного количества. Такую математику можно называть моноквантической — математикой одного количества (одной количественной системы).
В лице R-анализа мы начинаем иметь дело с «цветной» математикой — математикой количеств разных качеств и координацией их между собой. Такую математику можно называть поликвантической.
Когда мы начинаем раскрашивать количественные структуры в цвета разных качеств, то возникает новая организация, которая исчезает при чёрно-белом своём представлении. Поэтому важно встать на новую точку зрения поликвантизма и полихроматизма в теории количества, не редуцируя его только до количества одного качества-цвета. Последнее тоже возможно, и может быть полезно, но важно сохранять и цветовое многообразие количественных систем, наряду с монохроматическим подходом.
Например, на описанное выше преобразование обратной базовой R-функции R-1М:R→ (-М,М) можно посмотреть цветным зрением, и тогда мы увидим две количественные системы Q (0) и Q (0,1) со своими качествами конечного и модульного бесконечно большого, а можно посмотреть чёрно-белым зрением и увидеть за R (0) и R (1) всего лишь одно и то же множество вещественных чисел с одним качеством конечного. В последнем случае мы потеряем конструкции R-анализа и вновь скатимся в стандартную моноквантическую математику. Поэтому важно изменить ещё и систему смыслов в своём математическом сознании, даже работая со стандартной математической техникой, — и тогда она заиграет новыми красками и смыслами.
Конечно, R-анализ будет давать и новую математическую технику, связанную с идеей поликвантизма. Но первые его шаги могут протекать ещё в рамках старой техники, лишь требуя нового цветного зрения. И это важно понять и удержать такую способность, чтобы суметь пройти эти первые шаги, не скатиться в чёрно-белый моноквантизм и достичь царства цветной математики.
Путеводная нить Ариадны в лабиринтах новой математики — это идея количественной системы как единства количественно-качественных определений. Мы теперь не просто работаем с количеством, но со множеством количеств разных качеств, и границы количественных систем и их качеств определяют R-функции. Далее мы смотрим на возникающие здесь координации, исследуем их и выражаем в новых (или старых) операциональных средствах.
7. Новая модель бесконечно малого количества
Обратная базовая R-функция позволила нам ввести бесконечно большое как актуальную величину, в том числе с конечной внешней метрикой. Как теперь мы могли бы ввести бесконечно малое в качестве аналогичной актуальной величины?
Вернёмся к идее бесконечно малого в математическом анализе.
Здесь, как уже отмечалось, бесконечно малая — это бесконечная последовательность вещественных чисел, имеющая пределом ноль. Согласно линии Лейбница, ненулевые бесконечно малые лежат между нулём и всеми конечными вещественными числами. В нестандартном анализе область бесконечно малых представлена как бесконечно малая окрестность нуля в рамках множества гипердействительных чисел. Кстати, в честь Лейбница, такая бесконечно малая окрестность нуля получила название монады.
Иными словами, если мы возьмём некоторый супермикроскоп и посмотрим на ноль на шкале вещественных чисел, то увидим там целый мир — монаду нуля, в которой расположено множество бесконечно малых чисел (см. рис. 4).
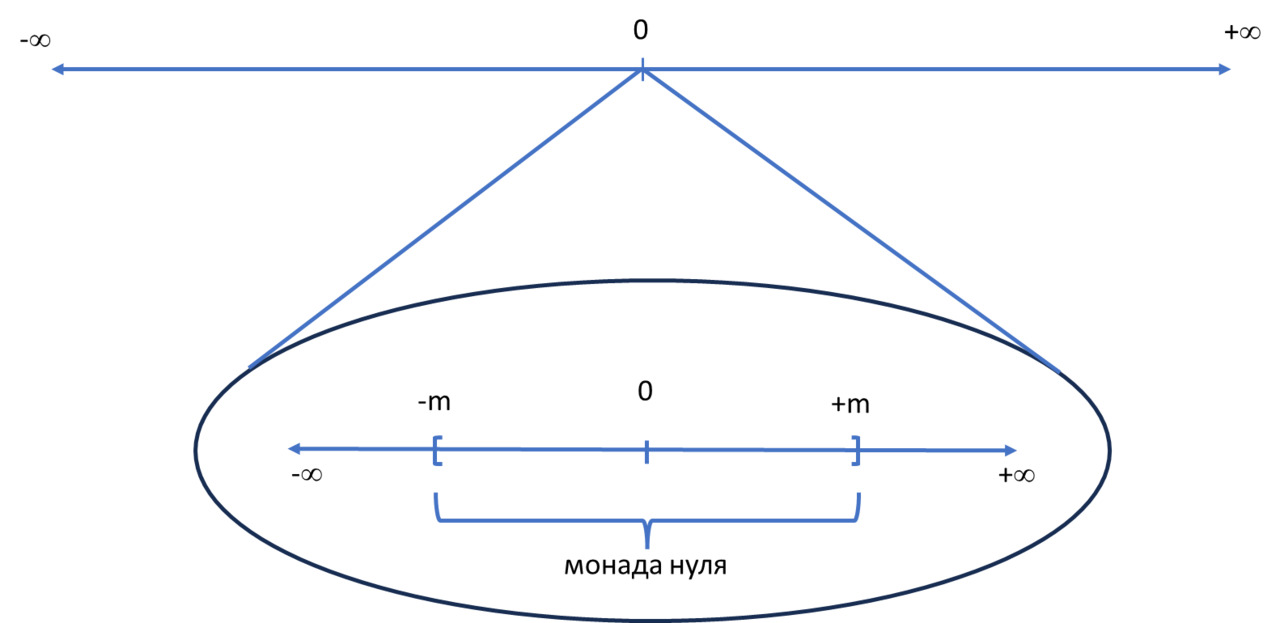
Опять мы встречаем здесь процедуру финитизации (оконечивания) бесконечного. Но если в случае бесконечно больших величин происходила их финитизация до конечных чисел, то в случае бесконечно малых наш супермикроскоп оконечивает область бесконечно малых величин. И если финитизацию бесконечно большого выполняла обратная базовая R-функция, то как реализовать финитизацию бесконечно малых?
Такую финитизацию не может выполнить обратная базовая R-функция, поскольку она конечному сопоставляет только конечное. А нам нужно какое-то отображение, которое бы бесконечно малому сопоставило конечное.
Применим для решения этой задачи вновь методологию координации количества и качества.
Бесконечно малые величины — это количество иного качества, нежели конечные величины. Бесконечно малые обладают качеством бесконечной малости. Конечные величины имеют качество конечного. Это значит, что они принадлежат к разным количественным системам, каждая со своим качеством-слоем. Эти системы скоординированы между собой, но внутри себя они устроены изоморфно. Следовательно, мы вновь можем представить их парами (х,у), где х — элемент конечной количественной системы Q (0), у — элемент бесконечно малой системы, которую обозначим как Q (-1).
Алгебру на таких парах мы можем задать аналогично той алгебре, которая была описана выше, с той лишь особенностью, что второй элемент пары выступает не как бесконечно большое, а как бесконечно малое, что можно выразить таким образом: (х,у) = х + dy, где dy — «дифференциал у», но в смысле домножения у на бесконечно малую единицу d.
Операции на таких парах можно определить аналогично операциям на интегральных парах, везде заменяя i на d, например:
(х1,у1) + (х2,у2) = (х1 + dy1) + (х2 + dy2) = (х1 + х2) + d (y1 + y2) =
= (x1+x2,y1+y2),
(х1,у1) ⋅ (х2,у2) = (х1 + dy1) ⋅ (х2 + dy2) = x1x2 + x1dy2 + x2dy1 +
+ d2y1y2 = x1x2 + x1dy2 + x2dy1 = x1x2 + d (x1y2 + x2y1) =
= (х1х2, x1y2 + x2y1).
Здесь был отброшено слагаемое d2y1y2, поскольку d2 — это бесконечно малая второго порядка, а в парах мы рассматриваем только бесконечно малые первого порядка.
Но как быть с R-функцией?
По аналогии с обратной базовой R-функцией мы можем ввести обратную монадическую R-функцию, R-1m, m> 0, которая будет сжимать множество бесконечно малых R (-1) в интервал (-m,m) на множестве конечных величин R (0). Внутри себя множество бесконечно малых R (-1) — то же множество вещественных чисел, что и R (0) (см. рис. 5).
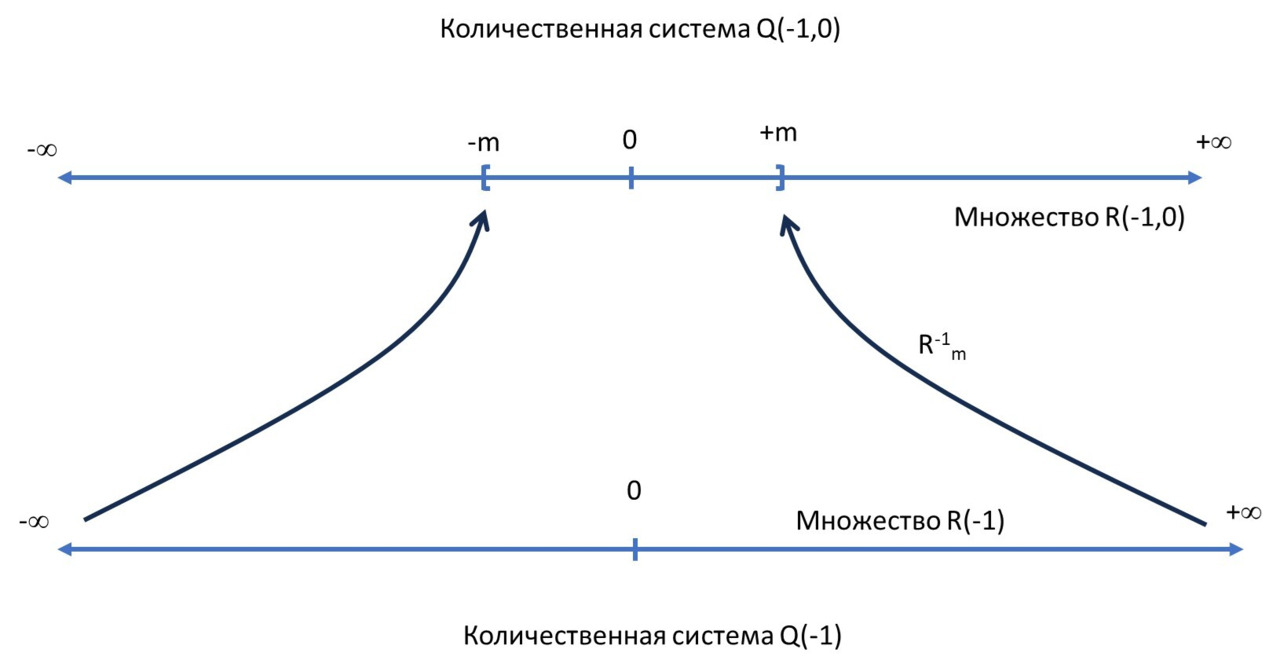
Таким образом, подобно тому как мы сжимаем обратной базовой R-функцией множество конечных чисел в конечный интервал на множестве бесконечно больших чисел, подобно этому мы сжимаем обратной монадической R-функцией множество бесконечно малых чисел в конечный интервал на множестве конечных чисел. Особенность в том, что сжатие происходит относительно множества бесконечно малых чисел, данных изнутри себя как обычное множество вещественных чисел. Такое множество R (-1) можно называть прообразным множеством бесконечно малых. Интервал (-m,m) по-прежнему можно называть «монадой». Случай нестандартного анализа будет получен в пределе стремления верхнего порога монадической R-функции m к нулю.
Когда мы проецируем множество бесконечно малых у∈R (-1) на множество конечных чисел R (0), получая монаду нуля (-m,m), то данный интервал выражает момент изоморфизма между бесконечно малыми и частью конечных величин х∈R (0), попадающих в этот интервал. По аналогии с интервалом (-М,М) на множестве R (1), в рамках которого возникает конечный аспект конечно-бесконечного количества системы Q (0,1), — точно таким же образом интервал (-m,m) на множестве R (0) выражает бесконечно малый аспект нового состояния количества, совмещающего в себе моменты бесконечно малого и конечного. В итоге мы проекцией множества R (-1) на множество R (0) меняем качество последнего — из просто конечного количества оно переходит в разряд конечно-бесконечного (финфинитного) количества, соединяя в себе конечное и бесконечно малое. Такую количественную систему можно обозначить как Q (-1,0).
Таким образом, количественная система Q (0) — это система конечного количества, в которой нет конечной монады нуля, а система Q (-1,0) — система конечного количества, которое стало соизмеримым с бесконечно малым количеством в рамках конечного интервала (-m,m), и поэтому это уже не совсем конечное количество, но конечно-бесконечное состояние количества, где бесконечный его аспект представлен бесконечно малым количеством в рамках конечной монады нуля.
Далее центр монады нуля можно сдвинуть в любую точку х∈R (0), и мы получим монаду с центром в х: (х-m,x+m). В этом случае множество прообразных бесконечно малых R (-1) будет проецироваться в данный интервал той же обратной монадической R-функцией R-1m, но сдвинутой на величину х, т.е. х + R-1m (y).
В итоге всё множество R (0) покроется конечными интервалами (х-m,x+m), и именно такую структуру количества мы будем понимать как количественную систему Q (-1,0), а не только содержащую лишь монаду нуля. Множество R (0), покрытое монадами для каждой точки х∈R (0), можно теперь обозначать как множество R (-1,0).
Как интерпретировать пару (х,у) в связи со структурой количественной системы Q (-1,0)?
В паре (х,у) элемент х берётся из множества R (0), а элемент у — из R (-1). Но элементы у из R (-1) одновременно представлены в интервале (x-m,x+m) множества R (-1,0). Поэтому элемент y можно интерпретировать и как элемент из R (-1), и как элемент из R (-1,0). В последнем случае такой элемент будет дан как величина y* = R-1m (y). Чтобы различать эти варианты, введём понятие (-1) -реализации пары (х,у) по правилу:
r-1 (x,y) = x + R-1m (y).
Здесь обратная монадическая R-функция играет роль как бы конечного дифференциала y, что и фиксируется в принятой выше интерпретации пары как х + dy.
8. Симметричные и иерархические отношения бесконечно большого и бесконечно малого
Благодаря R-функциям, мы можем строить новый вид количественных систем, которые соединяют в себе конечное и бесконечное как конечно-соизмеримые состояния. Таковы, например, количественные системы Q (0,1) и Q (-1,0). В первой из них соизмеряются конечное и модульное бесконечно большое количество, во второй — конечное и бесконечно малое количество. Алгебры этих систем представлены выше как алгебры пар.
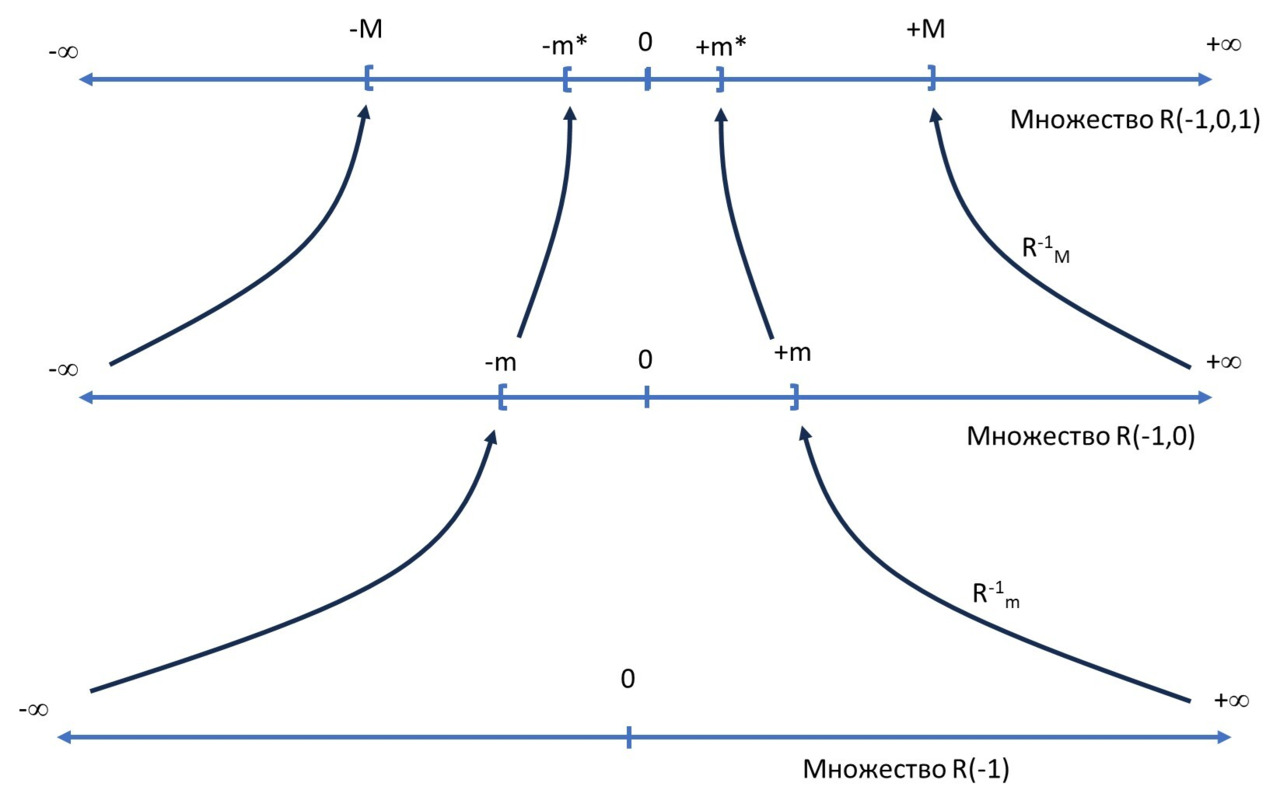
Сделаем следующий шаг и скоординируем между собой три количественные системы — бесконечно малого, конечного и бесконечно большого количества.
Для этого начнём с количественной системы Q (-1,0), которая координирует в себе конечное и бесконечно малое в рамках множества R (0), каждая точка х из которого является центром монады (x-m,x+m), — такое множество теперь точнее обозначить как R (-1,0); а затем, как и ранее, сожмём множество R (-1) обратной базовой R-функцией в интервал (-М,М) на множестве R (1). В итоге каждая сумма х+R-1m (y) из множества R (-1,0) будет представлена как величина
R-1М (х+R-1m (y)).
Заметим далее симметрию между бесконечно малым, конечным и бесконечно большим: бесконечно малое так относится к конечному, как конечное к бесконечно большому.
Более конкретно эту симметрию можно теперь реализовать так, что на множестве R (1) мы можем сжать множество R (0) не только в окрестности нуля — в виде интервала (-М,М), — но образовать такие интервалы вокруг любой точки р∈R (1), используя обратную базовую R-функцию р + R-1М. Это тот же приём, что мы использовали, сдвигая монаду нуля в любую точку х∈R (0). Интервал (-М,М) — тоже своеобразная «монада», но в которой сжата область не бесконечно малого, а конечного количества на шкале бесконечно большого количества. Сдвигая центры интервала (-М,М) в любую точку р∈R (1), мы получаем суммы р+R-1М (х), а учитывая, что ещё ранее мы образовали не просто величины х∈R (0), а также суммы х + R-1m (y) из R (-1,0), в итоге получим суммы вида
р + R-1М (х+R-1m (y)),
которые можно рассматривать как 1-реализации троек (р,х,у):
r1 (p,x,y) = р + R-1М (х+R-1m (y)) (см. рис. 6).
Как определить алгебру на таких тройках?
С одной стороны, мы могли бы соединить две интерпретации, представленные выше для пар конечных величин с бесконечно малыми и бесконечно большими, тогда получим такое представление тройки (назовём его симметричным):
(р,х,у) = ip + x + dy.
С другой стороны, элементы i и d таковы, что их произведение должно быть равно единице, т.е. id = 1, и здесь предполагается мультипликативная симметрия бесконечно большого и малого относительно конечного количества. Но в 1-реализации тройки r1 (p,x,y) мы видим структуру не столько симметрии в организации количества относительно центра конечного количества, сколько идею иерархии бесконечно большого, конечного и бесконечно малого. Как операционально реализовать такую иерархию?
Мультипликативная симметрия выражается в том, что возникают как бы степени разных знаков, когда мы можем использовать следующие соотношения
i = d-1,
d = i-1,
1 = d0 = i0.
Чтобы избавиться от степеней разных знаков и перевести их в степени одного знака, вынесем за скобки множитель с минимальной степенью (такую интерпретацию тройки можно называть интегральной):
(р,х,у) = ip + x + dy = d (i2p + ix + y)
и определим операции на тройках, выводя этот множитель за все операции и проводя их только с элементами внутри скобок:
(р1,х1,у1) + (р2,х2,у2) = d (i2p1 + ix1 + y1) + d (i2p2 + ix2 + y2) =
= d (i2p1 + ix1 + y1 + i2p2 + ix2 + y2) = d ((i2p1 + i2p2) +
+ (ix1 + ix2) + (y1 + y2)) = d (i2 (p1 + p2) + i (x1 + x2) + (y1 + y2)) =
= (p1+p2,x1+x2,y1+y2),
(p1,х1,у1) ⋅ (p2,х2,у2) = d (i2p1 + ix1 + y1) ⋅ d (i2p2 + ix2 + y2) =
= d (i2p1 + ix1 + y1) ⋅ (i2p2 + ix2 + y2)) = d (i2p1⋅ i2p2 + i2p1⋅ ix2 +
+ i2p1м⋅y2 + ix1⋅i2p2 + ix1⋅ix2 + ix1⋅ y2 + y1⋅i2p2 + y1⋅ix2 + y1⋅y2) =
= d (i2p1 ⋅ y2 + i2x1x2 + ix1y2 + i2p2y1 + ix2y1 + y1y2) = d (i2 (p1y2 +
+ x1x2 + p2y1) + i (x1y2 + x2y1) + y1y2) = (p1y2 + x1x2 + p2y1, x1y2 +
+ x2y1, y1y2).
При проведении этих преобразований мы по-прежнему отбрасываем степени бесконечных, выходящие за используемую интерпретацию (в данном случае это степени бесконечно большого, выше двух) и используем степенные соглашения для коэффициентов ikdm = ik-m = dm-k, где i0 = d0 = 1.
Давайте сравним это с операциями, если бы мы брали симметричную интерпретацию тройки как (р,х,у) = ip + x + dy. В этом случае мы бы получили:
(р1,х1,у1) + (р2,х2,у2) = (ip1 + х1 + dy1) + (ip2 + х2 + dy2) =
= i (p1+p2) + (х1 + х2) + d (y1 + y2) = (p1+p2,x1+x2,y1+y2),
(p1,х1,у1) ⋅ (p2,х2,у2) = (ip1 +х1 + dy1) ⋅ (ip2 +х2 + dy2) =
= i2p1p2 + ip1x2 + ip1dy2 + x1ip2 + x1x2 + x1dy2 + dy1ip2 +
+ x2dy1 + d2y1y2 = i (p1x2 + x1p2) + (p1y2 + x1x2 + y1p2) +
+ (x1dy2 + x2dy1) = (p1x2 + x1p2, p1y2 + x1x2 +
+ y1p2, x1y2 + x2y1).
Таким образом, на сложении (и вычитании) это бы не сказалось, а вот для умножения получаем разницу.
Причём, заметим, что исключить мультипликативную симметрию мы можем не только вынесением за скобки самой малой степени, но и самой большой. Тогда мы могли бы использовать такую интерпретацию тройки (назовём её дифференциальной):
(р,х,у) = ip + x + dy = i (p + dx + d2y),
и для такой интерпретации мы получили бы для умножения ещё третий вариант:
(p1,х1,у1) ⋅ (p2,х2,у2) = i (p1 + dx1 + d2y1) ⋅ i (p2 + dx2 + d2y2) =
= i ((p1 + dx1 + d2y1) ⋅ (p2 + dx2 + d2y2)) = i (p1p2+ p1dx2 + p1d2y2 +
+ dx1p2 + dx1dx2 + dx1d2y2 + d2y1p2 + d2y1dx2 + d2y1d2y2) =
= i (p1p2+ d (p1x2 + x1p2) + d2 (p1y2 + x1x2 + y1p2)) = (p1p2, p1x2 +
+ dx1p2, p1y2 + x1x2 + y1p2).
Что делать со всеми этими вариантами интерпретации тройки и умножения, какой из них выбрать?
Во-первых, следует отметить, что случай интегральной интерпретации
(р,х,у) = d (i2p + ix + y)
соответствует случаю симметричной интерпретации пятёрки
(p,x,y,z,t) = i2p + ix + y + dz + d2t
при z = t = 0.
Аналогично, случай дифференциальной интерпретации тройки
(р,х,у) = i (p + dx + d2y)
соответствует симметричной интерпретации пятёрки
(s,q,p,x,y) = i2s + iq + p + dx + d2y
при s = q = 0.
В итоге несимметричные (дифференциальную и интегральную) интерпретации тройки мы можем свести к симметричной интерпретации пятёрки, обнуляя в ней два дифференциальных, либо два интегральных элемента.
Приведённая выше 1-реализация тройки r1 (p,x,y) = р + R-1М (х+R-1m (y)) соответствует такому представлению, при котором бесконечно большое количество выступает как конечное, конечное — как бесконечно малое первого порядка, и бесконечно малое — как таковое второго порядка, что связано с дифференциальной интерпретацией тройки (р,х,у) = i (p + dx + d2y).
Заключая, мы видим, что 1) возможны как симметричные, так и несимметричные (иерархические) интерпретации троек, 2) несимметричные интерпретации троек можно свести к симметричным, расширяя тройки до пятёрок, 3) с каждой интерпретацией, по-видимому, должны быть связаны свои представления троек через R-функции.
В целом, контуры аппарата R-анализа начинают расширяться, и мы стоим на пороге некоторого более глобального обобщения всех тех частных конструкций, которые были представлены до сих пор.
9. Обратное сложение
Обратимся ещё раз к теме мультипликативной симметрии между интегральным и дифференциальным количеством. Если брать символ бесконечно большого числа ∞ и бесконечно малого 1/∞, то между ними дана явная мультипликативная симметрия: бесконечно малое есть величина, обратная к бесконечно большому.
Но если мы возьмём некоторую дифференцируемую функцию f (x), то её производная df/dx и интеграл F (x) = ∫f (x) dx уже не обнаруживают такой симметрии. В то время как бесконечно большая р и бесконечно малая у координаты в тройке (р,х,у), если смотреть на алгебру троек (р,х,у) = ip + x + dy, ведут себя симметрично.
Это значит, что обычные производная и интеграл построены в стандартном анализе скорее в рамках несимметричных интерпретаций троек — как (р,х,у) = i (p + dx + d2y) или (р,х,у) = d (i2p + ix + y). В то же время возможна также симметричная интерпретация троек.
Будем далее использовать операцию обратного сложения +*: х +*у = (х-1 + у-1) -1.
Можно показать, что для этой операции выполняются требования группы, где противоположным элементом для х является -х, но роль нейтрального элемента играет не ноль 0, а бесконечность ∞, если принять, что 0 = 1/∞. В самом деле:
Коммутативность: х +* у = (х-1 + у-1) -1 = (у-1 + х-1) -1 = у +*х,
Ассоциативность: ((х+*у) +*z) = (((х-1+у-1) -1) -1+ z-1) -1 =
= ((х-1+у-1) + z-1) -1 = (х-1 + (у-1+z-1)) -1 = (х-1+ (((у-1+z-1) -1) -1) -1 =
= (х +* (у +* z)),
Нейтральный элемент: x +*∞ = (x-1 + ∞-1) -1 = (x-1 +0) -1 =
= (x-1) -1 = x,
Противоположный элемент: x +* (-x) = (x-1+ (-x) -1) -1 =
= (x-1 — x-1) -1 = 0—1 = ∞.
Что касается взаимодействия операции +* и умножения, то здесь выполняется свойство дистрибутивности, как и для обычного сложения:
Дистрибутивность: z (x +* y) = z ((x-1 + y-1) -1) = z/ ((1/x) +
+ (1/y)) = z/ ((x+y) /xy) = 1/ ((x+y) /zxy) = ((x+y) /zxy) -1 =
= ((x/zxy) + (y/zxy)) -1 = ((zy) -1 + (zx) -1) -1 = zx +* zy.
Введём также порядок <* по правилу:
х <*у е. т. е. х-1 <у-1.
Это означает переворачивание порядка:
х <*у е. т. е. х> у,
так что будем называть порядок <* обратным порядком.
В рамках обратного порядка <* элемент ∞ является минимальным среди всех неотрицательных элементов, а элемент 0 — максимальным (причём, начнут различаться +0 и -0).
В итоге мы можем построить поле на вещественных числах с операциями обратного сложения +* и обычного умножения.
Введением тройки (р,х,у) и её симметричной интерпретацией мы предполагаем такую числовую структуру, когда есть некоторое центральное количество х и относительно него определяется не только дифференциальное, но и интегральное количество. Но если интерпретацию дифференциального количества можно представить как дифференциальное приращение х+dx, которое добавляется к х — центру монады, то как представить реализацию интегрального количества, которое точно так же должно добавляться к конечному количеству х?
Первый шаг в ответе на этот вопрос — введение операции обратного сложения и связанной с ним структуры. Но чтобы сделать второй шаг и более глубоко понять реализацию бесконечно большого относительно конечного, нам нужно будет рассмотреть новый концепт так называемого «обратного количества».
10. Обратное количество
Как мы видели ранее, в отношениях бесконечно большого ∞ и бесконечно малого 1/∞ важную роль играет мультипликативная инверсия. Далее такую инверсию можно продолжить на операции, введя обратное сложение +*. В этом случае величины х и у будут вести себя как 1/х и 1/у.
Отсюда видна двойственность вещественного числа х: в операции обычного («прямого») сложения число х выступает как таковое, а в операции обратного сложения — как 1/х. В самом деле:
х +* х = (х-1 + х-1) -1 = (2 (х-1)) -1 = х/2.
Обратное сложение приводит не к увеличению суммы, а к её уменьшению — словно количественный процесс движется в обратном направлении. И если в прямом количестве рост величины идёт от нуля к бесконечности, то в обратном сложении как бы в обратную сторону — от бесконечности к нулю. Всё это позволяет ввести концепт обратного количества — количества, растущего в обратном направлении, не от нуля к бесконечности, а обратно — от бесконечности к нулю.
Но тогда смысл прямого и обратного количества затрагивает не только операции, но и само количество, в конечном итоге — каждую величину, представленную тем или иным вещественным числом.
Пусть дано некоторое вещественное число х> 0. На числовой прямой мы выражаем его отрезком [0,x] с началом в нуле и концом в точке х. И тогда рост такого числа — это увеличение отрезка, т.е. всё большее движение конца отрезка вправо. Так определяется прямое количество.
Если же рост обратного количества должен всё больше приближать к нулю, то величина х должна быть концом такого отрезка, рост которого будет приближать его конец к нулю, а не бесконечности. Если конец такого отрезка будет по-прежнему лежать в точке х, то где будет его начало? Роль нуля на шкале обратного сложения играет бесконечность ∞. Тогда остаётся предположить, что величина х может выражать не только отрезок [0,x], но и отрезок [x,∞], рост которого начнёт приближать точку х к нулю.
Тем самым одна и та же точка х может выражать конец двух отрезков — прямого отрезка [0,x] и обратного отрезка [x,∞]. Рост первого будет сдвигать точку х вправо, к бесконечности, а рост второго сдвигает точку х влево, к нулю.
За этой пока формальной симметрией видится глубокая идея двух видов количества — прямого и обратного. Количество может расти как в прямом направлении — от нуля к бесконечно большому, так и в обратном направлении — от бесконечно большого к нулю.
В этом случае ноль 0 и бесконечность ∞ выступают как бы двумя полюсами количества, от которых количество может расти или к которым оно может стремиться. До сих пор математика использовала только концепт прямого количества. Пора начать работать с конструкциями обратного количества. Посмотрим, что из этого получится.
Итак, одно и то же число х> 0 может как выражать прямое количество, растущее от нуля, — обозначим такое понимание х как х0, так и выражать количество, растущее от бесконечности — пусть это будет х∞. Индексами справа внизу мы изображаем те полюсы, от которых растёт соответствующее количество (см. рис. 7).

Причём, если мы теперь берём число х∞ и складываем его с собой обратным сложением, то получаем величину (х/2) ∞:
х∞ +*х∞ = (х+*х) ∞ = (х/2) ∞.
Такой взгляд содержит в себе некоторую гетерономность — мы смотрим на обратное количество глазами прямого количества и обратно-растущее воспринимаем как прямо-уменьшающееся. Более последовательным будет в этом случае полный переход на точку зрения «обратной перспективы» — перспективы обратного количества, где ∞ — это 0. Но тогда и число х будет дано в этой обратной перспективе как х-1.
Зафиксируем такой переход на собственную точку зрения обратного количества в следующей символике:
х∞ ≈ ∞ (х-1),
где ≈ — некоторое отношение m-симметрии, определяемое по правилу х≈у е.т.е х=у-1 и учитывающее символику полюсов, которая определяется так, что величина х∞ — это величина, которая начинается в полюсе бесконечности ∞ и заканчивается в точке х, отсчитываемой от нуля, а ∞х — это величина обратного количества, имеющая метрику х в системе этого количества.
Те же идеи можно выразить введением 0-метрики и ∞-метрики на полюсных величинах х0 и х∞:
ρ0 (х0) = |x-0| = |x|,
ρ0 (х∞) = |x- ∞| = |∞|,
ρ∞ (х∞) = |x-1- ∞-1| = |x-1|,
ρ∞ (х0) = |x-1-0-1| = |∞|.
Тогда переход от х∞ к ∞ (х-1) — это переход от 0-метрики к ∞-метрике величины х∞, т.е. мы начинаем видеть величину х∞ в собственной перспективе обратного количества, и в этой обратной перспективе х∞ имеет величину х-1, что и фиксируется выражением ∞ (х-1).
Таким образом, запись х∞ — это некоторое смешанное представление, когда на обратное количество, которое имеет величину х-1 в своей собственной системе, мы смотрим глазами прямого количества. В итоге, одна и та же точка х на числовой прямой может выражать как прямое количество х0, так и обратное количество х∞, которое в своей системе предстаёт как величина ∞ (х-1).
Описанные выше конструкции могут быть распространены на отрицательные величины х <0, т.е. их также можно записать в виде х∞, но теперь в качестве полюса бесконечности, от которого они откладываются, следует понимать величину -∞.
Вообще, здесь следует заметить, что в системах прямого и обратного количества полюсы бесконечности и нуля эквивалентны. Это, в частности, означает, что как -0 = +0 и -∞ ≠ +∞ в системе прямого количества (которое ещё можно называть 0 — количеством), так же в системе обратного количества (∞ — количества) имеем +∞ = -∞, но -0 ≠ +0.
Это заставляет нас обратить внимание на равенства, вводя также два их вида:
х0 =0 у0 е.т.е. х=у
х∞ = ∞у∞ е.т.е. х-1 = у-1.
Кажется, что случай х-1 = у-1 равносилен х=у, но это верно лишь до тех пор, пока мы не взяли в качестве х и у либо ±0, либо ±∞. Например, хотя -0 = +0, но -∞ ≠ +∞ и т. д.
Теперь окинем общим взглядом, что мы сделали, вводя концепты прямого и обратного количества.
Мы построили множество R-1, изоморфное множеству вещественных чисел R, но перевёрнутое по ролям нуля и бесконечности: роль нуля 0 из R во множестве R-1 играет бесконечность ∞ и наоборот. Основа этого изоморфизма — отображение мультипликативной симметрии (инверсии)
Inv (x) = x-1.
В терминах оператора Inv обратное сложение +* можно представить таким образом:
х +* у = Inv (Inv (x) + Inv (y)).
Для пересчёта метрики ∞ -величин можно записать:
х∞ ≈ ∞Inv (x).
Далее вернёмся к исследованию следующего вопроса: связаны ли все эти темы прямого и обратного количества со структурами R-анализа, и если да, то каким образом?
11. Операторы инверсии
Конструкции R-анализа, как ни странно, заложены уже в операторе мультипликативной инверсии Inv (x) = 1/x, потому что этот оператор делает бесконечное конечным, Inv (∞) = 0, и конечное — бесконечным: Inv (0) = ∞ Но нечто подобное делают и R-функции: прямая R-функция отображает конечное в бесконечное, обратная R-функция — бесконечное в конечное. Как было замечено ранее, бесконечное — это граница количественной системы, где она граничит с количеством другого качества, и достижение границы — уже некоторый эффект встречи двух количественных систем.
Остаётся теперь более операционально выразить связь мультипликативной инверсии и связанных с нею конструкций обратного количества со структурами R-анализа.
Переход на точку зрения обратного количества делает полюс бесконечности нулём — разновидностью конечного количества. Чтобы сделать полюс бесконечности конечным, с ним нужно начать оперировать как с конечным числом, в связи с чем можно предположить, что оператор мультипликативной инверсии имеет такой вид:
Inv (x) = AoR-1M (x),
где о — операция композиции операторов, R-1М — обратная R-функция с некоторым верхним порогом М, и А — некоторый оператор. Теперь вопрос в том, что это за оператор А?
Рассмотрим вновь для простоты некоторое положительное вещественное число х> 0. Когда мы подействуем на множество вещественных чисел R обратной R-функцией R-1М, получим интервал (-М,М), и число х перейдёт в число х* = R-1М (х), которое будет лежать между нулём 0 и М.
Точка х* также может выражать два вида количества — прямое, отсчитываемое от нуля х*0, и обратное, отсчитываемое от М, что можно обозначить как х*М, поскольку полюс бесконечности ∞ действием обратной R-функции финитизирован до конечного числа М = R-1М (∞) (см. рис. 8).
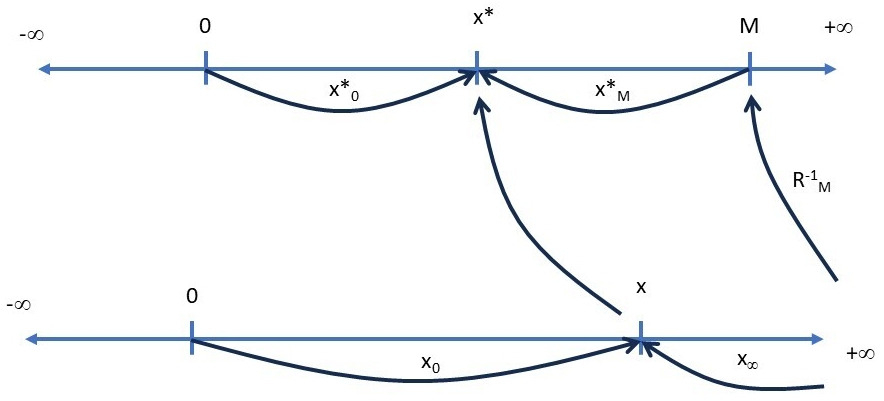
Тогда прямое количество х*0 будет выражаться величиной отрезка [0,x*], а обратное количество х*М — величиной отрезка [x*,M]. Посмотрим на длины этих отрезков:
| [0,x*] | = x*,
| [x*,M] | = M-x*.
Величина М-х* — это величина обратного количества х*М в собственной количественной системе, когда величины отсчитываются от полюса бесконечности. Но в обычном множестве вещественных чисел мы не могли прямо измерить эту величину, потому что полюс бесконечности был в самом деле бесконечен. Теперь же он финитизирован обратной R-функцией и представлен как конечное число М = R-1М (∞), и мы можем прямо определить величину обратного количества. По аналогии с записью
х∞ ≈ ∞ (х-1),
можем записать:
х*М ≈ М (М-х*),
где М (М-х*) — представление числа х*М в собственной М-метрике, отсчитываемой от М.
Таким образом, числа х и х-1, связанные мультипликативной инверсией на обычной шкале вещественных чисел, в случае R-шкалы (-М,М) представляются числами х*0 и х*М с величинами х* и М-х* соответственно.
Обозначим разность М-х* в качестве оператора М-дополнения
DM (x*) = M-x*.
Тогда представление оператора мультипликативной инверсии Inv мы можем сделать ещё более определённым:
Inv (x) = BoDMoR-1M (x),
т.е. оператор Inv мы теперь представляем как композицию трёх операторов — обратной R-функции R-1М, оператора М-дополнения и некоторого оператора В.
Остаётся определить, что это за оператор В?
Заметим, что оператор Inv действует на обычном множестве вещественных чисел, а после действия двух операторов R-1М и DM мы пока находимся в R-множестве (-М,М). Поэтому нам нужно вернуться от этого множества к обычному множеству вещественных чисел, что делает прямая R-функция R+1М. Отсюда возникает гипотеза, что оператор В равен прямой R-функции с тем же верхним параметром М, и в целом оператор m-инверсии примет вид:
Inv (x) = R+1M (x) oDMoR-1M (x).
Остаётся подобрать такую R-функцию, чтобы выполнялось соотношение
Inv (x) = R+1M (x) oDMoR-1M (x) = х-1.
Такая R-функция в самом деле существует, и в своей монографии «Логика открытого синтеза» я её приводил. Она имеет следующий вид (при М=2):
— обратная R-функция:
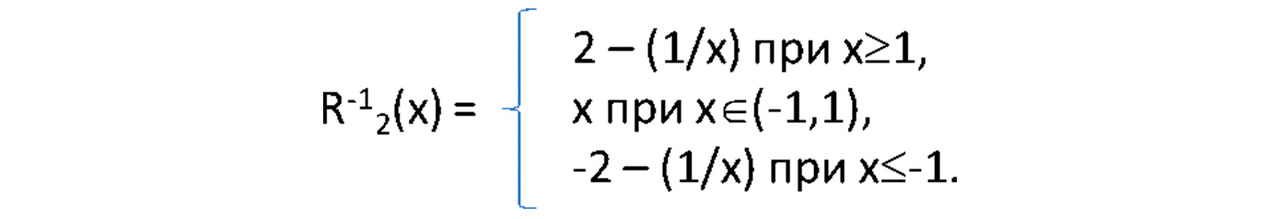
— прямая R-функция:
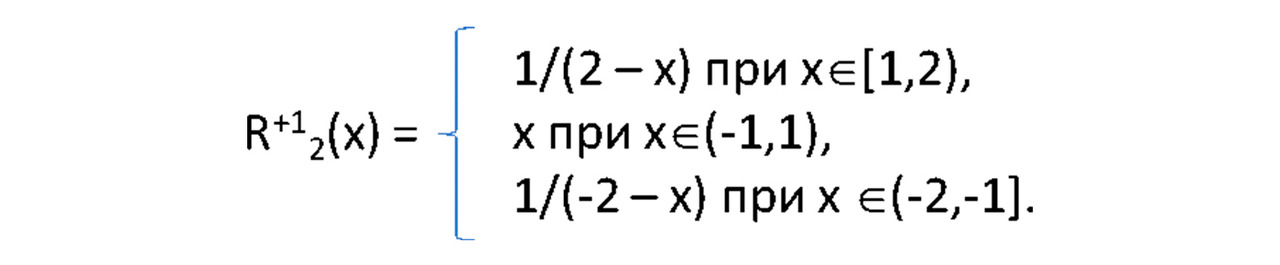
Хотя эти функции составлены из трёх кусков, но они не только непрерывные, но и гладкие, поскольку левые и правые производные равны в точках х = ±1.
Также следует расширить оператор М-дополнения на отрицательные значения:
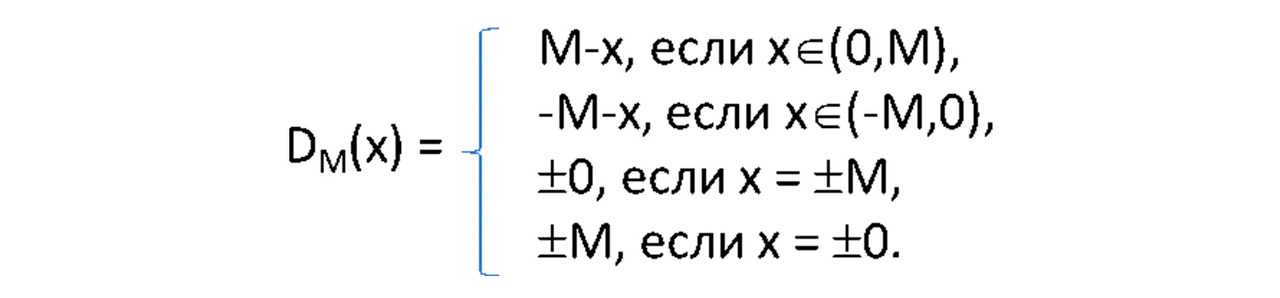
Поскольку оператор М-дополнения работает с R-образами прямых и обратных величин, а у обратных величин различаются +0 и -0 — как у прямых величин различаются +∞ и -∞, — то в качестве аргументов оператора М-дополнения введены в том числе элементы +0 и -0. И, например, запись «±0, если х=±М» следует понимать как сокращение для выполнения двух условий: 1) +0, если х=+М, и 2) -0, если х=-М.
Проверим, что 1/х = Inv (x) = R+1M (x) oDMoR-1M (x) для приведённых выше R-функций R±12 на примере величины х∈ (1,2). Здесь имеем:
R-12 (х) = 2 — 1/х,
D2 (2 — 1/х) = 1/x <1,
R+12 (1/х) = 1/x.
Аналогично можно показать выполнение остальных случаев.
Таким образом, мы в самом деле можем доказать, что оператор мультипликативной инверсии Inv оказывается тесно связан с R-функциями, т.е. за операцией взятия обратного количества х-1 стоит более глубокая R-структура. Запрет деления на ноль — это по сути запрет на выход в другую количественную систему обратного количества х∞.
Более того, показав связь оператора Inv со специфической R-функцией, мы можем оторваться от этой специфики и обобщить оператор мультипликативной инверсии Inv до оператора обощённой инверсии Iv, для определения которого используем ту же формулу
Iv (x) = R+1M (x) oDMoR-1M (x),
но теперь предполагая возможность использования любых R-функций в данном определении.
Заметим также, что выполняется следующее соотношение:
IvoIv (x) = x,
если ещё ранее принимать во внимание, что
DMoDM (x*) = x*.
Также имеем:
Iv (∞) = R+1M (x) oDMoR-1M (∞) = R+1M (x) oDM (M) = R+1M (0) = 0,
где ∞ = ±∞ для обратных величин (как и ± 0 = 0 для прямых величин).
Покажем также выполнение свойства
Iv (-x) = -Iv (x).
В самом деле, функции R±1М являются нечётными, тогда нужно проверить нечётность только оператора М-дополнения. Здесь имеем:
1) х∈ (0,М), тогда -x∈ (-M,0) и DM (-x) = -М- (-х) = -М+х =
= — (М-х) = -DM (x),
2) х∈ (-М,0), тогда -x∈ (0,M) и DM (-x) = М- (-х) = М+х=
= — (-М-х) = -DM (x),
3) х = +0, тогда -x = -0, и DM (-x) = DM (-0) = -M =
= -DM (+0) = -DM (x),
4) х = -0, тогда -x = +0, и DM (-x) = DM (+0) = +M =
= -DM (-0) = -DM (x),
5) х = +M, тогда -x = -M, и DM (-x) = DM (-M) = -0 =
=-DM (+M) = -DM (x),
6) х = -M, тогда -x = +M, и DM (-x) = DM (+M) = +0 = -DM (-M) =
= -DM (x).
Таким образом, доказано, что оператор М-дополнения также является нечётным, т.е. все операторы в определении оператора обобщённой инверсии Iv — нечётные. Следовательно, и сам оператор Iv также нечётный.
На этой основе можно проверить, что для операции обратного сложения
х +*у = Iv (Iv (x) + Iv (y)),
но сформулированной теперь для оператора обобщённой инверсии Iv, выполняются все нужные свойства коммутативности, ассоциативности, нейтрального и противоположного элемента:
Коммутативность: х +*у = Iv (Iv (x) + Iv (y)) = Iv (Iv (у) + Iv (х)) =
= у +*х,
Ассоциативность: ((х +*у) +*z) = Iv (Iv (Iv (Iv (x) + Iv (y))) + Iv (z)) =
= Iv ((Iv (x) + Iv (y)) + Iv (z)) = Iv (Iv (x) + (Iv (y) + Iv (z))) =
= Iv (Iv (x) + Iv (Iv (Iv (y) + Iv (z))))) = (х +* (у +*z)),
Нейтральный элемент: х +*∞ = Iv (Iv (x) + Iv (∞)) = Iv (Iv (x) +0) =
= Iv (Iv (x)) = x,
Противоположный элемент: х +* (-х) = Iv (Iv (x + Iv (-x))) =
= Iv (Iv (x) — Iv (x)) = Iv (0) =∞.
Что же касается свойства дистрибутивности, то в общем случае для обычного умножения и операции обратного сложения +*, определённого через оператор обобщённой инверсии, оно уже не выполняется. Но если мы введём операцию обратного умножения
х ⋅ *у = Iv (Iv (x) ⋅ Iv (y)),
то для этой операции сможем получить дистрибутивность:
Дистрибутивность: z ⋅* (x+*y) = Iv (Iv (z) ⋅ Iv (Iv (Iv (x) + Iv (y)))) =
= Iv (Iv (z) ⋅ (Iv (x) + Iv (y))) = Iv (Iv (z) Iv (x) + Iv (z) Iv (y)) =
= Iv (Iv (Iv (Iv (z) Iv (x))) + Iv (Iv (Iv (z) Iv (y)))) = Iv (Iv (z ⋅ *x) +
+ Iv (z ⋅* y)) = (z ⋅* x) +* (z ⋅* y).
Только для случая Iv (x) = Inv (x) = x-1 получаем совпадение обратного умножения с обычным умножением:
х ⋅* у = Inv (Inv (x) ⋅ Inv (y)) = (x-1 ⋅ y-1) -1 = xy.
Аналогично для операции обратного умножения могут быть доказаны все групповые свойства (достаточно в приведённых выше доказательствах для обратного сложения заменить + на ⋅):
Коммутативность: х ⋅* у = Iv (Iv (x) ⋅ Iv (y)) = Iv (Iv (у) ⋅ Iv (х)) =
= у ⋅* х,
Ассоциативность: ((х ⋅* у) ⋅* z) = Iv (Iv (Iv (Iv (x) ⋅ Iv (y))) ⋅ Iv (z)) =
= Iv ((Iv (x) ⋅ Iv (y)) ⋅ Iv (z)) = Iv (Iv (x) ⋅ (Iv (y) ⋅ Iv (z))) =
= Iv (Iv (x) ⋅ Iv (Iv (Iv (y) ⋅ Iv (z))))) = (х ⋅* (у ⋅* z)),
Нейтральный элемент: х ⋅*1* = Iv (Iv (x) ⋅ Iv (1*)) = Iv (Iv (x) ⋅ 1) =
= Iv (Iv (x)) = x,
Обратный элемент: х +* (х-1) * = Iv (Iv (x + Iv ((x-1) *)) =
= Iv (Iv (x) ⋅ Iv (x -1) = Iv (1) = 1*,
где в качестве нейтрального элемента 1* выбран такой, что
Iv (1*) = 1,
и в качестве обратного элемента x-* такой элемент, что выполнено соотношение:
Iv (x-*) = Iv (x) -1.
Также можем определить обратный порядок по правилу:
х <* у е. т. е. Iv (x) <Iv (y).
Если теперь под множеством IvR понимать множество вещественных чисел, на которых определены операции обратного сложения и умножения, используя оператор обобщённой инверсии, то мы получаем структуру на IvR как поле с описанными выше определениями.
Таким образом, мы не только вскрываем R-корни обычных операций умножения и деления, но и обобщаем эти операции до случаев обратного сложения и умножения.
12. Обратная топология
Подобно тому как на 0-числах может быть задана стандартная (прямая) топология, где базовым открытым множеством является интервал вида (a,b) при a <b, подобно этому на множестве обратных чисел х∞ может быть задана своя топология, наиболее характерная для данного типа чисел. Эту топологию можно называть обратной топологией.
Различие этих топологий уходит своими корнями в различие двух количественных полюсов — полюса нуля и бесконечности. Если с точки зрения аддитивной метрики (метрики сложения и вычитания) ноль является соизмеримой величиной для любых конечных чисел, т.е. между нулём и конечным числом конечное расстояние, то между конечными числами и бесконечностью лежит бесконечно большое расстояние. Это делает полюс бесконечности несоизмеримым с конечными величинами.
К чему приводит такое различие с топологической точки зрения?
Для разных 0-чисел всегда можно найти такие окрестности, которые не пересекаются между собой. В конечном итоге это свойство уходит в пределе в существование бесконечно малых монад вокруг каждого 0-числа х0. 0-Число как центр своей монады подобно в этом случае нулю со своей монадой. Тем самым ненулевое число может быть представлено как ноль в своей системе отсчёта. Все ненулевые числа как бы вышли из нуля и затем разошлись по своим местам, но сохранили роль относительного нуля как память о своем тождестве с нулём. Операционально это можно выразить введением бичисел вида ух — величины у, отсчитываемой от х как нуля. Здесь можно ввести эквивалентность вида
ух ≈ (у+х) 0,
где у0 — в данном случае величина у, отсчитываемая от нуля. В системе бичисел ух величина х выступает относительным нулём, выражая тем самым своё родство с абсолютным нулём 0. Это можно рассматривать как размножение природы нуля на все вещественные числа, что и означает «выход всех чисел из нуля». В этом аспекте все числа подобны нулю. Но система у0 абсолютного нуля 0 является всё же господствующей, и она позволяет отличить ноль от всех иных чисел. Операциональным выражением такого отличия является также топологическая отделимость ненулевых чисел от нуля.
Иными словами, в случае 0-чисел мы можем перенести количественный полюс в любое конечное число, отделив монаду этого числа от монады нуля. Тем самым для любых неравных 0-чисел обеспечивается свойство отделимости, т.е. возможность найти для них непересекающиеся окрестности, вплоть до монад — как бесконечно малых окрестностей 0-чисел. Условием такого свойства является конечная соизмеримость полюса нуля и конечных чисел: ноль лежит на конечном расстоянии от конечных чисел, и от него можно отделиться, выведя окрестность конечного числа за границы нуля.
Иное дело — полюс бесконечности. Он лежит на бесконечно большом расстоянии от конечных чисел, и в рамках таких отношений его невозможно достичь. А значит, если здесь также все числа исходно совпадали с бесконечностью и лишь затем стали расходиться, так что края окрестности лежали по разные стороны от бесконечности, то такую окрестность конечного числа нельзя вывести за границы бесконечности, сдвигая число от бесконечности в конечную область, и тем самым невозможно обеспечить отделимость ∞-чисел. В этом случае ∞-числа оказываются неотделимыми друг от друга, и они не могут взять на себя роль количественного полюса, равноправного полюсу бесконечности, — они все оказываются привязанными к полюсу бесконечности. Подобную неотделимость ∞-чисел можно рассматривать как одно из средств обеспечения их когерентности — когда они все проникают друг в друга, являясь разными аспектами одного.
Тем самым предполагается важное различие 0- и ∞-чисел: если 0-числа отделимы друг от друга, конечно соизмеримы со своим количественным полюсом, и каждое из них может стать относительным нулём; то ∞-числа иные — они все неотделимы друг от друга, несоизмеримы со своим количественным полюсом и не могут взять на себя его роль, будучи определёнными только в его системе х∞.
Такова основная идея, которая добавляет новые аспекты в понимании прямого и обратного количества. Теперь остаётся воплотить её более строго.
Предполагая, что на 0-числах задана стандартная топология с открытыми интервалами как базовыми открытыми множествами, зададим топологию на ∞-числах, отталкиваясь от понятия базовых ∞-окрестностей.
Рассмотрим множество ∞-величин х∞, где есть элемент ∞∞, и нет элемента 0∞. Ведём на этом множестве открытые множества следующего вида
О∞ (z1,z2) = {y∞: z1 <0 ∧ z2> 0 ∧ (y <z1 ∨ y> z2 ∨ y = ∞)}.
Это интервалы с границами z1 <0, z2> 0 и включающие в себя элемент ∞∞.
Для объединения и пересечения этих множеств имеем:
О∞ (z1,z2) ∪ О∞ (z1», z2») = О∞ (max {z1,z1»},min {z2,z2»}),
О∞ (z1,z2) ∩ О∞ (z1», z2») = О∞ (min {z1,z1»},max {z2,z2»}).
Можно показать, что это в самом деле открытые множества, поскольку любое объединение их есть открытое множество, и только конечное пересечение есть открытое множество, поскольку при бесконечном пересечении мы можем получить множество {∞∞}, которое есть замкнутое множество.
Тогда получаем определённую топологию на множестве ∞-чисел, которую можно называть обратной топологией.
Как обычно, в качестве окрестности О∞ (х∞) числа х∞ назовём такое открытое множество О∞ (z1,z2), которое включает в себя х∞.
В этой топологии любые два числа х∞ и у∞ неотделимы, т.е. не существует их ∞-окрестностей, которые не пересекаются между собой, поскольку все они окружают точку ∞∞, поэтому и их пересечение будет также включать в себя эту точку, т.е. не будет пустым множеством.
Обратная топология требует, чтобы мы не смогли сдвинуть край окрестности за точку ∞∞, т.е. чтобы точка ∞∞ была бесконечной. Точка ∞∞ станет конечной, когда мы перевернём топологию, т.е. от х∞ перейдём к Iv (x) 0 — встанем на точку зрения бесконечности как нуля.
Как уже отмечалось, в обычной (прямой) топологии на множестве R отделимость двух неравных точек означает в конечном итоге их принадлежность двум разным монадам. Если в обратной топологии любые две точки неотделимы между собой, то можно предполагать, что они все принадлежат одной монаде — монаде ∞∞, и эту монаду можно называть обратной монадой. Это всё множество ∞-чисел.
Также, когда мы сдвигаем 0-окрестность, выводя её из нуля, то в пределе это выражается в образовании своей монады для ненулевой точки, которая изнутри себя выглядит как монада нуля, т.е. это выражает возможность образования величин уx, когда х становится новым количественным полюсом. Для ∞-величин это невозможно — они все центрированы относительно только одного полюса бесконечности, что делает их однополюсными.
Итак, теперь мы более строго можем обеспечить когерентность обратных величин, используя более простые средства, чем квантовые структуры, но в то же время сохраняя в будущем возможность скоординировать эти более простые средства и с квантовыми структурами. Таким более простым средством выступает обратная топология.
Если на прямых величинах органично задаётся прямая (стандартная) топология с отделимостью всех разных величин, то на обратных величинах столь же органично задаётся обратная топология с неотделимостью в том числе разных обратных величин.
Здесь только нужно иметь в виду, что в общем случае в структурах R-анализа взаимодействуют финитные и инфинитные позиции R-структур, и в разных случаях их пропорция может быть разной, обеспечивая ослабление или усиление той или иной скоординированной с данной пропорцией R-структуры.
Например, обратная топология предполагает не только инфинитную, но и элементы финитной позиции полюса бесконечности (например, в рядополагании элемента ∞∞ и элементов х∞), но инфинитная позиция здесь преобладает, чтобы обеспечить несоизмеримость полюса бесконечности и конечных величин при невозможности выйти краю ∞-окрестности за точку бесконечности и тем самым исключить элемент ∞∞ из состава этой окрестности.
13. Решение задачи симметрии бесконечно большого и бесконечно малого
Напоминаю, что проделанная выше работа с идеями прямого и обратного количества имела целью дать более точную интерпретацию троек (р,х,у). В первую очередь пока не ясна реализация бесконечно большой величины р. В связи с чем мы должны будем вновь обратиться к теме бесконечно большого.
Первое, что нужно заметить, что бесконечно большое лежит не только в области плюс бесконечности +∞, но и минус бесконечности -∞. Если мы предполагаем, что это проекция на шкалу конечных величин самостоятельной количественной системы, которая изнутри себя имеет ту же структуру вещественных чисел, то получается, что эта система разорвана в области своего нуля, и положительная её половина попадает в область +∞, а отрицательная половина — в область -∞. Также мы видим, что бесконечно большое ∞ = 1/ (1/∞) мультипликативно перевёрнуто относительно бесконечно малого, т.е. здесь определено отношение мультипликативной инверсии.
Всё это позволяет предоположить, что бесконечно большие величины при симметричной интерпретации тройки (у,х,р) находятся в отношении мультипликативной, а в более общем случае — обобщённой инверсии в отношении к конечным и бесконечно малым величинам. Тогда становится понятен и феномен разрыва нуля, поскольку ноль оказывается недостижимой величиной для обратных величин, а их своеобразным нулём является точка ±∞.
Теперь мы можем уточнить, что р* — это не просто величина Inv (p), но Iv (p), где используется оператор обобщённой инверсии. То же верно и для х*. Также когда мы используем операцию +*, то должны понимать её как обратное сложение через оператор обобщённой инверсии, т.е. везде мы переходим на более универсальную позицию не просто мультипликативной, но обобщённой инверсии для бесконечно больших величин.
При использовании такой интерпретации бесконечно большая величина р выражает собственную метрику обратной величины, которую мы представляли формой ∞р. Что же касается конечной величины х, то в операциях с бесконечно малыми и 0-конечными величинами она дана как 0-количество х0, когда же она фигурирует в операциях с обратным количеством, то дана как величина х*∞ = Iv (х) ∞, собственная обратная метрика которой есть ∞x. Так теперь выглядит более точная интерпретация тройки (р,х,у).
Но вернёмся к теме симметрии бесконечных координат относительно конечной координаты.
Начнём с пары (х,у) конечного количества х и бесконечно малой величины у. Её интерпретация такова:
(х,у) = x + dy,
что в случае (-1) -реализации будет выглядеть как сумма
r-1 (x,y) = x + R-1m (y)
монадического приращения R-1m (y) и конечной величины х как центра монады (х-m,x+m).
Далее рассмотрим пару (р,х) из конечного х и бесконечно большого р количества. Её интерпертация имеет вид:
(р,х) = ip + x.
Кроме того, примем во внимание, что бесконечно большая величина р дана при своей реализации как обратное количество, и как такое же обратное количество дана величина х. Это значит, что есть две количественные системы обратного количества — конечная и бесконечно большая, и первая проецируется во вторую. Причём, пока мы их рассматриваем изнутри них самих — как прямые количества в своих внутренних определениях.
Итак, мультипликативная инверсия дифференциала d и интеграла i в операциях на поличислах, т.е. i = d-1, является символом принадлежности соответствующих величин системам прямого и обратного количества, и одновременно бесконечно большие величины сохраняют тот же порядок в отношении к конечным величинам, что и конечное к бесконечно малому, — этот порядок не переворачивается, но остаётся сквозным для всех систем. Отсюда мы и получаем симметричную реализацию как иерархически обратную, т.е. ту же иерархию систем, но с обратными величинами.
Если бесконечно большие величины мы начнём интерпретировать как обратные величины в бесконечно малых системах, мы потеряем смысл бесконечно большого как иерархически большего количества в отношении к конечному количеству.
Если мы будем использовать прямые величины бесконечно больших, сохраняя иерархию, мы откажемся от инверсии дифференциала и интеграла.
Мы не можем непосредственно использовать прямую R-функцию для выражения интеграла i, определяя прямую R-функцию на всём множестве конечных чисел (поскольку область определения прямой R-функции не распространяется на всё множество вещественных чисел), поэтому мы вынуждены, сохраняя иерархию конечного и бесконечно большого, сначала перейти в систему бесконечно большого, чтобы оттуда выразить отношение бесконечно большого и конечного, т.е. выразить интеграл конечного через внутреннее количество бесконечно большого, что приводит к представлению конечного через дифференциал (обратную R-функцию) в этой системе.
И здесь, как это было описано выше, конечное количество проецируется некоторой обратной базовой R-функцией R-1М в область бесконечно большого количества, образуя интервал (-М,М). Так что в целом получаем величину
р + R-1М (х).
Но мы должны понимать, что это величина в собственной метрике бесконечно большой количественной системы обратного количества. И если мы хотим спроецировать эту величину на шкалу прямого количества той же бесконечно большой системы, то мы должны будем применить к обратной величине оператор обобщённой инверсии, т.е. в конечном итоге получим такую интерпретацию пары (р,х) из тройки (р,х,у):
Iv (р + R-1М (х)) = Iv (p) +*IvoR-1M (x) = p* +*IvoR-1M (x),
где Iv = R+1M’oDM’oR-1M»,
и R-1M» не обязательно совпадает с R-1M, а операция +* также определена через Iv.
Сделаем ещё один шаг — представим Iv (R-1M (х)) как действие некоторой функции IR-1M на х* = Iv (х), т.е.
Iv (R-1M (х)) = IR-1M (х*).
Найдём выражение для функции IR-1M. Имеем:
Iv (R-1M (х)) = Iv (R-1M (Iv-1 (Iv (х))) = Iv (R-1M (Iv-1 (p*)) = IR-1M (p*),
откуда получаем:
IR-1M = IvoR-1MoIv-1.
Итак, для выбранной нами новой реализации пары (р,х) получаем следующее выражение:
r* (р,х) = р* +* IR-1M (х*).
Учитывая новую реализацию для бесконечно больших, запишем теперь новую, более точную симметричную версию реализации тройки:
r±1 (p,x,y) = (р* +*IR-1M (х*), R-1М (х + R-1m (y))),
т.е. это пара двух реализаций бесконечных количеств, ведущих себя симметрично относительно центрального конечного количества. Симметрия в данном случае обеспечивается оператором обобщённой инверсии Iv (см. рис. 9).
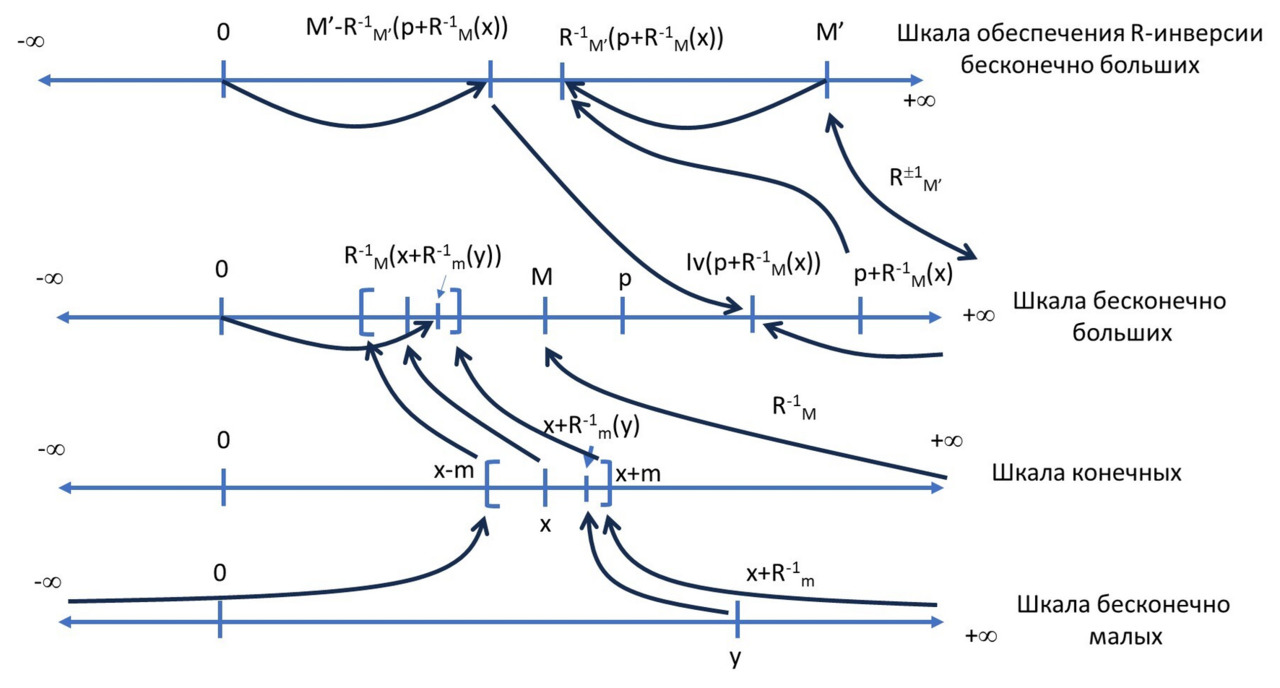
(стрелка справа).
Все эти новые интерпретации и реализации для тройки не сказываются на алгебре троек, но необходимы для более глубокого понимания их смысла. Симметричные тройки (р,х,у) описывают как бы трёхслойное количество — единство бесконечно малого, конечного и бесконечно большого количеств, но ведущих себя не так, как это принято в современной математике, а симметрично (в смысле оператора Iv) относительно конечного количества.
Тем самым мы завершаем небольшое индуктивное введение в R-анализ, останавливаясь на конструкциях трёхслойного количества, выраженного тройками (р,х,у) и их симметричными интерпретациями.
В итоге мы видим постепенно обретающие своё проявление контуры некоторой математической техники, которая начинает явно работать не только с количеством, но и с его качеством, что позволяет отслеживать разные количественные системы. Далее вводятся R-функции, которые способны очерчивать границы количественных систем, причём, что особенно важно, — финитизировать эти границы, если в некоторой перспективе они даны бесконечно. Это позволяет по-новому выразить отношение: вначале конечного и бесконечно большого количества, затем — конечного и бесконечно малого, и, наконец, соединить в более сложной конструкции все эти три вида количества. В итоге мы получаем некоторый стартовый аппарат, в котором, отражаясь как в капле воды, в миниатюре уже могут быть представлены все основные конструкции R-анализа.
В такой манере своего рода 3R-анализа — версии R-анализа, работающего с тройками (р,х,у), — можно и далее иллюстрировать многие его идеи, но на них постоянно будет лежать отпечаток сужения только до своего частного случая. Поэтому далее мы расширим перспективу, и, отталкиваясь от первых структур 3R-анализа, выйдем на первое обобщение работы с таким многослойным количеством, где будут представлены бесконечные (бесконечно малые и бесконечно большие) n порядков.
Это позволит нам ввести более универсальные структуры R-анализа и держаться более широкой точки зрения, хотя конечно и она может далее всё более расширяться, что неизбежно в любом познании истины.
В итоге далее я изменю свой стиль изложения и перейду к более дедуктивному представлению идей R-анализа, предполагая, что читатель получил некоторые интуиции R-анализа от первоначального более индуктивного введения, которое постепенно привело нас к конструкциям 3R-анализа. Теперь необходимо их обобщить.
Глава 2. К элементам дедуктивного построения
R-анализа
1. n-Предполе поличисел nF
Выше мы подошли к конструкциям R-анализа, используя тройки (р,х,у), где р — бесконечно большое количество, х — конечное и у — бесконечно малое количество. Алгебра на тройках определялась на основе первичной интерпретации вида
(*) (р,х,у) = ip + x + dy.
Хотя в дальнейшем интерпретация троек была усложнена, чтобы выразить симметрию бесконечно большого и малого количества, но для задания алгебры на тройках интерпретации (*) было достаточно. Идею такой интерпретации и связанной с нею алгебры можно обобщить на большее число координат, приходя к более общему виду последовательностей чисел
α = {xi} ni=-n = (x-n,x-n+1,…,x-1,x0,x1,…,xn-1,xn),
где n=0,1,…, и для любого i число xi является вещественным числом.
Договоримся, что бесконечно малые количества идут с отрицательными индексами, а бесконечно большие — с положительными. Конечное количество выражается числом х0 с нулевым индексом. Модуль индекса выражает порядок бесконечности той количественной системы, которой принадлежит данное число. Например, х-3 — это выражение бесконечно малого количества третьего порядка, х5 — бесконечно большого количества пятого порядка и т. д.
При задании алгебры будем, как и ранее, для последовательности α = {xi} ni=-n использовать интерпретации вида
∑ni=-n iixi,
где iixi = d-ixi при i <0.
В итоге будет получена некоторая структура, обобщающая алгебру троек. Ниже эта структура будет описана более строго.
Итак, рассматриваем последовательности вида
α = {xi} ni=-n = (x-n,x-n+1,…,x-1,x0,x1,…,xn-1,xn),
где n = 0,1,…, и для любого i число xi есть вещественное число.
Назовём последовательности α = {xi} ni=-n поличислами.
Пусть (α) i = αi = xi — i-я координата поличисла α.
Сложение и вычитание определяем покоординатно, где
— α = — {xi} ni=-n = {-xi} ni=-n.
Для умножения примем правило:
Если α = {xi} ni=-n, β = {уi} ni=-n, то
α∙β = {zi} ni=-n,
где zi = ∑k+m=ixkym.
Например, для n=1 получим:
(х-1,х0,х1) ∙ (у-1,у0,у1) = (х-1у0+у-1х0, х-1у1+х0у0+х1у-1, х0у1+у0х1).
В качестве нейтрального элемента умножения выступает элемент
n1 = {ei} ni=-n,
где e0=1, ei=0 при i≠0.
В самом деле, здесь получим:
α ∙ n1 = {xi} ni=-n ∙ {ei} ni=-n = {yi} ni=-n,
где yi = ∑k+m=ixkem = xie0 = xi.
Определим далее обратный элемент α-1 = {уi} ni=-n по правилу:
α ∙ α-1 = n1, т.е.
{xi} ni=-n ∙ {уi} ni=-n = {ei} ni=-n, откуда имеем
∑k+m=ixkym = ei, т.е.
∑k+m=ixkym = 0 при i≠0,
∑k+m=ixkym = 1 при i=0.
Например, для n=1 получим:
α = (х-1,х0,х1),
α-1 = (у-1,у0,у1),
11 = (0,1,0),
α ∙ α-1 = (х-1,х0,х1) ∙ (у-1,у0,у1) =
= (х-1у0+у-1х0,х-1у1+х0у0+х1у-1,х0у1+у0х1) = (0,1,0),
т.е. для трёх неизвестных у-1, у0 и у1 имеем три уравнения:
х-1у0+у-1х0 = 0,
х-1у1+х0у0+х1у-1 = 1,
х0у1+у0х1 = 0.
Решая их, получим следующие случаи (подробнее структуру решения см. в Приложении 2):
I. Случаи, когда обратный элемент для тройки (х-1,х0,х1) определён:
1.1.1. х-1≠0, и (х-1,0,0) -1 = (у-1,0,1/х-1),
где у-1 может быть любым вещественным числом,
1.2.1. х1≠0, и (0,0,х1) -1 = (1/х1,0,у1),
где у1 может быть любым вещественным числом,
1.2.2.1—2. при х-1≠0, х0=0 и х1≠0 и х-1у1 + х1у-1 = 1
имеем (х-1,0,х1) -1 = ((1-х-1у1) /х1, 0, (1-х1у-1) /х-1),
2.1. при х0≠0, х02 — 2х1х-1 ≠ 0 имеем:
(х-1,х0,х1) -1 = (-х-1/ (х02 — 2х1х-1), х0 / (х02 — 2х1х-1), -х1 /
/ (х02 — 2х1х-1))
II. Случаи, когда обратный элемент для тройки (х-1,х0,х1) не определён:
1.1.2. тройка (0,0,0),
1.2.2.3. тройка (х-1,0,х1), где х-1≠0 и х1≠0,
2.2. тройка (х-1,х0,х1), где х0≠0 и х02 — 2х1х-1 = 0.
Таким образом, не все ненулевые элементы имеют обратный, т.е. мы имеем дело не с полем.
Будем называть эту структуру n-предполем и обозначать nF.
Порядок на элементах n-предполя определим таким образом:
α <β е. т. е. (αn <βn) ∨∃m∀k> m (αk=βk∧αm <βm).
Для любых элементов α, β и γ из nF верно, что
(α + β) ⋅ γ = (α ⋅ γ) + (β ⋅ γ) и γ ⋅ (α + β) = (γ ⋅ α) + (γ ⋅ β).
В самом деле, если α = {αi} ni=-n, β = {βi} ni=-n, γ = {γi} ni=-n, то
((α + β) ⋅ γ) i = ∑k+m=i ((αk + βk) ⋅ γm) = ∑k+m=i (αkγm + βkγm) =
= ∑k+m=iαkγm + ∑k+m=iβkγm = (α ⋅ γ) i + (β ⋅ γ) i = ((α ⋅ γ) +
+ (β ⋅ γ) i.
Отсюда получаем правую дистрибутивность. Аналогично доказывается свойство левой дистрибутивности.
Введём для двух поличисел α и β область равенства (Е-область, Е-отрезок) как отрезок [m,n], где m≤n, индексов всех тех элементов от m до n, которые равны у α и β, а элементы αm-1 и βm-1 впервые не равны. Если α <β, то, согласно определению (αn <βn) ∨∃m∀k> m (αk=βk∧αm <βm), отрезок [m+1,n] не пустой (как минимум, он имеет вид [n,n]). И наоборот, если Е-отрезок [m,n] не пустой, то порядок на αm-1 и βm-1 определяет порядок на α и β.
Покажем, что отношение α <β является строгим порядком:
1. Нерефлексивность: ¬ (α <α).
Предположим противное: что найдётся такое α, где α <α, т.е. (αn <αn) ∨∃m∀k> m (αk=βk∧αm <αm), но тогда либо (αn <αn), либо для некоторого αm имеем αm <αm, что в любом случае неверно.
2. Несимметричность: если α <β, то не верно, что β <α.
Пусть α <β. Тогда (αn <βn) ∨∃m∀k> m (αk=βk∧αm <βm). Если (αn <βn), то не верно, что βn <αn, что уже исключает случай β <α. Если же ∃m∀k> m (αk=βk∧αm <βm), то найдётся Е-отрезок [m+1,n], где αm <βm. Но тогда, если бы β <α, то у α и β был бы тот же Е-отрезок [m+1,n], где было бы βm <αm, что не верно.
3. Транзитивность: если α <β и β <γ, то α <γ.
Пусть α <β и ∃m∀k> m (αk=βk∧αm <βm). Пусть также β <γ и ∃m’∀k> m’ (βk=γk∧βm’ <γm’). Тогда для α и β имеем Е-отрезок [m+1,n], а для β и γ Е-отрезок [m’+1,n]. Пусть m≤m’. Тогда γm’> βm’=αm’, т.е. γm’> αm’. Следовательно, для α и γ существует непустой Е-отрезок [m’+1,n], где αm’ <γm’, т.е. α <γ. Пусть, с другой стороны, m> m’. Тогда αm <βm=γm, т.е. для α и γ определён Е-отрезок [m,n], где αm <γm, т.е. α <γ. Остальные случаи рассматриваются аналогично.
Равенство на поличислах α=β определяем покоординатно, и нестрогий порядок α≤β определяем обычным образом:
α≤β е. т. е. α <β или α=β.
Далее покажем, что порядок на поличислах является линейным, т.е. выполнено требование трихотомии:
Для любых двух поличисел α, β верно: либо α <β, либо β <α, либо α=β.
Если даны два неравных поличисла α и β, то у них либо уже n-е элементы не равны, либо для них определён ненулевой Е-отрезок [m+1,n]. В любом случае для α и β найдутся первые неравные координаты с одним индексом, обозначим их αm и βm. Поскольку αm и βm — вещественные числа, то для них выполнена аксиома трихотомии, т.е. либо αm <βm, либо βm <αm, что и определяет трихотомию для α и β.
Сложение на поличислах из nF образует абелеву группу, что очевидно, в силу покоординатного определения сложения и противоположного элемента. В качестве нейтрального элемента сложения выступает элемент n0, у которого все координаты нулевые.
Покажем, что умножение на поличислах комутативно и ассоциативно.
Для αβ имеем (αβ) i = ∑k+m=iαkβm = ∑k+m=iβmαk = (βα) i,
т.е. αβ = βα.
Далее, ((αβ) γ) i = ∑p+s=i (∑k+m=pαkβm) γs = ∑k+m+s=iαkβmγs =
= ∑k+ (m+s) =iαk (∑m+s= (i-k) βmγs) = (α (βγ)) i, т.е. (αβ) γ = α (βγ).
Наконец, покажем дистрибутивность:
(α (β+γ)) i = ∑k+m=iαk (βm+γm) = ∑k+m=iαkβm + ∑k+m=iαkγm = (αβ) i + (αγ) i = (αβ + αγ) i. Это означает, что α (β+γ) = αβ + αγ, т.е. левую дистрибутивность. Правая дистрибутивность доказывается аналогично.
В итоге мы получаем математическую структуру, n-предполе nF, на которой определены абелевы группы по сложению и умножению, операции сложения и умножения связаны через правую и левую дистрибутивность, а также задан порядок, для которого выполнена аксиома трихотомии. В то же время, в силу наличия делителей нуля, такая структура не является полем.
n-Предполе nF — это одна из центральных структур R-анализа, хотя, как будет видно далее, далеко не единственная сфера его определения и развёртывания, но она создаёт как бы некоторую ядерную конструкцию, относительно которой строятся все последующие структуры R-анализа.
Поличисло α = {xi} ni=-n представляет многослойное количество, т.е. количество, включающее в себя более частные количества разных слоёв — разных количественных систем. Здесь есть центральное конечное количество х0, относительно которого определяются производные количества бесконечно малых x-m и больших xm разных порядков, вплоть до n-го порядка. Пока мы можем складывать и умножать такие поличисла, определять порядок на них. Хотелось бы теперь попытаться определить на них те или иные функции. Ряд построений будет далее посвящён именно этой теме.
В решении задачи определения функций на поличислах должно сыграть определённую роль некоторое обобщение ряда Тейлора. В самом деле, когда в стандартном анализе мы определяем ряд Тейлора для аналитической функции f, т.е. пишем разложение вида
f (x + Δx) = ∑∞k=0 (f (k) (x) /k!) Δxk,
где f (k) (x) — k-я производная функции f (x),
то это можно проинтерпретировать как задание ряда Тейлора для пары (х, Δх), где х представляет конечное количество, а Δх — бесконечно малое количество первого порядка, т.е. ряд Тейлора по сути задаётся для двуслойного количества, определяя функцию только для двуслойного аргумента. Но теперь перед нами задача обобщить подобное преобразование до поличисел. Следовательно, могло бы быть и некоторое обобщение ряда Тейлора, которое бы позволило нам определять функции для поличисел.
Эта тема и будет исследоваться далее.
2. Ряд Тейлора для суммы приращений
Задача теперь состоит в том, чтобы определить функции на поличислах. И это определение должно быть согласовано с алгеброй на поличислах. Операции сложения и умножения на поличислах — это также некоторые функции на них, и общее определение функций на поличислах должно включать в себя как частный случай и эти операции.
В итоге план таков: 1) определить степенные функции для поличисел, 2) если общее определение степенных функций будет связано с рядом Тейлора, то через него можно определить другие функции.
Но таким путём мы сможем определить функции только для конечной и бесконечно малых координат поличисла (для которых и определяется ряд Тейлора). Что же касается бесконечно больших координат, то здесь можно использовать описанную выше Iv-симметрию, т.е. определяя функции для бесконечно больших координат так же, как для бесконечно малых, но понимая их в смысле внутреннего представления обратной метрики бесконечно больших величин.
Тогда первый шаг состоит в выведении общей формулы для суммы приращений разных порядков в ряде Тейлора:
f (x + ∑mi=1Δiyi).
Пусть Δх = ∑mi=1Δiyi. Тогда имеем:
f (x + Δx) = ∑∞k=0 (f (k) (x) /k!) Δxk,
где Δxk = (∑mi=1Δiyi) k.
Например,
(Δу1 + Δ2у2) 2 = (Δу1 + Δ2у2) (Δу1 + Δ2у2) = Δу12 +2Δу1Δ2у2 + Δ4у22,
(Δу1 + Δ2у2) n = ∑nk=0 (n!/k! (n-k)!) (Δу1) n-k (Δ2у2) k.
Существует общая формула полинома Ньютона:
(x1 + x2 + … +xm) n = ∑kj≥0,k1+k2+...+km=n(n!/k1!k2!...km!) x1k1x2k2…xmkm.
Пусть Δiyi = yi. Тогда
(Р) ⠀ Δxp = (∑mi=1Δiyi) p = (∑mi=1yi) p =
= ∑kj≥0,k1+k2+...+km=p(p!/k1!k2!...km!) y1k1y2k2…ymkm.
В нашем случае нужны члены только до р=n. Также m=n.
3. Первые совпадения
Посмотрим на поличисло вида (х-3,х-2,х-1,х0,0,0,0). Найдём его степени сначала алгебраически:
(х-3,х-2,х-1,х0,0,0,0) 2 =
= (2х0х-3+2х-1х-2,2х0х-2+х-12,2х0х-1,х02,0,0,0).
Теперь найдём из ряда Тейлора.
δx = Δх + Δ2у + Δ3z,
f (x) = x2,
f (x + δx) = f (x) + f (x)«δx = x02 +2x0 (Δх + Δ2у + Δ3z) =
= x02 +2x0Δх +2x0Δ2у +2x0Δ3z,
f (x + δx) = f (x) + f (x)«δx +0.5f (x)»«δx2 = x02 +2x0 (Δх + Δ2у + Δ3z) +
+ δx2 = x02 +2x0Δх +2x0Δ2у +2x0Δ3z + (Δх + Δ2у + Δ3z) 2 =
= 3x02 +2x0Δх +2x0Δ2у +2x0Δ3z + Δх2 +2ΔхΔ2у =
= x02 +2x0Δх + (Δх2 +2x0Δ2у) + (2x0Δ3z+2ΔхΔ2у),
где =3 — равенство с учётом только приращений не больше третьей степени.
Случай
f (x + δx) = f (x) + f (x)«δx +0.5f (x)»«δx2 + (f (x)»'»/6) δx3
уже нет смысла рассматривать, т.к. f (x)»'» = 0 для х2.
Таким образом, вновь имеем совпадение с рядом Тейлора, даже когда степень n в хn меньше числа р бесконечно малых координат (в данном примере 3). Но ряд Тейлора нужно искать именно для малых порядка р.
Подпадают ли выражения для ряда Тейлора под выведенную выше формулу (Р)?
Для случая δx = Δх + Δ2у + Δ3z по формуле (Р) имеем (если принять, что у1 = Δх, у2 = Δ2у, у3 = Δ3z):
(∑3i=1yi) 1 = ∑kj≥0,k1+k2+k3=1 (1!/k1!k2!k3!) y1k1y2k2y3k3 = y1+y2+y3,
(∑3i=1yi) 2 = ∑kj≥0,k1+k2+k3=2 (2!/k1!k2!k3!) y1k1y2k2y3k3 = y12 + y22 +
+ y32 +2y1y2 +2y1y3 +2y2y3.
Если принять у1 = х-1, у2 = х-2, у3 = х-3, то имеем:
(∑3i=1yi) 2 = х-12 + х-22 + х-32 +2х-1х-2 +2х-1х-3 +2х-2х-3.
Мы видим, что для одного значения р мы получаем слагаемые разных степеней малости, из которых далее нужно отобрать только те, малость которых не превышает максимальной малости нашего поличисла. Здесь получим:
(∑3i=1х-i) 2 =-3 [∑kj≥0,k1+k2+k3=2 (2!/k1!k2!k3!) х-1k1х-2k2х-3k3] -3 =
= х-12 +2х-1х-2,
где =-р — равенство для малых порядка не больше р, [A] -p — результат ограничения выражения А до такого подвыражения А* выражения А, которое содержит только те элементы, малость которых не превышает р.
И вот какой важный момент: слагаемое ∑kj≥0,k1+k2+...+kn=k(k!/k1!k2!...kn!) x-1k1x-2k2…x-nkn может содержать произведения разных степеней малости, т.е. относящиеся к разным координатам поличисла. Поэтому это слагаемое нельзя писать в одной координате поличисла.
Но продолжим проверку:
f (x + δx) = f (x) + f (x)«δx +0.5f (x)»«δx2 = f (x) + f (x) ’ (х-1+х-2+х-3) +0.5f (x)»»(х-12 +2х-1х-2) = f (x) + f (x)«х-1+ f (x)«х-2+ f (x)«х-3 +0.5f (x)»«х-12 + f (x)»«х-1х-2 = f (x) + f (x)«х-1+ (f (x)«х-2+0.5f (x)»«х-12) + (f (x)«х-3 + f (x)»«х-1х-2).
При f (x) = x2 получаем:
(x + δx) 2 = x2 +2хх-1+ (2хх-2+ х-12) + (2хх-3 + +2х-1х-2),
что полностью соответствует алгебраическому выражению
(2х0х-3+2х-1х-2,2х0х-2+х-12,2х0х-1,х02,0,0,0).
Итак, подведём некоторый итог.
Если мы ищем степень р поличисла α, т.е. αр, где само поличисло имеет n бесконечно малых координат, а все бесконечно большие координаты нулевые, то мы можем использовать разложение степенной функции в ряд Тейлора до приращения малости р включительно и привлекать для общего выражения ряда формулы вида
f (x0 + Δx) = ∑pk=0 (f (k) (x0) /k!) Δxk,
Δx = ∑nm=1 (x-m),
Δxk = (∑nm=1 (x-m)) k = ∑kj≥0,k1+k2+...+kn=k(k!/k1!k2!...kn!) x-1k1x-2k2…x-nkn,
так что в целом для всего разложения в р-отрезок ряда Тейлора получим:
f (x0 + Δx) = ∑pk=0 (f (k) (x0) /k!) Δxk =
= f (x0) + ∑pk=1(f(k)(x0)/k!)∑kj≥0,k1+k2+...+kn=k(k!/k1!k2!...kn!) x-1k1x-2k2…x-nkn.
Но это выражение нельзя использовать для покоординатного представления получающегося в итоге поличисла.
Покоординатное представление имеет вид
[f (x0 + Δx)] -m = [∑pk=0 (f (k) (x0) /k!) Δxk] -m =
= [f(x0)+∑pk=1(f(k)(x0)/k!)∑kj≥0,k1+k2+...+kn=k(k!/k1!k2!...kn!) x-1k1x-2k2…x-nkn] -m.
где m = 0,1,…,р.
4. Общая формула для степенных функций на дифференциальных поличислах
Пусть <(k!/k1!k2!...kn!)> =k1+2k2+…+nkn — координата формы (k!/k1!k2!...kn!).
Для поличисла α = {xi} ni=-n введём его аддитивное представление (аддитивную форму)
sα = ∑ni=-nxi,
где xi понимается не просто как вещественное число, а как вещественное число с индексом i. Например, для тройки (2,7,5) из 1F получим
s (2,7,5) = 2—1 +70 +51.
В этом случае все основные свойства поличисел сохраняются, если в аддитивном представлении слагаемые группировать по индексам/координатам i. В частности, если дано слагаемое Пmj=-pxjkj, где m,p≥0, то под координатой <Пmj=-pxjkj> такого слагаемого следует понимать число ∑mj=-pjkj. Полное значение по данной координате будет суммой всех слагаемых с данной координатой.
С другой стороны, сумма вида А = ∑ri=-qПmiij=-pixijkij, где r,q≤n, может быть представлена как аддитивная форма некоторого поличисла, если его слагаемые сгруппировать покоординатно (брать суммы сумм, где у сумм первого порядка будут все слагаемые одной координаты). Тогда под s-1A = α можно понимать поличисло α, координаты которого равны координатам суммы А. Сумма вида А может называться координатной суммой.
Если дано поличисло β, где sβ = ∑-1i=-nxi, т.е. все координаты от нулевой и выше равны нулю, то его аддитивную форму можно рассматривать как сложное приращение.
Для этого сложного приращения мы можем записать верную формулу
(sβ) k = (∑-1i=-nxi) k = ∑k1+k2+...+kn=k,kj≥0(k!/k1!k2!...kn!) x-1k1x-2k2…x-nkn.
С другой стороны, имеем определение произведения поличисел
(αβ) i = ∑k+m=iαkβm.
Это определение верно для аддитивной формы поличисел. Если
sα = ∑nk=-nαk,
sβ = ∑nm=-nβm,
то для произведения имеем:

С другой стороны, рассматривая в поличисле α аддитивную форму как сумму х0 и приращения, можем записать следующее соотношение, используя разложение функции в ряд Тейлора:
f (sα) = f (∑0i=-nxi) = f (x0 + ∑-1i=-nxi) = ∑nk=0 (f (k) (x0) /k!) (∑-1i=-nxi) k =
= ∑nk=0(f(k)(x0)/k!)(∑k1+k2+...+kn=k,kj≥0(k!/k1!k2!...kn!) x-1k1x-2k2…x-nkn),
где f — функция класса гладкости Сn.
Для степенной функции можем записать:
(sα) p = (∑0i=-nxi) p = (x0 + ∑-1i=-nxi) p =
= ∑pk=0 ((p!/ (p-k)!) x0p-k/k!) (∑-1i=-nxi) k =
= ∑pk=0((p!/(p-k)!)x0p-k/k!)(∑k1+k2+...+kn=k,kj≥0(k!/k1!k2!...kn!) x-1k1x-2k2…x-nkn).
Теперь можно проверить, совпадают ли покоординатно суммы (sα) p, выраженные через полином Ньютона и через ряд Тейлора.
Проблема в том, что оба представления (sα) p не являются координатными суммами, и их прежде нужно так представить. А потом сравнить по координатам от i=0 до i=-n.
Во-первых, можно заметить, что
(sα) p = ∑pk=0((p!/(p-k)!)x0p-k/k!)(∑k1+k2+...+kn=k,kj≥0(k!/k1!k2!...kn!) x-1k1x-2k2…xnkn) = ∑pk=0(∑k1+k2+...+kn=k,kj≥0(p!/(p-k)!k1!k2!...kn!) x0p-kx-1k1x-2k2…x-nkn).
Во-вторых, представление через полином Ньютона нас интересует только до координаты -n, так что его можно представить в следующем виде:
(sα) p* = (∑0i=-nxi) p* = (p!/k0!k1!k2!...kn!) x0k0x-1k1x-2k2…x-nkn|k1+2k2+…+nkn=0,k0+k1+k2+…+kn=p, kj≥0 + ∑nm=1,k1+2k2+...+nkn=m,k0+k1+k2+...+kn=p,kj≥0(p!/k0!k1!k2!...kn!) x0k0x-1k1x-2k2…x-nkn =
(+) x0p + ∑nm=1,k1+2k2+...+nkn=m,k0+k1+k2+...+kn=p,kj≥0(p!/k0!k1!k2!...kn!) x0k0x-1k1x2k2…x-nkn, поскольку первое слагаемое обладает нулевой координатой, и k1+2k2+…+nkn=0 влечёт k1=k2=…=kn=0, что из условия k0+k1+k2+…+kn=p даёт k0=p.
В представлении через ряд Тейлора мы можем сделать аналогичные преобразования: (sα) p = ∑pk=0(∑k1+k2+...+kn=k,kj≥0(p!/(p-k)!k1!k2!...kn!) x0p-kx-1k1x-2k2…x-nkn) = (p!/(p-k)!k1!k2!...kn!) x0p-kx-1k1x-2k2…x-nkn) |k1+k2+…+kn=0,kj≥0 + ∑pk=1∑k1+k2+...+kn=k,kj≥0(p!/(p-k)!k1!k2!...kn!) x0p-kx-1k1x-2k2…x-nkn =-n x0p + ∑pk=1∑nm=1,k1+2k2+...+nkn=m,k1+k2+...+kn=k,kj≥0(p!/(p-k)!k1!k2!...kn!) x0p-kx-1k1x-2k2…x-nkn.
Обозначим k0 = p-k. Тогда k = p-k0, и варьирование k от 1 до р будет эквивалентно варьированию k0 от 0 до р-1, что как раз соответствует условию k0+k1+k2+…+kn=p для степеней х0 меньше р, так что последнее выражение можно представить в виде: (++) x0p + ∑nm=1,k1+2k2+...+nkn=m,k0+k1+k2+...+kn=p,kj≥0(p!/k0!k1!k2!...kn!) x0k0x-1k1x-2k2…x-nkn, что в точности (в рамках равенства = -n) соответствует последнему представлению (+) через полином Ньютона.
Таким образом, мы доказываем важную теорему:
Теорема 1. Если sα = ∑0i=-nxi, то
∀m=0, -1,…, -n ((s (α∙α∙ … ∙α)) m = (<Tp [f] (sα)> n) m),
где α∙α∙ … ∙α — произведение поличисла α на себя р раз, f (x) = xp, Tp [f] — ряд Тейлора от функции f до членов степени р.
Используя эту теорему, мы можем применять её и для поличисел α, где sα = ∑ni=0xi, используя оператор
Zα = β,
где βi = α-i.
Сначала переводим α в Zα, далее проводим с Zα нужные преобразования, получаем некое поличисло β, и в качестве нужного результата берём Zβ.
Tp [f] (sα) можно понимать как задание функции f на поличисле α, т. е. Tp [f] (sα) = sf (α). И эту идею теперь можно пытаться обобщить на другие функции, не только степенные.
5. Общая формула задания аналитических функций на поличислах
Пусть
α = {xi} ni=-n = (x-n,x-n+1,…,x-1,x0,x1,…,xn-1,xn), и
α = α- + α+,
где α- = (x-n,x-n+1,…,x-1,x0/2,0,…,0,),
α+ = {xi} ni=-n = (0,0,…,0,x0/2,x1,…,xn-1,xn).
Тогда
αn = (α-+α+) n = ∑nk=0 (n!/k! (n-k)!) (α-) n-k (α+) k.
Степени (α-) n-k и (α+) k мы можем определить на основе Теоремы 1. Следовательно, можем определить и αn.
Далее, если f — функция класса гладкости Сn, то мы для неё можем записать ряд Тейлора:
f (x+Δx) =-n ∑nk=0 (f (k) (x0) /k!) Δxk,
Также для поличисла α введём поличисло 0α, которое на нулевой координате имеет ту же координату, что α, а остальные координаты нулевые.
Пусть
— α = (x-n,x-n+1,…,x-1,0,0,…,0,),
+α = (0,0,…,0,0,x1,…,xn-1,xn),
n1 = (0,…,0,1,0,…,0).
Тогда
α = 0α + -α + +α.
Определим функцию f (α) на поличисле α∈nF в следующем виде:
(f) f (α) = f (0α + -α + +α) = f (0α + (-α + +α)) = ∑np=0 (f (p) (x0) /p!) (-α + +α) p = ∑np=0 (f (p) (x0) /p!) ∑pk=0 (p!/k! (p-k)!) (-α) p-k (+α) k.
Проверим эту формулу для α = (х-2,х-1,х0,х1,х2) и второй степени α2, где α2 = (2х-2х0 + х-12, 2х-2х1 +2х-1х0, х02 +2х-2х2 +2х-1х1, 2х-1х2 +2х0х1, 2х0х2 + х12).
Здесь имеем:
0α = (0,0,х0,0,0),
— α = (х-2,х-1,0,0,0),
+α = (0,0,0,х1,х2),
f (α) = α2 = (0α + (-α + +α)) 2 = ∑2p=0 (f (p) (x0) /p!) ∑pk=0 (p!/k! (p-k)!) (-α) p-k (+α) k = (f (0) (x0) /0!) ∑0k=0 (0!/k! (0-k)!) (-α) 0-k (+α) k + (f (1) (x0) /1!) ∑1k=0 (1!/k! (1-k)!) (-α) 1-k (+α) k + (f (2) (x0) /2!) ∑2k=0 (2!/k! (2-k)!) (-α) 2-k (+α) k = (x0) 2 (-α) 0 (+α) 0 +2х0 ((-α) + (+α)) + ((-α) 2 +2 (-α) (+α) + (+α) 2) = x02 (-α) 0 (+α) 0 +2х0 ((-α) + (+α)) + (-α) 2 +2 (-α) (+α) + (+α) 2,
(-α) 2 = (х-12,0,0,0,0),
(+α) 2 = (0,0,0,0,х12),
(-α) (+α) = (х-2,х-1,0,0,0) ∙ (0,0,0,х1,х2) = (x-2 + x-1) (x1 + x2) = x-2x1 + x-2x2 + x-1x1 + x-1x2 = (0,x-2x1,x-2x2 + x-1x1,x-1x2,0),
2x0 (-α) +2x0 (+α) + (-α) 2 +2 (-α) (+α) + (+α) 2 = (2x0х-2,2x0х-1,0,0,0) + (0,0,0,2x0х1,2x0х2) + (х-12,0,0,0,0) + (0,2x-2x1,2x-2x2 +2x-1x1,2x-1x2,0) + (0,0,0,0,х12) = (2x0x-2 + x-12, 2x0х-1+2x-2x1, 2x-2x2 +2x-1x1, 2x0х1+2x-1x2, 2x0х2+ х12).
Примем, что
α0 = n1, тогда получим:
(x0) 2 (-α) 0 (+α) 0 = (x0) 2 (n1),
(x0) 2 (n1) + (2x0x-2 + x-12, 2x0х-1+2x-2x1, 2x-2x2 +2x-1x1, 2x0х1+2x-1x2, 2x0х2+ х12) = (2x0x-2 + x-12, 2x0х-1+2x-2x1,x02 +2x-2x2 +2x-1x1, 2x0х1+2x-1x2, 2x0х2+ х12), что в точности совпадает с алгебраическим выражением.
6. Симметрия бесконечно малых и бесконечно больших координат
Попробуем определить функцию sin на поличисле α = (х-1,х0,х1). Здесь имеем:
— α = (x-1,0,0),
+α = (0,0,x1),
sin (х-1,х0,х1) = ∑1p=0 (sin (p) (x0) /p!) ∑pk=0 (p!/k! (p-k)!) (-α) p-k (+α) k = (sin (0) (x0) /0!) ∑0k=0 (0!/k! (0-k)!) (-α) 0-k (+α) k + (sin (1) (x0) /1!) ∑1k=0 (1!/k! (1-k)!) (-α) 1-k (+α) k = (sin (x0) (0!/0! (0—0)!) (-α) 0 (+α) 0 + cos (x0) ((1!/0! (1—0)!) (-α) 1—0 (+α) 0+ (1!/1! (1—1)!) (-α) 1—1 (+α) 1) = (sin (x0) (n1) + cos (x0) ((-α) + (+α)) = (cos (x0) x-1, sin (x0), cos (x0) x1).
Итак,
sin (х-1,х0,х1) = (cos (x0) x-1, sin (x0), cos (x0) x1).
Отсюда возникает предположение: не является ли и в общем случае выражение для функции на поличисле симметричным для бесконечно больших и бесконечно малых координат?
Покажем, что это в самом деле так.
Для этого нужно выражение (f) для функции на поличисле представить как координатную сумму.
f (α) = ∑np=0 (f (p) (x0) /p!) ∑pk=0 (p!/k! (p-k)!) (-α) p-k (+α) k.
∑pk=0 (p!/k! (p-k)!) (-α) p-k (+α) k = (p!/0! (p-0)!) (-α) p-0 (+α) 0 +
+ (p!/1! (p-1)!) (-α) p-1 (+α) 1 + … +
(p!/ (p-1)! (p- (p-1))!) (-α) p- (p-1) (+α) p-1 + (p!/p! (p-p)!) (-α) p-p (+α) p =
(p!/0!p!) (-α) p (+α) 0 + (p!/1! (p-1)!) (-α) p-1 (+α) 1 + … +
(p!/ (p-1)! (p- (p-1))!) (-α) 1 (+α) p-1 + (p!/p!0!) (-α) 0 (+α) p
Отсюда мы видим, что на каждое слагаемое (p!/k! (p-k)!) (-α) p-k (+α) k имеется симметричное слагаемое
(p!/ (p-k)! (p- (p-k))!) (-α) p- (p-k) (+α) p-k = (p!/ (p-k)!k!) (-α) k (+α) p-k.
Теперь нужно показать, что
∀m=-n,…,n (((-α) p-k (+α) k) m =f ((-α) k (+α) p-k) -m),
где =f — некоторый вид эквивалентности (эквиформности).
Здесь имеем:
(-α) p-k (+α) k = (∑nm=1,k1+2k2+...+nkn=m,k0+k1+k2+...+kn=p-k,kj≥0((p-k)!/k0!k1!k2!...kn!) x0k0x-1k1x-2k2…x-nkn) · (∑nm=1,k1+2k2+...+nkn=m,k0+k1+k2+...+kn=k,kj≥0(k!/k0!k1!k2!...kn!) x0k0x1k1x2k2…xnkn)
При х0 = 0 и k0≠0 всё слагаемое также нулевое, поэтому в сумме остаются только члены с k0=0, когда х0k0 = 00 = 1. В итоге можем записать:
(-αp-k (+α) k = (∑nm=1,k1+2k2+...+nkn=m,k1+k2+...+kn=p-k,kj>0((p-k)!/k1!k2!...kn!) x-1k1x-2k2…x-nkn) · (∑nm=1,q1+2q2+…+nqn=m,q1+q2+…+qn=k, qj> 0 (k!/q1!q2!…qn!) x1q1x2q2…xnqn).
Также перепишем сумму для отрицательных m в случае степеней -α и раскроем скобки:
(-α) p-k (+α) k = (∑-1m=-n,k1+2k2+...+nkn=-m,k1+k2+...+kn=p-k,kj>0((p-k)!/k1!k2!...kn!) x-1k1x-2k2…x-nkn) · (∑nm=1,q1+2q2+…+nqn=m,q1+q2+…+qn=k, qj> 0 (k!/q1!q2!…qn!) x1q1x2q2…xnqn) =
= ∑nm=-n,-k1-2k2-...-nkn+q1+2q2+...+nqn=m,k1+k2+...+kn=p-k,q1+q2+...+qn=k,kj>0,qj>0((p-k)!/k1!k2!...kn!) (k!/q1!q2!…qn!) (x-1k1x-2k2…x-nkn) (x1q1x2q2…xnqn).
Что же касается произведений (-α) k (+α) p-k, то здесь аналогично получим:
(-α) k (+α) p-k = ∑nm=-n,-k1-2k2-...-nkn+q1+2q2+...+nqn=m,k1+k2+...+kn=k,q1+q2+...+qn=p-k,kj>0,qj>0(k!/k1!k2!...kn!) ((p-k)!/q1!q2!…qn!) (x-1k1x-2k2…x-nkn) (x1q1x2q2…xnqn).
Для одной координаты m получим для (-α) p-k (+α) k
((p-k)!k!)/(k1!k2!...kn!) (q1!q2!…qn!) (x-1k1x-2k2…x-nkn) (x1q1x2q2…xnqn),
где -k1—2k2-… -nkn+q1+2q2+…+nqn=m, k1+k2+…+kn=p-k, q1+q2+…+qn=k, kj> 0, qj> 0.
С другой стороны, для противоположной координаты -m для (-α) k (+α) p-k будем иметь:
(k!/k1!k2!...kn!) ((p-k)!/q1!q2!…qn!) (x-1k1x-2k2…x-nkn) (x1q1x2q2…xnqn),
где -k1—2k2-… -nkn+q1+2q2+…+nqn=-m, k1+k2+…+kn=p-k, q1+q2+…+qn=k, kj> 0, qj> 0.
Условие -k1—2k2-… -nkn+q1+2q2+…+nqn=-m равносильно k1+2k2-…+nkn-q1—2q2-… -nqn=m. Если поменять символы q и k, то мы в точности получим условие для m-й координаты произведения (-α) p-k (+α) k.
Отсюда следует, что произведения (-α) p-k (+α) k и (-α) k (+α) p-k имеют эквиформные значения (с точностью до замен xm на x-m) для координат m и -m, что приведёт к эквиформности координат m и -m и для функции f (α) на поличисле α.
7. Общая формула для степенных функций на полных поличислах
Выше было показано, что если α = {xi} 0i=-n, то
∀m=0, -1,…, -n ((s (α∙α∙ … ∙α)) m = (<Tp [f] (sα)> n) m),
где α∙α∙ … ∙α — произведение поличисла α на себя р раз, f (x) = xp, Tp [f] — ряд Тейлора от функции f до членов степени р.
Также была определена функция f на поличисле α:
(f) ⠀f (α) = f (0α + -α + +α) = f (0α + (-α + +α)) = ∑np=0 (f (p) (x0) /p!) (-α + +α) p = ∑np=0 (f (p) (x0) /p!) ∑pk=0 (p!/k! (p-k)!) (-α) p-k (+α) k.
Но теперь нужно показать, что это определение совпадает с адгебраическими операциями для степенных функций на полных поличислах, а не только бесконечно малых, т.е. нужно показать, что
если α = {xi} ni=-n, то
∀m=-n,…,0,…n ((s (α∙α∙ … ∙α)) m = (<Tp [f] (sα)> n) m),
где α∙α∙ … ∙α — произведение поличисла α на себя р раз, f (x) = xp, Tp [f] — ряд Тейлора от функции f до членов степени р.
Здесь также будем использовать представление поличисла α в виде
α = 0α + -α + +α
и формулу полинома Ньютона:
(x1 + x2 + … +xm) n = ∑kj≥0,k1+k2+...+km=n(n!/k1!k2!...km!) x1k1x2k2…xmkm.
Тогда
sα = s0α + s-α + s+α,
sαp = ((s0α + s-α) + s+α) p = ∑pk=0 (p!/k! (p-k)!) (s0α + s-α) k (s+α) p-k.
Тогда имеем:
(∑ni=-nxi) p = ∑k (i) ≥0, {∑ni=-n (k (i))} = p (p!/Пni=-nk (i)!) Пni=-nxik (i) — полином Ньютона,
∑nm=-n∑k (i) ≥0, {∑ni=-n (k (i))} = p,∑ni=-n (ik (i))} = m (p!/Пni=-nk (i)!) Пni=-nxik (i) — координатное представление полинома Ньютона по координате i от i=-n до i=n.
Имеем:
(**) (∑ni=-nxi) p =n ∑nm=-n∑k (i) ≥0, {∑ni=-n (k (i))} =p,∑ni=-n (ik (i))} =m (p!/Пni=-nk (i)!) Пni=-nxik (i) — полином Ньютона n-равен (по координате i от i=-n до i=n) своему координатному представлению по координате i от i=-n до i=n.
Уточнив представление для полинома Ньютона, теперь подобное же уточнение нужно будет сделать для ряда Тейлора.
Для ряда Тейлора можем записать:
f (sα) = f (∑ni=-nxi) = f (x0 + ∑-1i=-nxi + ∑ni=1xi) = ∑nk=0 (f (k) (x0) /k!) (∑-1i=-nxi + ∑ni=1xi) k = ∑nk=0 (f (k) (x0) /k!) (∑ni=-nxi) k|xi≠0 = ∑nk=0 (f (k) (x0) /k!) ∑nm=-n∑k (i) ≥0, {∑ni=-n (k (i))} =k,∑ni=-n (ik (i))} = m (k!/Пni=-nk (i)!) Пni=-nxik (i) |xi≠0.
При f (x) = xp имеем:
f (sα) = ∑pk=0 ((p!/ (p-k))!x0p-k/k!) ∑nm=-n∑k (i) ≥0, {∑ni=-n (k (i))} =k, {∑ni=-n (ik (i))} = m (k!/Пni=-nk (i)!) Пni=-nxik (i) |xi≠0 = ∑pk=0∑nm=-n∑k (i) ≥0, {∑ni=-n (k (i))} =k, {∑ni=-n (ik (i))} = m ((p!/ (p-k))!x0p-kПni=-nk (i)!) Пni=-nxik (i) |xi≠0.
Обозначим k (0) = p-k. Тогда р = k (0) +k, и из условия
{∑ni=-n (k (i))} |i≠0=k
прибавлением к обеим сторонам k (0) получим:
{∑ni=-n (k (i))} =k+k (0) = p.
Также условие
{∑ni=-n (ik (i))} |i≠0=m
эквивалентно условию
{∑ni=-n (ik (i))} =m,
поскольку ik (i) = 0 при i=0.
Также варьирование k от нуля до р будет эквивалентно варьированию k (0) от нуля до р, что как раз выражено условием {∑ni=-n (k (i))} = p, так что суммирование по k можно снять.
В итоге последнее выражение для ряда Тейлора мы можем переписать в следующем виде (для f (x) = xp):
(Т) f (sα) = ∑nm=-n∑k (i) ≥0, {∑ni=-n (k (i))} =р, {∑ni=-n (ik (i))} = m ((p!/k0))!x0k0Пni=-nk (i)!) Пni=-nxik (i) = ∑nm=-n∑k (i) ≥0, {∑ni=-n (k (i))} =р, {∑ni=-n (ik (i))} = m (p!/Пni=-nk (i)!) Пni=-nxik (i),
что полностью совпадает с выражением (**) для полинома Ньютона.
Здесь только остаётся показать, что k (0) = p-k для представления через ряд Тейлора — то же k (0), что в представлении через полином Ньютона. Это следует из условия
∑ni=-n (k (i)) =p
для представления (**) и условия
{∑ni=-n (k (i))} |i≠0=k
для представления через ряд Тейлора.
В самом деле, здесь имеем:
∑ni=-n (k (i)) |i≠0 + k (0) = ∑ni=-n (k (i)) = p,
откуда получаем:
k + k (0) = p, т.е.
k (0) = p-k.
Итак, мы доказываем более общую теорему:
Теорема 2.
Если α = {xi} ni=-n, то
∀m=-n,…,0,…n ((s (α∙α∙ … ∙α)) m = (<Tp [f] (sα)> n) m),
где α∙α∙ … ∙α — произведение поличисла α на себя р раз, f (x) = xp, Tp [f] — ряд Тейлора от функции f до членов степени р.
8. Обобщённо-инверсная интерпретация поличисел
При симметричной интерпретации поличисло α = {xi} ni=-n в связи с определением на нём функций будем понимать как центральное значение х0, относительно которого определяются прямые и обратные приращения.
Чтобы определить реализацию поличисла, используя его симметричную интерпретацию, рассмотрим вариант α = {xi} 2i=-2 из 2-предполя 2F.
Здесь имеем:
α = (x-2,x-1,x0,x1,x2).
Определим далее реализацию для дифференциальной части:
r-2 (d2x-2 +’ dx-1 +’ x0) = x0 + Rm1 (x-1 + R-1m2 (x-2)) =
= R-1m1 (x0) oR-1m2 (x (-1)) (x-2),
где R-1m (а) (х) = а + R-1m (х).
В общем случае для дифференциальной части {xi} 0i=-n поличисла α = {xi} ni=-n получим:
r-2 ({xi} 0i=-n) = [Сni=1R-1mi (x (1-i))] (x-n)
Запишем нечто подобное для интегральной части. Сначала запишем вид реализации, аналогичный дифференциальной части для n=2:
х2 + R-1M1 (х1 + R-1M0 (x0)),
а затем подействуем на неё оператором обобщённой инверсии Iv:
Iv (х2 + R-1M1 (х1 + R-1M0 (x0))) = Iv (R-1M1 (х2) oR-1M0 (х1) (x0)) =
= Iv (х2) + *Iv (R-1M1 (х1 + R-1M0 (x0))).
Как и ранее, будем использовать функцию IR-1M (Iv (α)) = IvoR-1M (α). Тогда можем записать:
Iv (х2) +* Iv (R-1M1 (х1 + R-1M0 (x0))) = Iv (х2) +* IR-1M1 (Iv (х1 +
+R-1M0 (x0)))) = Iv (х2) +* IR-1M1 (Iv (х1) +* IvoR-1M0 (x0))) =
= Iv (х2) +* IR-1M1 (Iv (х1) +* IR-1M0 (Iv (x0))) =
= х2* +* IR-1M1 (х1* +* IR-1M0 (x0*)) = [С1i=2IR-1М (i-1) (хi*)] (х0*),
где IR-1Мi (хi*) = хi* +* IR-1Мi, и оператор обобщённой инверсии определён для шкалы величин х2.
Посмотрим, как будет выглядеть такая реализация графически.
Первоначально мы находимся во внутренней метрике системы обратного конечного количества Q (0) *, и здесь имеем величину х0. Далее переходим к внутренней обратной метрике системы бесконечно больших величин первого порядка Q (1) *, где имеется величина х1. Система Q (0) * проецируется в систему Q (1) * обратной R-функцией R-1М0, в итоге здесь получаем величину х1 + R-1М0 (х0). Теперь мы получаем количественную систему Q (0,1) *, в которой скоординированы системы Q (0) * и Q (1) *. Далее ситуация повторяется, и для внутренней метрики системы бесконечно большого количества второго порядка Q (2) * получаем величину у = х2 + R-1М1 (х1 + R-1М0 (х0)), образуя систему Q (0,1,2) *, в которой скоординированы системы Q (0) *, Q (1) * и Q (2) *. Полученная величина у — это величина ∞у, данная во внутренней метрике обратного количества. Чтобы получить её представление в системе прямого количества IvQ (0,1,2) *, действуем на неё оператором обобщённой инверсии Iv, определённом для количественной системы Q (0,1,2) *. Получаем величину Iv (у) ∞, где
Iv (y) = Iv (х2 + R-1М1 (х1 + R-1М0 (х0))) = х2* +* IR-1M1 (х1* + *IR-1M0 (x0*)) =
= [С1i=2IR-1М (i-1) (хi*)] (х0*).
Все эти преобразования можно следующим образом представить графически — см. рис. 10.
Эти преобразования аналогичны таковым для конечной и бесконечно малых количественных систем, но в случае кнечной и бесконечно больших систем мы исходно движемся во внутренней метрике этих систем как систем обратного количества и лишь на конечном этапе переходим к прямой метрике.
Отсюда становится понятной общая форма реализации интегральной части для поличисла α∈nF. Это реализация вида
[С1i=nIR-1М (i-1) (xi*)] (х0*).
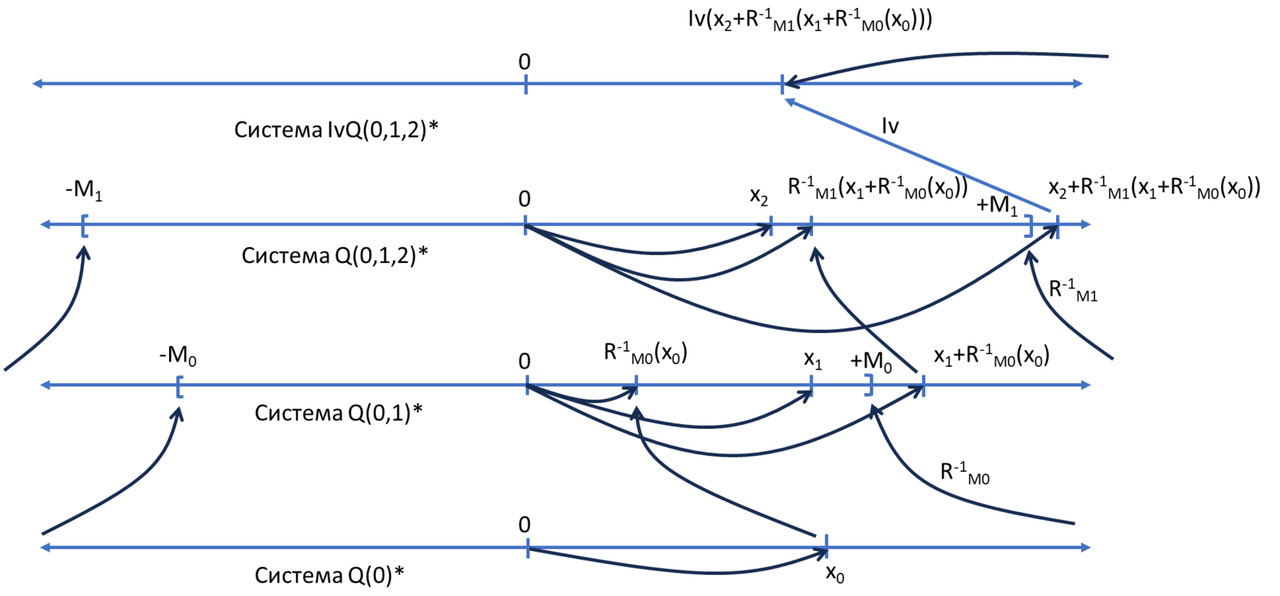
Наконец, определим полную симметричную реализацию поличисла α в следующем виде:
r±n {xi} ni=-n = ([Сni=1R-1mi (x (1-i))] (x-n), [С1i=nIR-1М (i-1) (xi*)] (х0*)),
где оператор обобщённой инверсии определён для количественной системы Q (0,…,n) *.
9. К структуре бесконечного расширения n-предполя nF
В монографии «Логика открытого синтеза» я ранее развил определённую версию R-анализа, исследуя бесконечные в обе стороны поличисла
α = {xi} ∞i=-∞
с тем условием, что для каждого поличисла найдётся максимальная ненулевая координата xn, а все координаты xm, где m> n, будут нулевыми. Таким образом, это поличисла, которые могут обладать бесконечным числом ненулевых координат в дифференциальной своей части, но всегда имеют нулевое или конечное число ненулевых координат в интегральной части.
Множество таких поличисел было обозначено как ∞F, и для него не существует делителей нуля, и для каждого поличисла α можно находить всё большее число координат для поличисла α-1, так что в этом предельном случае мы имеем дело не с предполем, а именно с полем. Было показано выполнение основных свойств операций сложения и умножения, характерных для структуры поля, введено отношение порядка, как это было сделано и для предполя nF, доказана теорема Архимеда.
Поле ∞F можно рассматривать как предельный случай предполя nF при n→∞.
В качестве реализации поличисел из ∞F был принят следующий случай:

Была доказана теорема, что при определённых требованиях к обратным R-функциям μ (α) является конечным числом. Показано также, что множество ∞F может быть рассмотрено как гильбертово пространство.
Были рассмотрены также подпространства nmF, где n≥m и α∈nmF е.т.е. ∀i∀j (i> n ∧ j <m ⊃ αi=0 ∧ αj=0). Для элементов α∈nmF были введены следующие реализации:
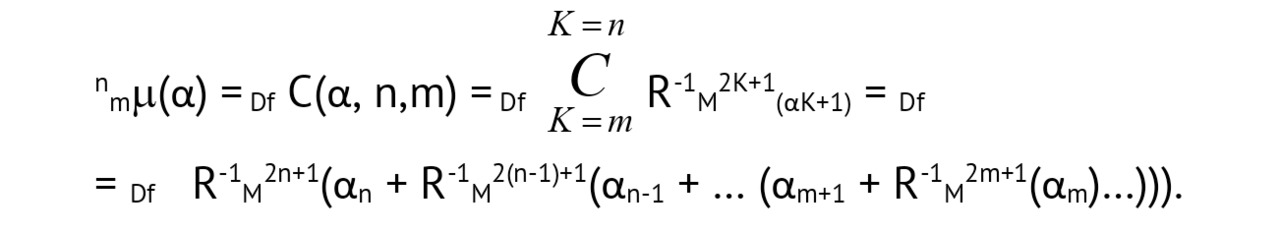
Отсюда видно, что это реализации иерархического типа.
В целом, была проделана достаточно большая работа по определению структуры ∞F и её расширения на комплексный случай.
Имея в виду возможность симметричной и иерархической интерпретации поличисел, теперь можно отметить только тот момент, что алгебра поличисел в «Логике открытого синтеза» строилась на основе симметричной интерпретации, а реализация поличисел предполагала иерархическую интерпретацию. Но поскольку вторая может быть рассмотрена как частный случай первой, то все конструкции остаются в силе. Следует только уточнить, что если поличислу α мы даём иерархическую реализацию, то и алгебраически его нужно представить так, чтобы в нём не встречались одновременно интегральные и дифференциальные координаты, т.е. все координаты, кроме нулевой, должны быть либо дифференциальными, либо интегральными. В частности, поскольку бесконечные поличисла α∈∞F могут иметь бесконечное число ненулевых координат только в дифференциальную сторону, то и алгебраически их ненулевые координаты все должны быть только дифференциальными. Все ненулевые интегральные координаты возможны только для конечных поличисел α∈nmF.
Все эти структуры вполне можно включить в «Основы R-анализа», рассматривая как вариант бесконечного обобщения структур n-предполя nF, но повторять их здесь я не буду и отсылаю заинтересованного читателя к указанной монографии.
10. Стандартный математический анализ как частный случай R-анализа
Используя конструкции R-анализа как исчисления поличисел, можно с помощью этих средств попытаться представить конструкции стандартного математического анализа.
Пусть мы работаем с R-анализом в рамках поличисел α∈nF, где n≥1. В этом случае мы можем использовать следующий естественный принцип соответствия: вещественное число х в стандартном математическом анализе моделируется как поличисло α = {xi} ni=-n, где х = х0, а все остальные координаты α нулевые. Такие поличисла обозначим как α (х). На поличислах α (х) n-предполе nF переходит в обычное поле 0F вещественных чисел, и все конструкции стандартного анализа тривиально воспроизводятся. Например, если у = f (x1,…,xn) — некоторая n-местная вещественная функция, то может быть определена функция f* на поличислах α (х) такая, что
f* (α1 (x1),…,αn (xn)) = α (f (x1,…,xn)).
Аналогично, если Р — n-местный предикат на вещественных числах, то может быть определён его аналог Р* такой, что
P* (α1 (x1),…,αn (xn)) истинен е. т. е. Р (x1,…,xn) истинен.
В то же время для ряда конструкций стандартного анализа можно определить более богатые поличисловые определения, которые затрагивают ненулевые координаты поличисел.
Пусть, например, в рамках стандартного математического анализа дана предельная последовательность {xn} ∞n=1, где limn→∞xn = x. Тогда можно принять следующее соотношение в 1F:
limn→∞ (0,xn,0) = (y, limn→∞xn,0),
где y = limn→∞ (nxn).
В частности, если xn = 1/n, то получим:
limn→∞ (0, (1/n),0) = (y,0,0), где
y = limn→∞ (n (1/n)) = 1, т.е.
limn→∞ (0, (1/n),0) = (1,0,0).
Полная запись будет такой:
limn→∞ (0,xn,0) = (limn→∞ (n (xn)),limn→∞xn,0).
Тем самым мы выражаем ту идею, что предельная последовательность даёт не только 0-координату, но и (-1) -координату поличисла.
Последовательность {1/n} ∞n=1 является эталонной в том смысле, что она даёт в пределе единицу бесконечно малых величин.
Для бесконечно больших последовательностей {xn} ∞n=1, где limn→∞xn = ∞, примем следующее соотношение:
limn→∞ (0,xn,0) = (0,0,р),
где р = limn→∞ (xn/n).
В этом случае эталонной окажется последовательность {n} ∞n=1, которая будет давать бесконечно большую единицу:
limn→∞ (0,n,0) = (0,0,1).
Переходя к непрерывному случаю, примем следующие соглашения:
если limх→0f (x) = 0, то
limх→0 (0,f (x),0) = (y,0,0),
где y = limx→0 (f (x) /x).
В частности, получим:
limx→0 (0,x,0) = (1,0,0).
Пусть функции f (x) и g (x) имеют конечные пределы в х0, т.е. limx→x0f (x) = X∈R и limx→x0g (x) = X»∈R. Тогда примем, что
limx→x0 (0,f (x),0) = (y, limx→x0f (x),0) = (у,Х,0),
limx→x0 (0,g (x),0) = (y’,limx→x0g (x),0) = (y’,X», 0),
где
|y/y’| = limx→x0 (|Х-f (x) / (X» — g (x) |).
Пусть функции f (x) и g (x) имеют бесконечный предел в х0, т.е. limx→x0f (x) = ± ∞ и limx→x0g (x) = ±∞. Тогда примем, что
limx→x0 (0,f (x),0) = (0,0,±p).
limx→x0 (0,g (x),0) = (0,0,±p’), где
p, p’> 0,
р/р» = limx→x0 (f (x) /g (x)).
Будем называть функцию f (y,x,0) = (у», x’, 0) 0-непрерывной в точке х е. т. е. limx→x0 (0, f (x), 0) = (у, f (x0), 0).
Будем называть функцию f (y,x,0) = (y’,x’,0) (0, -1) — непрерывной в точке х е. т. е. верно, что f (y,x,0) = (y’,f (x),0).
Если вещественная функция у = f (x) дифференцируема в точке х, то примем следующее соотношение:
limΔx→0 (0,f (x+Δx),0) = (limΔx→0f (x+Δx) /Δx, limΔx→0f (x+Δx),0) = (df (x) /dx, f (x),0).
Если вещественная функция у = f (x) дифференцируема в точке х, то определим оператор дифференцирования d для тричисла (0,f (x),0) следующим образом:
d (0,f (x),0) = (df (x) /dx,0,0).
В частности,
d (0,x,0) = (1,0,0).
Отсюда для дифференцируемой функции получаем:
limΔx→0 (0,f (x+Δx),0) = (0,f (x),0) + d (0,f (x),0).
Также несколько слов по поводу интерпретации дельта-функции.
Примем следующее важное соотношение:
δ (x’-x) = (0,0,e (x’,x)), где
e (x’,x) = 1 при x’=x, и e (x’,x) = 0 при x’≠x.
Для основного свойства дельта-функции
∫f (x’) δ (x’-x) dx’ = f (x)
примем следующую интерпретацию:
∫f (x’) δ (x’-x) dx’ = ∑x’∈Rf (x’) (0,0,e (x’,x)) (1,0,0) = ∑x’∈Rf (x’) (0,e (x’,x),0) = ∑x’∈R (0,f (x’) e (x’,x),0) = (0,∑x’∈Rf (x’) e (x’,x),0) = (0,f (x),0) = f (x).
Таким образом, мы интерпретируем дельта-функцию как бесконечно большую единичную функцию, которая принимает бесконечно большую единицу (0,0,1) при х»=x и равна нулю (0,0,0) при x’≠x. В этом случае интеграл играет скорее символическую роль и может быть заменён на бесконечную сумму.
В такой манере можно и далее развивать координации стандартного математического анализа и R-анализа, согласовывая между собой подходы Ньютона, основанного на теории пределов, и Лейбница, предполагающего актуальность бесконечных величин.
11. К многомерным версиям R-анализа
Ещё одно возможное расширение R-анализа — построение его векторных версий, т.е. продолжение структур R-анализа на случай многомерных векторных пространств.
Рассмотрим принципы такого продолжения пока на примере трёхмерного пространства.
Пусть дано вещественное 3-мерное пространства П» = R3 со скалярным произведением.
На элементах R3 определена стандартная векторная алгебра с операциями сложения и внешнего умножения на вещественные числа.
Будем использовать векторные R-функции, где обратная R-функция R-1П* изоморфно сжимает прообразное 3-мерное пространство П в конечный объём П*, являющийся подмножеством пространства П». Как и в случае скалярного варианта, потребуем, чтобы функция R-1П* была непрерывной и при П*→П переходила в тождественное отображение.
В объёме П*, который также можно называть R-пространством, можно воспроизвести структуру векторного пространства П, используя R-изоморфизм:
⋅ если f — n-местная операция на векторах в пространстве П, то f* — её R-аналог, и f* (x1*,…,xn*) = (f (x1,…,xn)) *, где х* = R-1П* (х),
⋅ если P — n-местный предикат на векторах в пространстве П, то Р* — его R-аналог, и Р* (x1*,…,xn*) е.т. е. Р (x1,…,xn).
В R-пространстве П* появляется внешняя форма и какая-то связанная с нею геометрия, для которой может существовать наиболее органичная система координат. Например, П* может иметь форму шара, и тогда в качестве его органичной системы координат вполне логично рассматривать сферическую систему координат. Такие органичные для внешней геометрии системы координат R-пространств будем называть собственными или естественными системами координат.
Введение естественной системы координат для R-пространства П* приводит к переносу этой координатной системы и на прообразное пространство П действием прямой R-функции R+1П*. Это значит, что в прообразном пространстве также появляется преимущественная система коодринат, выделенная относительно всех остальных координатных систем, которую также можно называть «естественной» или «собственной», но уже для прообразного пространства П. Тогда у R-пространства П* должен быть и свой центр, в качестве которого выступает ноль собственной системы координат пространства П*.
Векторы в П получают своё координатное представление в собственной системе координат, и в этом случае векторную R-функцию можно связать со скалярными функциями, действующими для каждой координаты.
Например, если R-пространство П* имеет форму шара, и с нею в прообразном пространстве П связана сферическая система координат (r, θ, φ), где r — полярный радиус, θ — зенитный и φ — азимутальный углы, то векторную R-функцию можно определить в данном случае очень просто — она сжимает полярный радиус и оставляет неизменными углы:
R-1П* (r, θ, φ) = (R-1М (r), θ, φ),
где R-1М — обратная базовая скалярная R-функция.
В этом случае сферическое R-пространство П* будет иметь центр в точке 0 пространства П» и радиус М. Такое R-пространство можно обозначить символом П* (0). Другие подобные R-пространства с центрами в точках х можно получать переносом на х R-пространства П* (0), т.е.
П* (х) = х + П* (0) = х + R-1П* (П) = R-1П* (х) (П).
В связи с введением собственных систем координат для R-пространств, мы можем в R-пространствах определить понятие обратного вектора и задать алгебру на обратных векторах, обобщая алгебру обратного количества, рассмотренную ранее.
Например, если имеется R-вектор х* = (r*, θ, φ), где r* = R-1М (r), в сферическом R-пространстве П* (0), то ему можно сопоставить обратный вектор х*М = (r*М, θ, φ), где r*М = R-1М (r∞). Геометрически ему можно сопоставить вектор величиной М — r* с углами θ, φ в R-пространстве П* (0), но отложенный от поверхности R-пространства П* (0) в сторону центра этого пространства (см. рис. 11).
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.