Бесплатный фрагмент - Понять Искусственный Интеллект

Введение

В книге рассказывается про историю появления идеи искусственного интеллекта (ИИ), а также про попытки эту идею реализовать. Этому посвящена первая глава книги.

Начиная со второй главы — рассказывается об основных инструментах и подходах, которые лежат в основании ИИ. Данные базовые идеи, но подробно, в том числе с подробными математическими выкладками. Задача этих глав — показать, из каких «зерен» прорастают нейронные сети, которые стали называть искусственным интеллектом в наше время.

В отличие от большинства книг по ИИ у нас нет задачи обучить созданию нейронных сетей, рассказать о всяких сложных техниках машинного обучения. Все это важные темы, но они — всего лишь развитие тех базовых идей, которым и посвящена наша книга. Усвоив базовые идеи, о которых рассказано в книге, вы сможете самостоятельно разобраться в любых современных подходах по построению ИИ.

Такой подход — сознательное решение. Обучение должно строиться через усвоение элементарных оснований и диалектического метода, когда человек умеет искать и находить развитие, движение этих элементарных оснований. Затем знание о методе прикладывается к реальным задачам, в работе над которыми и осуществляется дальнейшее изучение.

Кода в книге нет, весь код вынесен в репозиторий на GitHub.

Раздел 1 История искусственного интеллекта

История искусственного интеллекта — это часть истории развития промышленности и идей, возникающих в связи с этим развитием. Когда капитализм возник и стал укрепляться в 16 веке, зародилась современная физика, математика, философия. Идеи же физики, математики, философии стали развиваться и применительно к человеку. Мир вообще, человек в частности стали восприниматься как объекты научного внимания. Однако наука в капиталистический период своего развития смотрит на человека антидеалектично, то есть не принимает во внимание историю, развитие, движение объекта изучения. Только в 19 веке появляются и укрепляются идеи диалектики, начинают искать за каждым объектом научного исследования его историю, развитие. Однако направление это, учитывая господство капитализма, не стало основным. Конечно, ученые были вынуждены, чисто объективно, учитывать развитие мира в своих исследованиях, но они делали все возможное, чтобы свести развитие мира, человека к простому изменению. Поэтому еще Гоббс писал: «рассуждение есть не что иное, как подсчитывание».

Именно на этом фоне возникают представления об «искусственном интеллекте». Сам термин появится только в середине 20 века. До этого должно было произойти нечто важное — должна была возникнуть электротехника, передача электрической энергии. Появление этих отраслей промышленности подстегнуло развитие всей остальной промышленности. Управление, как передачей электроэнергии для огромных заводов, так и управление самим производством, привело к появлению автоматики. Автоматы, управляя электроэнергией, заводами, сами же и потребляли электроэнергию. Это взаимное влияние только подстегивало развитие как автоматики, так и применения электроэнергии.

Так как работают на заводах люди, то и применение автоматики, новых машин непременно приводило к взаимодействию человека и автоматики. Постепенно стал возникать своеобразный симбиоз человека и машины. Особенно это стало развиваться в военном деле, для чего первая половина 20 века давала много оснований. Применение современного оружия требовало сложных математических расчетов. На такие расчеты тратилось много труда. Еще в конце 19 века в США появляются средства автоматизации расчетов, применяемые в промышленных масштабах. Однако в 20 веке и они уже не справлялись с возросшим объемом расчетов. Тогда постепенно возникает задача, а затем и решение, — электронная вычислительная машина (ЭВМ). Возникает не на пустом месте, развитие автоматики, электроэнергии, науки дает те средства, которые можно использовать для решения поставленной задачи.

Возьмем книгу 1958 года «Автоматические цифровые машины» от авторов Н. А. Архангельского, Б. И. Зайцева. Посмотрим, чем были ЭВМ в те первые десятилетия, когда только зародились и начинали свое развитие.

Вычислительные машины, пишут авторы, могут быть «непрерывного действия» и «цифрового действия». Непрерывность означает, что вычислительная машина измеряет физические величины, которые принимаются непрерывными. Например, напряжение можно бесконечно делить, но нельзя исчерпать таким делением, напряжение — непрерывно. Машины «цифрового действия» работают не с непрерывными величинами, а, напротив, с величинами дискретными, «прерывными». Например, счеты можно считать вычислительной машиной, которая ведь иметь «прерывные» величины — костяшки. Любопытно, что этими дискретными значениями можно описать непрерывные процессы. Так, никто не мешает нам считать непрерывное напряжение на «прерывных» счетах.

Традиционно в истории «цифровых машин» много внимания обращают на «аналитическую машину» Беббиджа, которая была задумана еще в 19 веке. Вот как авторы описывают ее принцип работы: «По идее Беббиджа „Аналитическая машина“ должна была обладать следующими особенностями: выполнять простые арифметические действия; запоминать начальные данные, промежуточные данные и результаты вычислений; запоминать группу инструкций или команд, по которым должно выполняться решение задачи; выдавать результаты вычислений и последовательно выполнять команды заданной программы вычислений. Особый интерес представляла заложенная в машину способность автоматически прекращать вычисления при выполнении некоторых условий. Если такое условие не было достигнуто при первом выполнении программы, то цикл вычислений повторялся.»

Как видим, во всем основном машина Беббиджа вполне напоминает современные ЭВМ. Со времен Беббиджа вычислительные машины постепенно развивались. До 1937 главным образом развивались счетно-аналитические машины, особенностью которых было использование перфокарт.

В 1937 Говард Айкен переоткрывает идеи Беббиджа, а Тьюринг формулирует идею универсальной машины. В 1944 была построена релейная цифровая вычислительная машина Марк I. Особенностью этой машины было наличие памяти, в которой хранились промежуточные и окончательные результаты вычислений. Вскоре появилась машина Марк II. Эти машины были построены на релейных схемах, однако удобного способа составления таких схем не было. В это время Шеннон предлагает использовать булеву алгебру для анализа релейно-контактных схем.

Использование электромеханических реле уменьшало надежность вычислительных машин. В 1943 появляется вычислительная машина Эниак, в которой использовались уже электронные реле. Если электромеханическое реле выдерживало только миллион переключений, то электронные реле выполняли миллион переключений в одну секунду. Однако проблемой Эниак было то, что подготовка к вычислениям, когда нужно было вручную запрограммировать машину, занимало настолько большое количество времени, что выигрыш во времени вычислений практически не имел значения.

В 1947 Нейман предлагает подход, когда непосредственно в машину вводилась программа, которая к тому же могла изменяться самой машиной при проведении вычислений. С этих пор и начинается уверенное развитие ЭВМ.

Итак, на каких же принципах работает ЭВМ? В конечном счете, пишут авторы, любая задача сводится к арифметическим действиям. Поэтому основной частью машины является арифметическое устройство, которое выполняет эти арифметические действия, а также ряд дополнительных, например нахождение целой части числа. Кроме этой, основной части, ЭВМ имеет устройства ввода и вывода, запоминающее устройство, а также устройство управления, которое следит за работой всех остальных элементов. В ЭВМ используют двоичную систему счисления. Вот что пишут авторы: «В современной машинной математике особое место заняла система записи чисел с основанием „два“. Это связано с тем, что многие элементы быстродействующих машин, как, например, электронное реле, могут иметь два устойчивых состояния: „включено“ и „выключено“. Если теперь условимся одно из состояний такого элемента, например „включено“, обозначить единицей, а другое состояние — нулём, то удобство изображения чисел в машине в двоичной системе станет понятным.»

Эти нули и единицы дают возможность применить булевую алгебру. Авторы пишут: «Если теперь попытаться составить такие электрические схемы, чтобы они могли выполнять основные действия булевой алгебры (логическое сложение, логическое умножение и логическое отрицание), то, пользуясь выведенными формулами, можно из этих схем составить новые схемы для выполнения куда более сложных действий. Другими словами, с помощью булевой алгебры можно синтезировать (т. е. составлять) вычислительные схемы дискретного действия и, скажем без стеснений, можно анализировать уже составленные схемы.»

На первом этапе конструирования ЭВМ создают логические схемы устройств, которые состоят из логических элементов и связей. На втором этапе составляют принципиальную схему логических элементов. Далее, в схеме заменяют логические элементы электронными схемами, что дает принципиальную схему ЭВМ.

Для логических операций «и», «или» могут быть разные схемы. Однако общий их смысл состоит в том, что на вход подаются значения от разных источников в форме 0 и 1, по специальным таблицам делается вывод о том, какое число должно получиться на выходе. В этом и состоит основа создания и работы ЭВМ. Компьютеры изначально изобретались для решения математических задач. Первые ЭВМ решали системы линейных уравнений.

Одновременно в науке 20 века крепнет позитивизм. Физика, как и математика, к концу 19 века оказались в кризисе. Антидиалектические теории о материи, на которых строились теории прошлого, сталкивались с реальностью, результатами экспериментов, открытий. Ученым приходилось подлаживать эти свои антидиалектические представления к новым данным. В начале 20 века это удалось кое-как сделать с помощью квантовой механики и теории относительности. Однако, чтобы квантовая механика и теория относительности «работали» нужно было усвоить себе позитивистский взгляд на мир. Что это означает? Это означает, что в расчет нужно принимать только «наблюдаемые величины», не надо пытаться объяснить причины того, как устроен мир. Нужно просто зафиксировать это «устройство» мира, определить те формальные законы, по которым этот мир изменяется, а дальше — просто считать. Знаменитый лозунг «заткнись и считай», который так нравился физику Фейнману, вполне передает идеологию, сидевшую в головах физиков и математиков 20 века.

И вот в 30-ых годах появляется Тьюринг со своей знаменитой машиной. Понятие машины Тьюринга появляется в его статье «О вычислимых числах, с приложением к проблеме разрешимости». Идеи Тьюринга сводились к тому, что если нечто можно вычислить, то вычислить это можно с помощью машины. Для этого нужно только создать алгоритм, который будет состоять из элементарных команд-операций. Выполнив эти команды, машина и получит решение.

Идеи эти сразу же пытаются приложить к человеку непосредственно. В 1943 году появляется «Логическое исчисление идей, имманентных нервной деятельности», авторами которой являются Мак-Каллок и Питтс. Здесь описывается модель искусственного нейрона, с помощью которого можно познать мир. Важно, что Питтс был ценителем «Принципов математики» Рассела, учился у Виннера, был связан с Карнапом. Все это были важные представители позитивизма в науке. Мак-Каллок не скрывал, что представлял себе мозг человека как машину Тьюринга.

Итак, в 50-ых годах у нас есть все элементы, которые и породили представления об искусственном интеллекте. Развитие промышленности привело к появлению автоматики, с которой человек все больше взаимодействовал. Это же развитие промышленности толкало вперед науку, которая все больше путалась в своих противоречиях, искала выход из них, находила его в позитивизме. Представления о человеке, через представления о «вычислимости», стали опускаться до уровня машины, а машины стали подниматься на уровень человека. Где-то эти движения должны были найти друг друга — и они нашли в кибернетике. В 1948 году появляется книга Винера «Кибернетика, или управление и связь в животном и машине». Так закрепляется представление о единстве процессов управления — человеком и машиной. Человека и машину стали рассматривать просто как системы, у которых есть общие элементы управления, обработки информации.

В это время появляется статья Тьюринга «Может ли машина мыслить?» (1950). Здесь появилась знаменитая «игра в имитацию». Проследим за мыслью автора.

Как образовалась эта формула мы видели. Здесь h_k (X) — скрытый нейрон (Hidden Unit).

Если бы мы не трансформировали h_k (X), то у нас получилась бы обычная линейная регрессия. Однако мы применяем какую-то нелинейную трансформацию — сигмоида или ReLU. Итак, еще раз посмотрим на это:

Если бы мы не трансформировали h_k (X), то у нас получилась бы обычная линейная регрессия. Однако мы применяем какую-то нелинейную трансформацию — сигмоида или ReLU. Итак, еще раз посмотрим на это:

«Кто-нибудь задающий вопросы» заменяется на машину. Правда, раз мы не знаем, что такое машина, то возможность такой замены под вопросом. Тьюринга это не смущает и даже не интересует. Его интересует, а будет ли машина ошибаться в ответе на вопрос, кто — мужчина, а кто — женщина, чаще человека.

Через несколько страниц, забыв, что определение «машины» он давать не хотел, Тьюринг все-таки пытается описать, что же является машиной. Он вводит ограничение, что машиной будет считаться только ЭВМ, а дальше дает описание этих ЭВМ.

ЭВМ, по мысли Тьюринга, заменяет человека-вычислителя. У человека-вычислителя есть сборник правил, которых он должен придерживаться при вычислении. Есть у него и неограниченный набор бумаги, чтобы проводить вычисления, а также арифмометр для операций сложения и умножения. В ЭВМ человек-вычислитель реализуется через 1) запоминающее устройство, 2) исполнительное устройство, 3) контролирующее устройство. Запоминающее устройство — это бумага вычислителя, исполнительное устройство — это механизм, позволяющий производить вычисления. Контролирующее устройство следит за тем, чтобы надлежащим образом выполнялась книга правил, по которым производятся вычисления. В ЭВМ эта книга правил называется «таблицей команд».

В запоминающем устройстве информация разбивается на части и хранится в отдельных ячейках, каждая из которых имеет свой номер. В таблице команд каждая команда отсылает к конкретной ячейке памяти, из которой нужно извлечь число, над которым затем производится арифметическая операция. Тьюринг особо выделяет команду выполнения условия. Вот пример такой команды: «Если ячейка 4505 содержит 0, выполнить команду, хранящуюся в ячейке 6707, в противном случае продолжать идти по порядку».

В итоге процесс выглядит так. Спрашиваем человека-вычислителя, как он производит вычисления. Разбиваем это на команды и заносим в таблицу команд. На основании таблицы команд ЭВМ производит вычисление.

ЭВМ являются «машинами с дискретными состояниями», то есть с отличимыми друг от друга состояниями. Мы подаем дискретные команды на вход машины, она, руководствуясь таблицей команд производит вычисления, на выходе машина выдает одно из дискретных состояний, например «включено», «выключено». ЭВМ являются «универсальными машинами», потому что ЭВМ может имитировать любую машину с дискретным состоянием.

Проследим путь Тьюринга. Он ставил вопрос о мышлении машины, не пытаясь дать определение ни машине, ни мышлению. Затем машина была описана так, что ее свойствами стали «дискретность» и «универсальность». Раз вопрос о мышлении машины был заменен вопросом о способностях машины, а способности машины описаны, как «дискретные» и «универсальные», то представление о мышлении свелось к «дискретности» и «универсальности». Таким ловким трюком мышление машины, которое предполагается равным мышлению человека, свелось к дискретности, а значит и мышление человека было сведено к дискретности. Итак, изначальный вопрос игры в имитацию теперь сводится к следующему: «Если взять только одну конкретную цифровую вычислительную машину Ц, то, спрашивается: справедливо ли утверждение о том, что, изменяя емкость памяти этой машины, увеличивая скорость ее действия и снабжая ее подходящей программой, можно заставить Ц удовлетворительно исполнять роль А в игре в имитацию» (причем роль В будет исполнять человек)?»

Ловко? Ловко. Вот оцените: «Первоначальный вопрос „могут ли машины мыслить?“ я считаю слишком неосмысленным, чтобы он заслуживал рассмотрения. Тем не менее я убежден, что к концу нашего века употребление слов и мнения, разделяемые большинством образованных людей, изменятся настолько, что можно будет говорить о мыслящих машинах, не боясь, что тебя поймут неправильно.»

Тьюринг в начале статьи всего лишь признал, что дать определение мышления и машины нельзя, теперь же он утверждает, что сам вопрос смысла не имеет. Смысл имеет только тот вопрос, который сформулировал Тьюринг в своей «игре в имитацию». Как это называется? Это называется позитивизмом, когда решение действительной проблемы объявляется «слишком неосмысленным», а затем действительная проблема подменяется «наблюдаемой», той, в отношении которой можно провести эксперимент, наблюдение. Вот подобное и громил Ленин в своей знаменитой работе «Материализм и эмпириокритицизм».

В статье Тьюринг много места отводит возражениям, которые можно выдвинуть против его идеи. Мы их здесь разбирать не будем, ни сами эти возражения, ни ответ на них со стороны Тьюринга ничего не прибавляют к описанию машины и мышления, данному выше. Отметим только, что среди этих возражений нет ничего диалектического и никаких отсылок к тому, что человек, в отличие от машины, существо общественное, что мышление — продукт общественного развития. Отказавшись от вопроса о мышлении машины, Тьюринг подменил его «игрой в имитацию», а затем на дело истории оставил проверку своей «игры». Попутно Тьюринг еще упомянул об обучающихся машинах, что станет популярным в 50-ые и 60-ые. Однако и это не относится к главному, что сделал Тьюринг — заменил действительный вопрос на его позитивистский вариант. В любом случае это показывает, чем были машины, с которыми сравнивали человека, и к чему стремились ученые, последовавшие за Тьюрингом, а последовали за ним все.

Мы видели предпосылки появления ЭВМ, теории, что мозг — это машина. Однако ЭВМ явно не дотягивала до человека, нужно было понять почему. Так появляется два направления. Одни полагали, что нужно взять что-то элементарное в мозге человека, а затем заставить это элементарное обучаться. Нейроны Мак-Каллока и были таким «элементарным» элементом мозга, идею же подсадить обучение в этот нейрон разовьет уже Розенблат. Другое направление полагало, что нужно просто перенести в ЭВМ все те знания, которые накопило человечество. Это направление постарается воспроизвести в ЭВМ те способности, которыми наделен человек — распознавать изображение, разговаривать.

До начала 70-ых ученые были полны оптимизма. Именно в этой работе Тьюринг предлагает «игру в имитацию». То, как Тьюринг предлагает отличить человека от машины, по формально заданным и полученным ответам, много говорит о том, как видел Тьюринг мир. Но и о мире, который не просто принял эту игру, но и вполне серьезно ее обсуждал, это говорит не меньше. Построения Тьюринга легко разбивались пониманием человека через труд, взаимодействие с миром, то есть понимание диалектическое, марксистское. Но ведь ученые Запада не были ни марксистами, ни диалектиками. Поэтому, например, они с удивлением и только в 60-ых узнают, что значение слов определяется их применением в практике человека. Из этого разовьется целое «научное» направление (Куайн). Только через такое полное отстранение от диалектики и марксизм можно понять и появившийся чуть позже аргумент Серля против Тьюринга. Спор, который в принципе не мог возникнуть при действительно научном подходе к миру, вполне серьезно продолжался и финансировался.

Здесь еще важно, что сама уверенность в том, что можно создать из 0 и 1 интеллект уровня человеческого никуда не исчезла, а только получила подпитку от идей Тьюринга. Благодаря успехам ЭВМ, а также укреплявшейся вере в способность ЭВМ подменить человека, в глазах ученых мир становился все более дискретным — считали, что мозг воспринимает мир дискретно, сам мир был дискретным. Возьмем такой аналоговый прибор как линейку. Мы можем измерить линейкой только длину. Однако если мы превратим весь мир в 0 и 1, а нашей линейкой будет что-то цифровое, то есть работающее с 0 и 1, то мы сможем измерить весь мир. Этими позитивистскими идеями и была полна философия, наука.

В те же 50-ые появляются статьи о машинах, играющих в шахматы, да и сами машины. Поскольку игры должны же свидетельствовать об уме, постольку попытки научить машины играть считались приближением к созданию электронного интеллекта. В это же время начинают заниматься машинным переводом. Опять-таки, раз отличительной чертой человека является язык, то не приблизит ли создание ИИ обучение машины языку? Или решение задач? Ньюэлл, Саймон начинают разработку эвристического подхода. Машина может перебрать все варианты и найти решение, но это слишком долго, да и может быть невозможным. Вот тогда пригодятся эвристики. Можно подсмотреть как человек решает задачки, не всегда следуя строгим правилам, а затем научить этим правилам машину. В 1957 появляется «Общий решатель задач» (GPS), а за этим направлением постепенно закрепляется название «искусственный интеллект». В 1956 начинают использовать термин «искусственный интеллект» по названию семинара в Дартсмутском колледже США, в а 1959 — машинное обучение.

Алгоритмический подход разрабатывали Ньюэл, Самймон. Это привело к эвристическому программированию. Однако и этот подход потерпел провал. Надо понимать, что значит провал. В рамках каждого были достижения. Но ни один подход не вел к созданию интеллекта, мышления, мозга как у человека. От широких задумок отказались, сосредоточились на доказательстве теорем, играм типа шахмат, решении задач с помощью ЭВМ (метод резольвенций Робинсона, программа STRIPS, теория поиска решений). К 1975 это направление тоже утратило былой оптимизм, так как программы становились все более сложными, громоздкими. Потребовалась автоматизация программирования, появился язык PLANNER. Ученые сосредотачиваются, например, на имитации общения (Виноград), распознавании образов. Задача прямого моделирования человека уже не ставится.

Возьмем книгу 1975 года «Искусственный интеллект» от автора Э. Хант и посмотрим, как он описывает развитие идей ИИ.

Автор начинает с того, что относится к области искусственного интеллекта. Для этого он берет образовательную программу курса «Искусственный интеллект». В курс входят: «доказательство теорем, игры, распознавание образов, решение задач, адаптивное программирование, принятие решений, сочинение музыки вычислительной машиной, обучающиеся сети, обработка данных на естественном языке, а также вербальное и концептуальное обучение».

Исследования по ИИ начались именно с написание программ для решения задач. Этим занимались Аллен Ньюэлл, Герберт Саймон и Дж. Шоу на базе корпорации РЭНД и Технологического института Карнеги. Решение задач означает, что есть некое текущее состояние, целевое состояние, а также операции, которые переводят систему из текущего состояния в целевое.

Ньюэлл с командой в 1957 создали программу Логик-Теоретик. Эта программа должна была доказывать теоремы из книги Уайтхеда и Рассела «Принципы математики». Программа изначально доказала 38 из 52 теорем, а затем, по мере развития ЭВМ, сумела доказать и все 52 теоремы.

К доказательству теорем возможно два подхода. Можно взять изначально верные утверждения, соединять их, смотреть выводы. Если собрать все возможные комбинации утверждений, то какой-либо вывод из них окажется искомой теоремой. Это алгоритмический подход, но он требует слишком много усилий. Его назвали алгоритмом Британского музея — посадите за пишущие машинки обезьян, со временем они напишут все книги, находящиеся в Британском музеи.

Противоположный подход основан на идеях Пойа, который считал, что алгоритмический подход нужно заменить эвристическим. Вместо поиска алгоритма нужно выдвинуть догадку о правильном решении, а затем ее проверить. Ньюэлл и команда использовали в своей программе именно эвристический подход.

Параллельно команде на базе РЭНД — Карнеги стала действовать команда из Массачусетского технологического института под руководством Марвина Минского и Джона Мак-Карти. Чуть позже образовалась еще одна группа — в Стэнфордском университете.

Наряду с решением задач, которые очевидно связаны с мышлением человека, стала разрабатываться такая отрасль как распознавание образов. Способность классифицировать образы считали основой мышления человека. Эта идея стала популярной в конце 50-ых. Для решения задачи классификации стали использовать теорию нейронов мозга. Здесь и пригодилась теория Мак-Каллока и Питтса (1943). Главной проблемой теории нейронов была необходимость обучать нейроны, чтобы они могли определять связи для произвольных объектов. Первоначально Хебб в 1948, а затем Розенблатт в 1958 развили идею перцептрона для распознавания образов.

Дальше автор переходит к вопросу вычислимости функций. В самом деле, работа ЭВМ — это вычисление. Если мы пытаемся создать из ЭВМ интеллект, то стоит задаться вопросом, что такое вычисление, как его поднять до уровня интеллекта, как оно может имитировать этот самый интеллект. Вопрос же вычислимости функций сводится к вопросу о вычислимости функции машиной Тьюринга. Вот что пишет автор: «Машина Тьюринга — это автомат, располагающий всеми логическими возможностями, которыми только может обладать реальная вычислительная машина. Поэтому принятое определение вычислимой функции связано лишь с возможностью вычисления ее машиной Тьюринга». Машина же Тьюринга, как это и было доказано Тьюринга, может вычислить все, что вообще вычислимо.

Мы пропустим подробное описание автором теории распознавания образов, чтобы перейти сразу к перцептронам. Развил теорию персептрона Фрэнк Розенблатт из Корнеллской лаборатории аэронавтики. Идея была такой. Пусть дан объект. Для этого объекта вычисляются некоторые функции, которые затем передаются как аргументы другой функции. Эта последняя выдает взвешенную сумму значений предыдущих функций. Сумма сравнивается с установленным порогом. Достигает сумма порога или нет — это и есть основа для классификации объекта. Особенностью такого персептрона была возможность «обучаться».

В более подробном изложении это выглядит так. Вход для персептрона называется сетчаткой R. Такой вход можно представить как набор иксов, у каждого из которых есть свой порядковый номер — индекс. Каждый из иксов принимает значение либо 0, либо 1. Вот запись для конкретного изображения X на сетчатке R:

X = (x₁, x₂, x₃, …, xᵢ, …, x {ⱼ}, …, xᵣ).

Далее есть предикаты, которые из всего множества точек изображения позволяют сделать вывод относится ли изображение к одному из классов. Перцептрон же это как раз «устройство», которое может определять предикаты, то есть может по заданному набору «точек» установить, к какому классу относится изображение, то есть к 0 или к 1.

В этом месте оставим книгу Ханта и возьмем книгу самого Розенблатта. Еще раз напомним, как представляли работу мозга передовые ученые того времени.

Мышление — это мозг, а мозг — это нейроны. Для нейронов же действует принцип «все или ничего», то есть действует бинарный принцип. Раз так, то можно применить математическую логику. В итоге можно построить логические сети, которые эквивалентны нейронным сетям, которые, в свою очередь, эквиваленты каким-либо свойствам мозга. Это были идеи Мак-Каллока и Питса (1943).

Эта идея предполагала однозначный вывод из данных посылок, так как речь шла о строгом следовании схеме. Идея Розенблатта была в другом, он предлагал применять вероятность. Вместо логических схем он предложил схемы, которые действуют на основании статистических принципов. Книга «Принципы нейродинамики» как раз и описывает такой подход. Суть такова. Можно задать «беспорядочные» сети, которые описывают реальность. Далее нужно подобрать сеть, которая с наибольшей вероятностью правильно описывает реальность. Математическое описание, данное Розенблаттом, было основано на «Теории матриц» Гантмахера и «Введении в теорию вероятностей и ее приложения» Феллера.

Как видел Розенблатт свою задачу? «По мнению автора, программа по исследованию перцептрона связана главным образом не с изобретением устройств, обладающих „искусственным интеллектом“, а с изучением физических структур и нейродинамических принципов, которые лежат в основе „естественного интеллекта“». Перцептрон для Розенблатта — это модель мозга. Причем Розенблатт вроде как осознавал ограниченность этой модели. Однако, как и любой позитивист, он ссылается на то, что такую модель можно хотя бы анализировать, а этого достаточно.

Исследования, по которым написана книга, проводились в Корнельском университете за счет Отдела информационных систем Управления военно-морских исследований.

Что понимается под моделью мозга? «Под „моделью мозга“ мы будем понимать любую теоретическую систему, которая стремится объяснить физиологические функции мозга с помощью известных законов физики и математики, а также известных фактов нейроанатомии и нейрофизиологии.» Перцептрон и есть такая модель мозга. Впервые автор предложил ее в 1957. Важность перцептрона в том, что он может показать, пускай на элементарном уровне, как приобретаются «знания», а также может делиться этими «знаниями». Сама идея перцептрона возникла изначально при изучении того, как работает память. Затем эта идея была расширена не только на запоминание, но и на восприятие.

Вот как Розенблатт в простой форме описывает перцептрон: «Перцептрон состоит из некоторого множества элементов, генерирующих сигналы («нейронов»), связанных в единую сеть. Каждый из этих элементов при получении соответствующего входного сигнала (поступающего либо из окружающей среды, либо от других элементов сети) генерирует выходной сигнал, который через соединительные связи может быть передан в заданное множество принимающих элементов.

Каждый перцептрон имеет сенсорный вход (т. е. некоторое множество элементов, способных реагировать на сигналы, поступающие из окружающей среды) и один или более выходных элементов, генерирующих сигналы, за которыми может наблюдать либо сам экспериментатор, либо какая-то автоматическая система.

Логические свойства перцептрона определяются:

— его топологической структурой, т. е. связями между элементами, генерирующими сигналы;

— набором функций распространения сигналов, или алгоритмов, управляющих генерацией и передачей сигналов;

— набором функций памяти, или алгоритмов преобразования свойств сети в результате активности.»

В чем отличие этой модели мозга от других? «В отличие от ряда других моделей мозга, или „нервных сетей“, перцептрон обычно характеризуется тем, что в нем допускается бóльшая свобода установления связей и что его поведение определяется не заранее заданными логическими алгоритмами, а постепенно создающимся смещением характеристик в нужную сторону.»

На каких идеях основывается Розенблатт? «Поскольку излагаемая здесь теория опирается на то же наследие философии, психологии, физиологии и техники последних столетий, что и другие современные теории, между ними неизбежно проявляется некоторое сходство в точках зрения и исходных положениях. В этом отношении автор отнюдь не претендует на оригинальность. В частности, используемая нейронная модель непосредственно восходит к модели, впервые предложенной Маккаллоком и Питтсом; основная философская концепция сформировалась под сильным влиянием теорий Хебба и Хейка и экспериментальных данных Лешли; особое пристрастие, которое автор питает к вероятностному методу, было не чуждым и другим теоретикам, таким, как Эшби, Аттли, Минский, Маккей и фон Нейман.»

Розенблатт указывает, что два положения являются общими для разных теорий мозга. Первое состоит в том, что свойства мозга определяются структурой сети нейронов, а также «динамикой распространения импульсов в этой сети». Второе же утверждает, что свойства нейронов можно «моделировать с помощью уже существующих электронных устройств». При этом он утверждает, что память, самосознание, разум являются только результатом «организации и функционирования нервной системы в целом». И как общий вывод: «Поэтому для того, чтобы понять, как работает мозг, необходимо исследовать, к каким последствиям приводит соединение простых нервных элементов в организованные структуры, топологически сходные с мозгом. Мы будем заниматься общим классом таких систем, одним из частных случаев которых является мозг.»

Отличие же подходов состоит вот в чем: «С одной стороны, имеется точка зрения, согласно которой мозг работает по заранее заданным алгоритмам, близким к алгоритмам, применяемым в цифровых машинах; с другой же стороны, высказывается мнение, что мозг функционирует не на основе детерминированных алгоритмов и функции его мало сходны с известными логическими и математическими алгоритмами, вводимыми в цифровые машины. Сторонники этой второй концепции (к которым принадлежит и автор) утверждают, что прежде чем можно будет построить теорию, адекватно описывающую механизмы мозга, должны быть найдены новые фундаментальные принципы. При этом утверждается, что для этой цели наиболее существенными являются вероятностные методы и механизмы адаптации.» Первый тип Розенблатт называет монотипным, а второй — генотипным. После такого деления он прослеживает историю этих подходов.

Начала монотипного подхода заложил Тьюринг своей работой «О вычислимых числах» (1936). Развитие его идей привело к созданию теории «универсальных автоматов». Смысл был тот, что «входящие» данные приводились к некой нормальной форме, а дальше сравнивались с заранее заданной моделью. Делалось это с помощью переключающих устройств, реле, что совпадало с идей нейронов. На этой основе Мак-Каллок и Питтс построили свою теорию в 1943. Вот как описывает эту теорию Розенблатт: «основополагающий принцип теории Маккаллока — Питтса заключается в том, что все психологические явления могут быть проанализированы и поняты как некоторая активность в сети, состоящей из логических элементов, принимающих только два состояния („все или ничего“). Полное описание такой сети и ее логики, по словам авторов, „дало бы все, что может быть достигнуто“ в области психологии, „даже если анализ дошел бы до конечных психических единиц, или „психонов“, ибо психон не может быть ничем меньшим, чем активностью отдельного нейрона… Закон „все или ничего“ этой активности и соответствие ее соотношений соотношениям логики предложений обеспечивают то, что соотношения психонов суть соотношения двузначной логики предложений“».

Генотипный подход отличается от монотипного: «При монотипном подходе свойства образующих нервную сеть элементов — нейронов — полностью заданы аксиоматически, так же как и топология сетей. При генотипном подходе свойства элементов также могут быть полностью заданы, но структура сети определена лишь частично в результате наложенных ограничений и задания функции распределения вероятностей, что приводит к заданию класса систем, а не какой-либо конкретной схемы. Таким образом, генотипный подход имеет дело со свойствами систем, подчиняющихся заданным законам организации, а не с некоторой логической функцией, осуществляемой конкретной системой.

Различие в методах приводит к существенным различиям в типах создаваемых моделей, а также в свойствах объектов, которые можно с их помощью моделировать. Для анализа характеристик монотипной модели, например, мало пригодна теория вероятностей; здесь используется исчисление высказываний, поскольку рассматривается отдельная полностью детерминированная система, которая либо удовлетворяет, либо не удовлетворяет требуемым функциональным уравнениям. С другой стороны, для генотипных моделей символическая логика может оказаться слишком громоздкой или даже совсем неприменимой (хотя в принципе любая конкретная система может быть представлена с помощью множества логических высказываний). При анализе таких моделей основной интерес представляют свойства класса систем, структура которых определяется введенными алгоритмами. Такие свойства лучше всего описываются статистически. Поэтому при этом подходе преимущественную роль играет теория вероятностей.

Второе существенное отличие заключается в методе определения функциональных характеристик модели. При монотипном подходе функциональные свойства обычно постулируются в качестве исходных данных. При генотипном подходе они выступают в качестве конечной цели анализа, а исходной является сама физическая система (или статистические свойства класса систем). Это означает, что здесь нет необходимости, до того как строить модель, предварительно во всех подробностях определять психологические функции; скорее следует надеяться на то, что генотипные модели помогут найти ответы на вопросы психологии, которые до сих пор остаются открытыми.»

Если монотипная модель развивалась под влиянием развития вычислительной техники и теории автоматического регулирования, то генотипная в большей степени зависела от физиологии и анатомии.

Розенблатт следовал за Хеббом и Хейком, а те — за Дж. Стюартом Миллем и Гельмгольцем. Еще интересно: «Интересно отметить, что одна из первых попыток применить теорию вероятностей к моделированию мозга была предпринята Ландалом, Маккаллоком и Питтсом в статье, появившейся в 1943 г. одновременно с моделью Маккаллока и Питтса, основанной на символической логике. В этой работе топология сети по-прежнему предполагается строго детерминированной, организация полностью известной, но при этом принимается, что, хотя импульсы и передаются с известной частотой, момент их появления неопределенный. Была высказана теорема, согласно которой для определения ожидаемой частоты реакции различных клеток можно использовать логические уравнения сети. Такой статистический подход непосредственно связан с работой фон Неймана по вероятности ошибок в сетях с ненадежными элементами.»

Далее Розенблатт излагает, как современная ему наука видит мозг. Остановимся только на этой цитате: «Автору настоящей работы кажется, что вопрос о „природе сознания“ можно обойти так же, как мы обходим вопрос о „природе восприятия“, концентрируя вместо этого внимание на экспериментальных и психологических критериях, позволяющих выявить подлинную сущность явлений. Когда испытуемый сообщает, что он „сознает“ или что он недавно находился в „бессознательном“ состоянии, мы можем поверить или не поверить ему в зависимости от его поведения и исходя из того, что́ он может рассказать о своем собственном „опыте“ в интересующий нас момент. С функциональной точки зрения явление „сознания“ тесно связано с доступностью информации и влиянием, оказываемым ею на внешне проявляемое поведение. По существу, бессмысленно утверждать, что индивидуум „сознает“, пока не указано, что является объектом его сознания. Вопросы, которые здесь могут возникнуть при построении теоретической модели мозга (когда мы не можем произвольно задавать процессы в модели, аналогичные процессам, протекающим в человеческом мозге), сводятся к тому, что́ именно можно различать, „видеть“, „прослеживать“, запоминать при определенных конкретных условиях. Единственно, что мы можем утверждать, — это то, что система ведет себя так, как если бы она была сознательной. Вопрос же об истинном существовании сознания в такой системе предоставим на усмотрение метафизиков.»

Таковы были идеи Розенблатта, которые легли в основу современного подхода к ИИ. На этом можно бы и закончить историю оснований ИИ, который на современном этапе превратился в бесконечное количество «чатов», «агентов» и т. п. Однако проследим еще немного историю.

К 1970 в журналах США начинают появляться предсказания, что мы совсем близко до создания искусственного интеллекта. На экраны выходит фильм Кубрика. Одновременно в 1969 выходит книга Минского, Пейперта «Перцептроны», которая громит идеи Розенблатта. Считается, что с этого начинается «первая зима» ИИ, что так как в ближайшие годы сокращается финансирование из военного бюджета США разработок, связанных с ИИ.

Исследования в это время полностью не прекращаются. Однако искусственный интеллект все больше понимается как имитация способностей человека. На все это можно смотреть так, что машина решает отдельные задачи, подобно человеку. Здесь правда возникает другое ограничение. Машина ограничена размером памяти. Могла возникнуть надежда, что по ходу решения проблем с памятью, начнется и приближение ИИ к человеку. Собственно, сейчас мы и имеем такой подход.

К этому времени ранее деление на два направления в создании ИИ только укрепляется. Их стали называть по-разному: от «нейрокибернетики» и «кибернетике черного ящика», до «чистюль» и «грязнуль». Суть оставалась примерно одинаковой. Одни хотели повторить структуру мозга и заставить эту модель обучаться, а другие — просто повторить результаты интеллекта человека, причем неважно как это работало на самом деле (Минский, Ньюэлл, Саймон). Здесь был возможен и какой-то синтез идей. Если научить машину отдельным функциям интеллекта, то ведь их как-то надо организовать в целое. В конечном счете, мозг человека не просто смотрит, слышит, но как-то соединяет это в одну «картину мира». Поэтому хотели найти «метапроцедуры», которые как-то организуют результаты всех этих процедур в наш интеллект. Считалось, например, в 60-ых, что такой метапроцедурой является «целенаправленный поиск». Это не помогло. Тогда в 70-ых начали искать «системы, основанных на знаниях». Мол, можно решить любую задачу, если получить знания и формальные процедуры. Это привело к экспертным системам. К 80-ым возвращаются к идеям, что может все организовано в сети, как раз нейронные.

До 80-ых перерыв. В 1983 Япония начинает разработку ЭВМ 5-го поколения. Весна продлилась пару лет, затем опять начали все сворачивать.

Обучение нейронной сети требует оценивания результатов. Вычислительно это сложно, поэтому нужны были новые методы. Таким методом стала обратное распространение ошибки.

К 1990 основные концепции в ИИ были созданы, укрепились. С тех пор дело было только за техникой. Нужно было больше памяти, более мощные процессоры. Когда в этих вопросах продвинулись к 2010 все ранее накопленные достижения просто получили возможность для реализации. В итоге к 2020-ым мы получили то, что принято называть искусственный интеллект.

Раздел 2 Введение в Data Science. Подготовка данных

Data Science (DS) — это наука о данных. С данными работают и другие науки. Особенность DS в том, что здесь 1) обрабатывают большие данные, 2) не понимают процесс, который стоит за данными. Поэтому DS — это обработка больших данных с целью понять процесс, который стоит за этими данными, но только на основе количественных, вероятностных методов. В самом деле, будь в науках, к которым относятся данные, понимание этих данных, то и DS не понадобился бы.

Так как DS надо обрабатывать большие данные, причем математически, то используются компьютеры. Это означает, что DS вынуждено так обрабатывать данные, чтобы соответствовать всем ограничениям, налагаемым еще и программированием. «Еще», потому что большие данные плюс математика уже предъявляют свои требования. Итого получаем три главных фактора, которые стоят между специалистом по DS и пониманием данных: 1) большие данные, 2) математика, 3) программирование. Именно эти препятствия, которые одновременно и единственные методы DS, определят все особенности DS.

Во всех классических учебниках по DS вы получите примерно такой вводный план: собрать данные; подготовить данные для обработки; обработать данные статистикой. Это необходимо, чтобы попытаться понять данные. Если бы на этом этапе смогли понять те законы, по которым развиваются процессы, описанные данными, то это было бы последним шагом. Однако именно это невозможно. На этом этапе мы получаем только гипотезы о процессах, чтобы иметь возможность лучше использовать машинное обучение. Этот этап может быть и заключительным, если нам не нужно предсказывать данные; машинное обучение. На этом этапе на основании статистического понимания процессов мы пытаемся предсказать данные.

Это выглядит логично. Проблема только в том, что жизнь работает иначе. Вы не собираете данные, не очищаете их, надеясь получить знания. Вы сначала хотите получить знания, применяете какие-то методы, убеждаетесь, что для применения этих методов требуется очистка данных, а уж затем эту очистку данных и производите. Повторив это раз-другой вы убедитесь, что начинать стоит, возможно, именно с очистки данных. Однако, если раньше вы могли и не догадываться, зачем бороться с пропусками в данных, то теперь-то вы точно знаете, что наличие пропусков просто повредит применению тех способов, которые вам нужны.

Таким образом, здесь хорошо бы начать с линейной регрессии. Однако мы выберем все же более классическое начало, ведь абзацем выше более правильный подход был намечен. Теперь же сделаем вид, что на собственном опыте убедились — начинать надо со сбора и подготовки данных. Пусть так, теперь давайте наметим, что такое «обработка статистикой» и «машинное обучение».

Статистическая обработка нацелена на: группировку данных; описание групп (медиана, среднее и т.п.); описание взаимодействия между различными группами данных (корреляция и т.п.).

Машинное обучение нацелено на создание алгоритма, который позволит предсказывать целевой признак на основании заданных признаков в автоматизированном режиме. Другими словами, статистическая обработка позволяет понять процессы, а машинное обучение — предсказать процессы.

Однако начинается все с предварительной подготовки данных. Состав подготовки зависит от качества данных. Качество определяется тем видом, в котором пришли данные, а также полнотой данных. Данные могут быть в табличной форме, текстовой и т. п. Данные могут полностью описывать изучаемый процесс, содержать пропуски, неправильные данные и т. п. От всего этого зависит, как правильно подготовить данные. В этой книге мы будем заниматься табличными данными о книгах. Данные достаточно полные, в них нет пропусков, а определенные странности в данных, которые могут нам помешать, мы устраним.

В общем же случае подготовка данных включает в себя такие этапы: очистка имеющихся данных; понимание данных; дополнение данных.

Выше мы писали, что DS возникает для задач, для которых у нас нет понимания процессов, а в предыдущем абзаце пишем, что нужно понимать данные. Как же так? Так или иначе, но у нас есть картина мира, в которую вписываются или не очень данные, полученные нами. Так, например, мы не знаем точно закона, по которому люди ставят оценки книгам. Однако у нас есть представление как о процессе чтения книг, так и о процессе проставления оценок.

Универсальный перечень этапов подготовки данных дать нельзя, потому что слишком уж много разных недостатков может быть в данных. Однако вот примерный перечень, который будет полезен для обработки наших данных: проверка правильности формирования индекса, наименования столбцов (признаков). Например, может быть обнаружено, что в наименовании столбцов есть лишние пробелы; проверка типа данных. Например, численные данные могут быть отмечены как объекты или наоборот; поиск дубликатов; очистка строковых данных от лишних символов. Например, наличие слэша там, где это очевидно неуместно; обработка значений, которые, очевидно, являются ошибочными. Например, в столбце с количеством страниц указан жанр книги и т.п.; проверка на чистоту признаков. Нельзя смешивать категориальные данные и числовые в одном признаке.

Дополнение данных включает: создание новых признаков. Например, по значениям двух уже имеющихся столбцов можно создать третий; укрупнение категорий в категориальных признаках.

Перед тем, как мы начнем изучать наши данные, нужно сделать такое отступление. Приводить код мы не будем. Во-первых, этот код мы разместим на GitHub. Во-вторых, во времена, когда программировать помогает ИИ, большого смысла в нашем коде нет, так как он не содержит ничего специфичного.

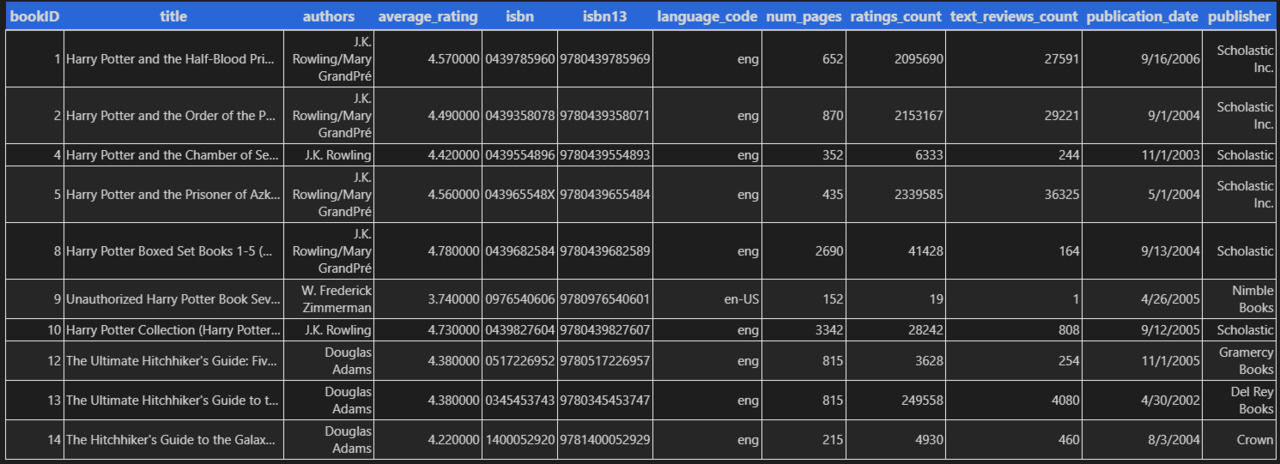
Живи мы в лучшем из миров, данные воспринимались бы как процесс, развитие. Тогда в таблице мы должны были бы увидеть не перечисление признаков, а процесс, описание процесса. О каком процессе идет речь в данных? Автор пишет книгу. Издательство издает книгу. Книга попадает читателю. Сайт, который предоставляет данные, имеет определенный функционал оценивания. Читатель оценивает книгу.

Однако нам пока так не повезло, с миром. В этой книге наша цель — показать, как DS устроен сейчас, и только чуть-чуть наметить, как же правильно, диалектически применять DS. Поэтому мы будем идти по классическому пути подготовки данных.

Разберем наши признаки по этапам этого процесса.

Автор пишет книгу: title; authors.

Книгу издают: isbn; isbn13; language_code; num_pages; publication_date; publisher.

Здесь важно отметить, что автор почти не влияет на конкретное количество страниц, язык, дату публикации, хотя может показаться иначе. Однако автор не может заранее предсказать, на какой язык его переведут, в каком формате издадут (от этого зависит количество страниц), в какой день выйдет его книга.

Книгу читают:

этот этап в данных пропущен. Что его могло бы характеризовать? Сколько дней книгу читают, делают ли заметки и прочее.

У сайта есть определенный функционал:

этот функционал представлен всем набором данных, сам набор и отражает такой функционал.

Книгу оценивают: average_rating; ratings_count; text_reviews_count.

Уже здесь мы видим, что выпадает bookID. Этот признак не имеет отношения к нашему процессу, он только служит для нумерации книг в таблице. Поэтому данный признак можно удалить.

Таким образом мы уже начали очистку данных. Выполним и другие виды очистки. Повторимся, что единого алгоритма подобной очистки данных нет. На что обратить внимание — это зависит от конкретного набора данных. Однако на практике часто встречаются со следующим: проверка названий столбцов; поиск дубликатов; проверка типов объектов; проверка дат; проверка на аномальные значения.

В названиях столбцов обнаруживается ' num_pages’, то есть лишний пробел. Исправим это. Вот как будет выглядеть список названий столбцов: ’title’, ’authors’, ’average_rating’, ’isbn’, ’isbn13», ’language_code’, ’num_pages’, ’ratings_count’, ’text_reviews_count’, ’publication_date’, ’publisher’.

Теперь мы будем искать дубликаты в данных.

Мы можем искать либо полные дубликаты, либо искать дубликаты выборочно. Здесь надо обратить внимание, что isbn является уникальным идентификатором каждой изданной книги. Поэтому логично искать дубликаты только по этому признаку, так как книги вполне могут совпадать по иным признакам и это нормально.

Давайте на минутку остановимся и задумаемся. isbn делают для каждого издания книги. У книги может быть один автор, название, количество страниц — во всем книга будет совпадать с прежним изданием. Однако это будут две разные книги с позиции isbn. Нам это нужно запомнить, потому что читатели ставят оценку не книги вообще, а конкретному изданию книги.

Исследование наше показывает, что дубликатов по isbn нет. Изучим типы объектов.

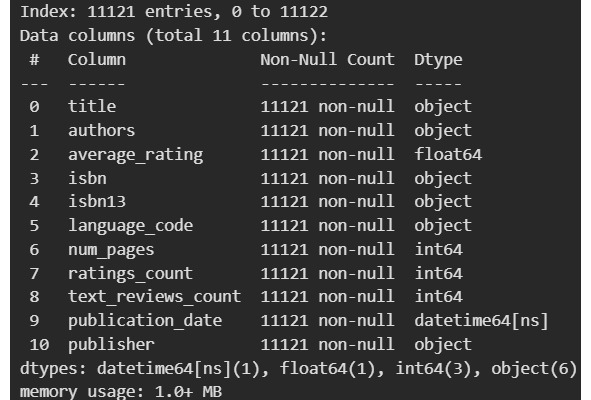
Видим, что есть 11 признаков (нумерация начинается с 0 и продолжается до 10) и 11123 наблюдений (позже их станет 11121, что и отражено на изображении). Пропусков нет (количество объектов по столбцам одинаковое). Индекс у нас это RangeIndex. По типам данных заметно две проблемы. isbn помечен как объект, а isbn13 как int64. Кроме того, publication_date помечен как объект, хотя это очевидно дата. Изменим тип данных.

В результате этого в publication_date появилось два пропущенных значения. Так как подобных строк всего две, можно их удалить.

Теперь нам надо искать аномалии в данных. Для этого возьмем стандартное описание данных.

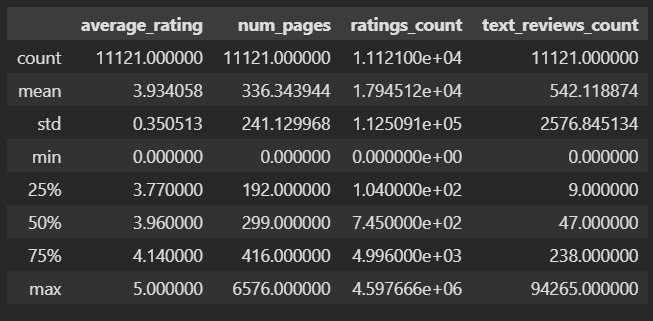
Мы видим, что минимальное количество страниц — это 0. Нам важно, чтобы книги были книгами. По тем данным, которые у нас есть, это можно определить только на основании количества страниц. Если у книги нет страниц, то это не книга или не бумажная книга. Поэтому мы удалим такие «книги» из набора.

Кроме того, предполагая, что могут быть издательства, издающие только аудио книги, мы удалим и их, предварительно оценив их количество. После выполнения кода получим такой результат: книг с нулевым количеством страниц — 76; книг от издательств аудиокниг — 181; фактически удалено строк — 211; текущий размер датасета: 10910.

Нас не интересуют ситуации, когда у книги нулевой рейтинг. Поэтому посмотрим, сколько таких значений, а затем удалим их: книг с нулевым рейтингом — 25; фактически удалено строк — 25; текущий размер датасета — 10885.

Теперь стоит обдумать наши данные. Мы видим данные как процесс, а не как набор признаков: автор пишет книгу, издательство издает… Мы осознали, что издательство может одну и ту же книгу издавать несколько раз под разными isbn.

Добавлять нужно те признаки, которые еще сильнее превращают данные в историю, а также показывают изменение данных. Издания под разными isbn могут отражать разные годы, даже десятилетия издания. Это может отражать изменение предпочтений читателей. Мы знаем, что оценки ставить на сайте стало можно с нулевых, а книги могут быть изданы и раньше. Кроме того, читатели могут оценивать не конкретное издание, которое они прочитали, а то издание, которое выпало по названию. Как все это учесть?

Здесь мы вспоминаем, что именно специалист по DS заставляет данные двигаться, наполняет их историей. Это невозможно без определенной гипотезы о данных. Нашими гипотезами будут такие: 1) читатели ставят оценки не конкретном изданию, а книге; 2) читатели ставят оценки не переводу, если он есть, а книге. Наличие перевода мы определяем по наличию второго автора после слэша.

Для реализации этой гипотезы, мы в колонке автора уберем слэш и второго автора. После этого мы удалим те дубли, у которых меньше оценок. Мы также добавим указание на то, что у книги были другие издания, их количество. Указание же на издательство мы уберем. Год издания мы оставим, чтобы изучать, например, классические произведения.

Теперь мы введем еще одну гипотезу. Мы оставим из даты только год и квартал. Квартал, в который издают книги, играет важную роль в издательском бизнесе, популярные книги ставят в один месяц, непопулярные в другой.

Посмотрим же, что получилось из нашей таблицы после преобразований.

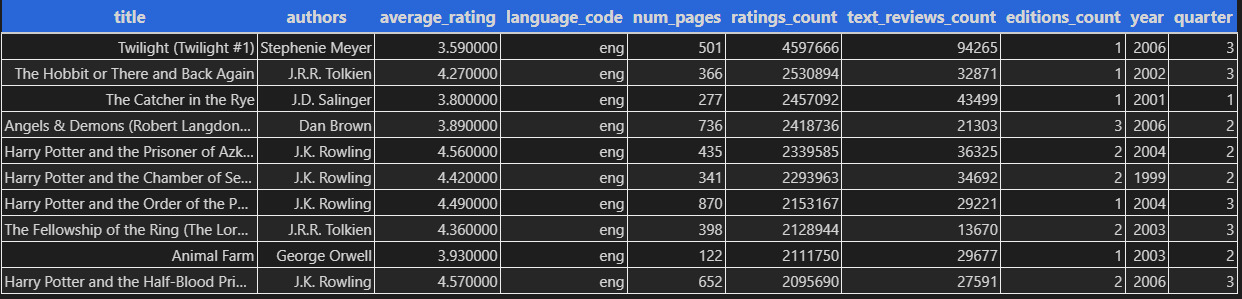
Нам нужно найти развитие в данных. Машина этого не может. Мы можем, но как искать? Искать А, искать В? Часто проще найти противоречие. Где противоречие, там и развитие. Мы решаем две задачи: 1) понять данные, 2) предсказать данные. Понимать мы будем весь набор, предсказывать — оценку от читателей.

Для понимания всей таблицы нам надо определить, а что является той клеточкой, из которой вырастают эти данные? Это неясно пока. Обычно ищут исторически. Из чего зарождается тот процесс, который мы наблюдаем в данных. Не из производства книги, хотя без него нельзя. Зарождение происходит в момент столкновения книги и читателя. Но где это в данных? Эту таблицу порождает чтение. Но что говорит нам о чтении? Только язык и количество страниц.

К полученным данным нужно еще несколько замечаний.

С 2007 возможность оценки появилась. Поэтому до 2007 мы имеем ретроспективные оценки, а после — по мере органического роста продаж.

В издательском бизнесе самые прибыльные периоды — осень. Так, например, в Великобритании издатели стараются издать главные книги в начале октября, чтобы книги добрались до магазинов к покупке рождественских подарков. В мае и июне стараются издавать легкие детективы, триллеры, любовные романы, то есть то, что можно почитать в отпуске. В январе издают бизнес-литературу, книги по саморазвитию, диетам. В августе книги издаются мало. В США процессы аналогичные. Книги стараются издать в сентябре-середине ноября. Это время для серьезной литературы, которая может претендовать на престижные премии.

Количество страниц в книге определяется технологией печати. Книги печатают на больших листах, которые затем складываются и разрезаются. Учитывая, что эти листы затем склеиваются, то оптимальным считается объем в 300 страниц. Книги на 400 и более страниц требуют другого, более дорогого переплета.

Коснёмся вопроса о разведочном анализе данных — ведущем направлении в Data Science на Западе. Это направление, которое начал разрабатывать Джон Тьюки в 70-ые, стремится оценить данные «по-быстренькому». Поэтому основывается она на визуализации, графиках. Никто не запретит такой подход. Графики вполне могут оказаться полезными, однако упор на них делать не нужно. Наоборот, упор на графики подчеркивает стремление формализовать данные, процессы, которые этими данными описываются. Вместо того, чтобы понять данные, мы хотим их описать так, чтобы они, эти данные, нам что-то сказали этим своим формальным описанием.

Пускай наш мир даже состоит из объектов, а не из процессов. Или представим, что в понятие объекта мы включили и процессы. Объекты имеют качественные и количественные характеристики. Это не две разные категории, они взаимосвязаны. Качество описывается количеством, количество — это количество конкретного качества.

Данные в нашей таблице говорят о качестве — страницы, издательства, но о качестве, имеющем определенное количество — 300 страниц. Одни данные останавливаются только на качестве — такие данные называют категориальными, другие говорят о количестве — такие данные и называют количественными. Данные могут быть и порядковыми, то есть выражены в числах, но без значения количества. Собственно рейтинг книги — это количественное описание качества или порядковые данные?

В зависимости от типа данных, их количества выбирают и тип графика. Для одного количественного признака хорошо подходит гистограмма. Для двух количественных признаков можно взять диаграмму рассеяния. Качественные признаки можно исследовать с помощью столбчатых диаграмм.

Раздел 3 Статистическая обработка

У статистики две задачи: 1) объяснить имеющиеся данные; 2) спрогнозировать по новым данным события.

Кажется, что эти задачи решает любая наука, зачем же нужна статистика? В первой главе мы писали, что DS решает задачу понимания данных и предсказание событий там, где у других наук нет никаких представлений о процессах, которые стоят за данными. Но DS только развитие статистики. Поэтому-то в основе своей статистика и DS вполне совпадают.

Итак, статистика берется объяснить то, что не может объяснить наука. Как же это удается? Ниже мы поговорим об основных концепциях статистики. Из этого станет понятным, что статистика справляется со своей задачей за счет предположения, что в этом мире случается лишь то, что имеет большую вероятность.

Статистика может работать с разными наборами данных, но мы будем работать в этой книге с таблицей. В первой главе мы уже видели таблицу, теперь давайте получим из того конкретного образа абстрактный.

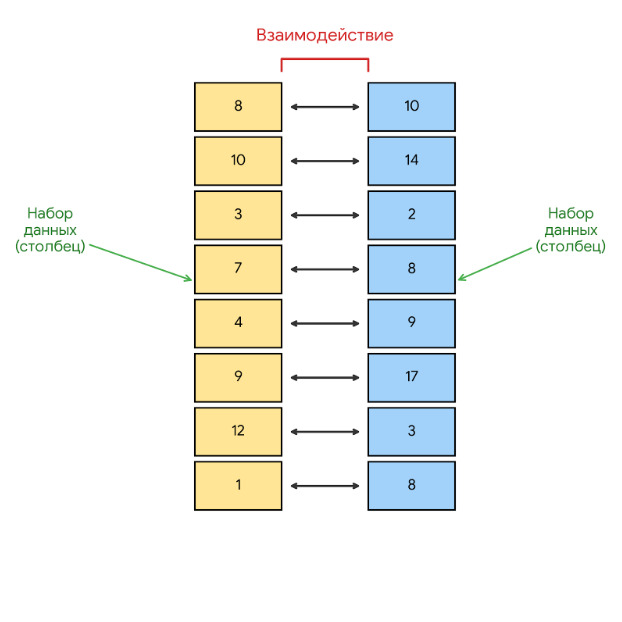
Если смотреть на это как на таблицу, то столбцы — это столбцы чисел, ничего особенного. Если же полагать, что таблица наша отражает реальный процесс, то столбцы эти — признаки какого-то процесса. Например, в нашей таблице с оценками книг, столбцы отражают признаки книг (количество страниц), признаки отношения читателей к книгам (количество оценок, количество обзоров).

Какие вопросы можно задать, глядя на этот рисунок? Например, можно заинтересовать только одним из столбцов. Какое среднее значение? А как отличаются от среднего фактические значения? Насколько вероятно появление одного из значений или нового значения? Может заинтересовать и взаимодействие столбцов. Если растет значение в одном столбце, то растет ли значение в другом? Связаны ли эти столбцы? И если связаны, то насколько сильно? И вот еще что важно. Данные, которые мы здесь используем, — это только небольшая выборка всех книг, изданных в мире. Поэтому те данные, которые видны выше на рисунке, — это тоже только выборка из всего объема данных по книгам, которую называют генеральной совокупностью. А раз так, то стоит задача оценить по этим выборочным данным генеральную совокупность (или же наоборот, если известны характеристики генеральной совокупности).

Все это можно сделать со столбцами. И статистика как раз пытается ответить на вопросы выше. Итак, статистика: дает математическое описание набора данных (столбца); определяет вид распределения (для определения вероятности новых значений и не только); дает описание того, как взаимодействуют два и более набора данных (столбцы).

Хорошо, а как же статистика пытается ответить на эти вопросы? Рассмотрим некоторые основные понятия статистики.

Если нам дан набор чисел, то мы можем заметить, что в нем некоторые числа повторяются. Это может натолкнуть нас на мысль, что даже если в наборе каждое число появляется один раз, это все-таки говорит о частоте чисел в наборе. Так постепенно возникает идея подсчитать математическое ожидание чисел. Для этого достаточно взять каждое число из набора и умножить его на вероятность появления в наборе, а затем все такие произведения сложить. Математическое ожидание примерно равно среднему значению. Причем математическое ожидание тем ближе к среднему, чем больше у нас наблюдений. Поэтому чем больше данных, тем лучше.

Итак, мы имеем набор чисел и математическое ожидание числа. Например, набором будет «1, 2, 3, 4, 5, 6», математическое ожидание мы получим, если возьмем каждое число и умножим на вероятность его (1/6 для каждого числа), а затем просуммируем произведения. Получим матожидание в 3,5. Что можно сделать с этим числом? Можно вычесть из чисел набора математическое ожидание. Так мы «центрируем» наши данные. Само же математическое ожидание принимается за центр распределения набора данных.

Теперь мы знаем математическое ожидание и поняли, что можно вычитать его из чисел нашего набора. Тогда мы можем посчитать дисперсию, то есть разброс наших данных от центра. Этот разброс называется дисперсией, которую можно записать так:

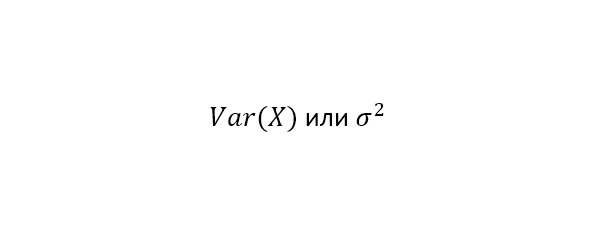
Для каждого числа в наборе берем разность с матожиданием, результат возводим в квадрат. После этого находим матожидание получившихся квадратов:

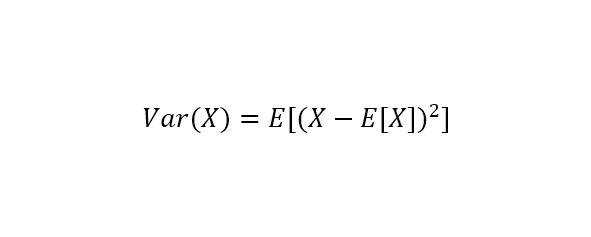
В этой записи надо учитывать, что прописная X означает весь набор данных, например 2, 4, 6. Матожиданием E [X] здесь будет (2+4+6) /3 = 4. Теперь вычтем из 2, 4, 6 наше матожидание 4, то есть сделаем вот это (X — E [X]) ^2. Получим новый набор чисел: 4, 0, 4. Матожидание же этого нового набора будет (4+0+4) /3 = 2,67.

Следующая важная для статистики концепция — это концепция начальных и центральных моментов. От центральных моментов нужно отличать понятие центрального положения, под которым понимают такое число, которое является наиболее «типичным» для набора чисел: среднее, медиана, мода. Почему центральное положение? Посмотрим на рисунок.

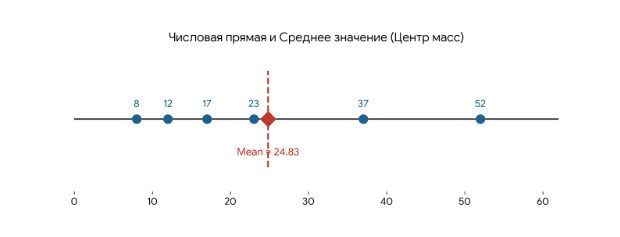
Среднее значение 24,8 есть характеристика центрального положения, так как фактические данные (8,12…52) расположены вокруг этого среднего. Отсюда же видно, например, что можно посчитать расстояние от центра до каждого значения, что приводит к дисперсии и стандартному отклонению.

Возвращаемся к центральным моментам. Опять берем набор чисел, для которых известна вероятность появления.

Для этого возьмем произвольный набор данных, в котором для каждого значения известна вероятность.

Вот как считается математическое ожидание:

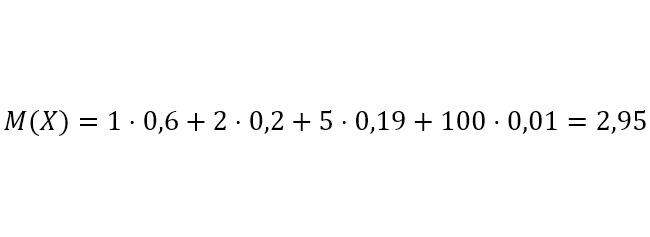
Еще раз, важно запомнить, что в записи M (X) вот это X означает случайную величину, скажем измерения линейкой. Отдельное значение из этой случайной величины (верхняя строка в таблице выше) обозначается как x. Когда же есть запись с X, то имеются ввиду все значения x.

Итак, теперь возведем в квадрат случайную величину.

Вероятность не изменилась. Это можно понять так. Возведением в квадрат изменяется масштаб, но не вероятность. Каким будет математическое ожидание?

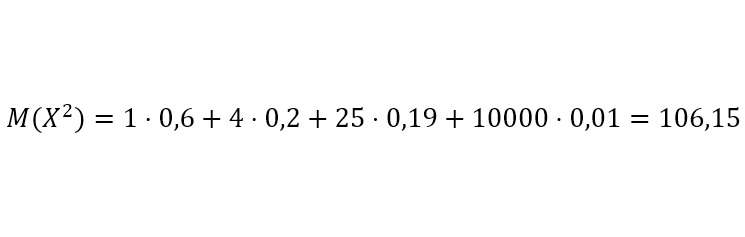
Какой вывод можно сделать? Второе математическое ожидание гораздо больше первого. Почему? Потому что в первом случае мы умножали вероятность 0,01 на 100, а во втором ту же вероятность 0,01 мы умножали уже на 10000. Это позволило учесть те значения, которые имеют маленькую вероятность. В зависимости от количества подобных величин, того, насколько они «маленькие», может потребоваться возведение не только в квадрат, но и в более высокие степени.

Не так строго понять это можно следующим образом. Сначала мы находим среднее значение набора данных (это будет математическим ожиданием). Затем вычитаем из каждого значения набора данных это среднее значение. Получается новый набор данных. Теперь можно найти среднее этого нового набора данных (это также будет математическим ожиданием, но для нового набора данных).

Теперь нужно разобраться с понятиями выборка и генеральная совокупность.

Выборка — это случайно отобранные из всего набора числа. Соответственно весь набор чисел называется генеральной совокупностью.

Понятия «выборка» и «генеральная совокупность» нам необходимо для того, чтобы применить концепцию распределения. Под распределением понимают отношение набора чисел в выборке, генеральной совокупности и вероятности таких чисел.

Данные по оценке книг, которые мы начали разбирать в первой главе, являются выборкой из генеральной совокупности (все оценки, поставленные всеми пользователями). Если представить график, то точки на графике — это наши числа, такие числа имеют вероятность «попадания» на график. От этой вероятности зависит, как будет выглядеть наш график. Такой вид графика и можно считать распределением. Раз речь про график, то есть какие-то параметры, которые определяют его построение, то есть та функция, по которой график построен. Например, для нормального распределения функция будет содержать математическое ожидание и среднее квадратическое отклонение, а для распределения Пуассона — параметр лямбда. Если подходить более формально, то под функцией распределения понимают такую функцию, которая показывает вероятность, что случайная величина из набора примет конкретное значение.

Посмотрим на нормальное распределение.

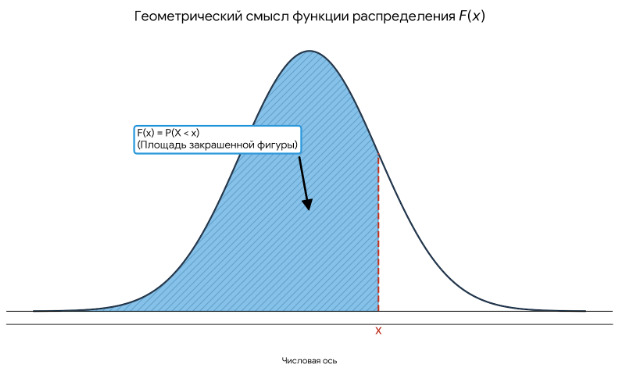
Функция распределения показывает, какая вероятность, что случайная величина будет иметь значение, лежащее левее x. На этом графике показана плотность распределения вероятности, а не конкретное значение такой вероятности. Конкретное значение вероятности можно получить по графику кумулятивной функции распределения (CDF).

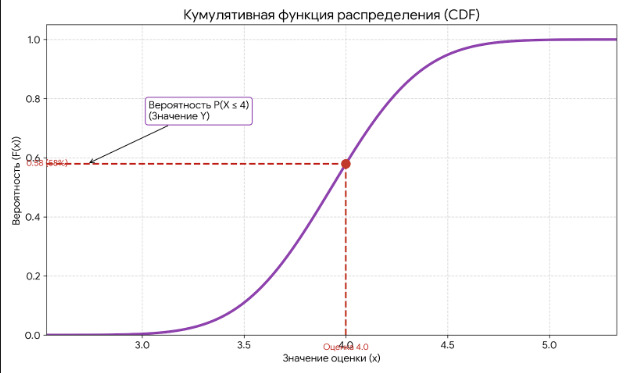
Как его правильно читать? Проведу из произвольной точки на оси x перпендикуляр. Точка пересечения перпендикуляра с графиком даст значение y — вероятность того, что произвольная точка примет значение равное или меньшее x. Например, берем оценку 4. Видим, что вероятность получить такую оценку между 0,5 и 0,6, примерно 58%.

Для примера возьмем наш набор данных об оценках книг. Параметр, который нас интересует, — это количество страниц. Количество страниц в каждой книге — это и есть количественный признак генеральной совокупности.

Мы можем брать одну, две, сколько захотим выборок из генеральной совокупности. Каждая выборка будет содержать набор чисел. Например, наши данные являются выборкой. Из всех данных о всех оцененных книгах можно получить несколько других выборок. В наших данных и в других выборках мы можем получить какой-то параметр, например среднее значение количества страниц в книгах. Для каждой выборки у нас получится свое среднее. Если взять среднее значение таких средних по выборкам, то это значение будет приближаться к истинному среднему генеральной совокупности.

Из этого получается понятие несмещенной оценки. Те параметры, которые мы получаем на данных выборки, называются статистической оценкой (среднее значение страниц в книгах, например). Если статистическая оценка на выборке равна статистической оценке генеральной совокупности, то эта оценка называется несмещенной. Например, среднее значение числа страниц в книгах на нашей выборке является несмещенной оценкой среднего числа страниц в книгах всех книг (генеральная совокупность). Если это правило не выполняется, то статистическая оценка называется смещенной.

Однако, даже если оценка является несмещенной, все-таки дисперсия оценки может быть большой. Поэтому еще одним требованием к оценке является эффективность. Эффективная оценка — это такая несмещённая оценка, дисперсия которой минимальна среди всех возможных несмещённых оценок. Например, если мы берём среднее число страниц в книгах, рассчитанное по большой выборке (например, всех 10 000 книг), то дисперсия этой оценки будет меньше, чем если бы мы рассчитывали среднее по небольшой подвыборке (например, 100 книг). Хотя обе оценки несмещённые, оценка по полной выборке считается более эффективной, поскольку её разброс при повторном извлечении выборок значительно меньше.

Теперь подробнее рассмотрим нормальное распределение. Вот его график:

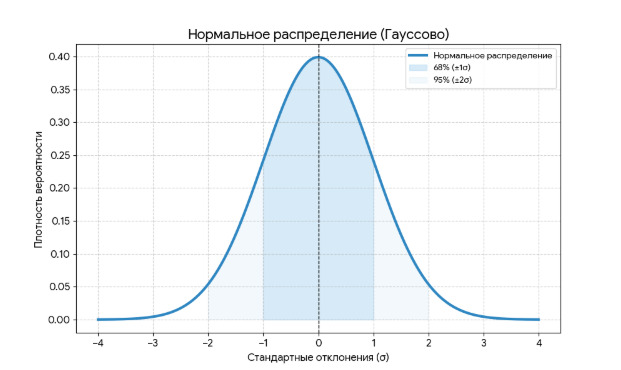
Нормальное распределение определяется двумя параметрами: математическим ожиданием (a) и средним квадратическим отклонением. Нужно помнить три правила:

1) если изменяется a, то форма графика не меняется, но «колокол» сдвигается: вправо, если a возрастает, и влево, если a убывает; 2) если среднее квадратичное отклонение увеличивается, то вершина «колокола» прижимается к оси x, если уменьшается, то вершина становится более остроконечной; 3) площадь под колоколом всегда равна 1.

В связи с нормальным распределением есть центральная предельная теорема (теорема Ляпунова). Смысл этой теоремы в том, что если каждое значение в наборе имеет малое влияние на весь набор, то весь набор таких чисел имеет нормальное распределение.

Стоит еще отметить разницу между дисперсией, ковариацией и корреляцией:

1) дисперсия — это мера изменчивости конкретного значения от среднего значения по всему набору данных; 2) ковариация — это мера взаимосвязи между изменчивостью двух переменных. Ковариация зависит от масштаба, поскольку она не стандартизирована; 3) корреляция — это связь между изменчивостью двух переменных. Корреляция стандартизирована, что делает ее не зависящей от масштаба.

Теперь вспомним наши данные по оценке книг и чуть улучшим наименование колонок.

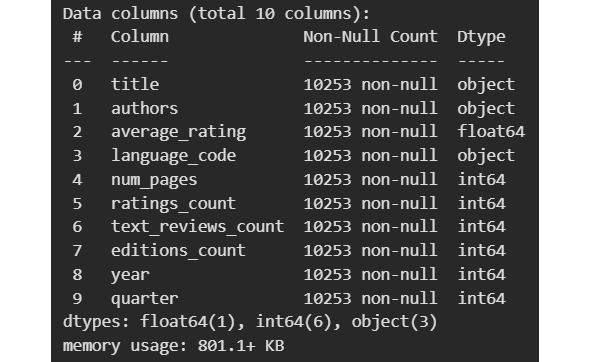
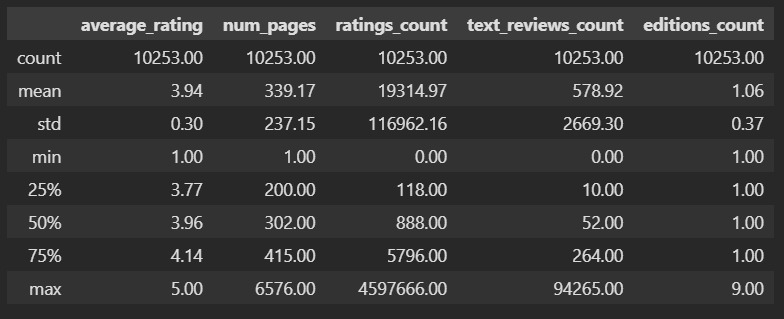
Это статистика для наших числовых данных. Ниже мы отдельно посмотрим статистику для категориальных данных.

В чем смысл таких характеристик? У нас есть набор данных, который мы хотим как-то охарактеризовать. Зачем? Во-первых, чтобы лучше понять объект, который описывается этими данными. Например, про среднюю оценку мы теперь знаем, что она у книг составляет 3.9. Во-вторых, чтобы уметь предсказывать будущие события. Например, мы хотим знать, а какую оценку поставят новой книге. При прочих равных можно считать, что эта оценка будет близка к среднему значению. Но так как точно сказать этого нельзя, то нас интересует, в каком диапазоне может быть эта оценка, здесь помогает std. Минимум и максимум определяют, в каких границах расположены оценки. Благодаря этому мы достоверно знаем, что оценка не может быть меньше 1 и не может быть больше 5. А к чему же все эти проценты: 25%, 50%, 75%? Эти проценты показывают следующее: 25% оценок ниже, чем 3.77, 50% оценок ниже, чем 3.96 и т. д. Это условно можно представить как вероятность: вероятность того, что оценка книги будет 3.77 составляет 25%.

Уже здесь мы видим, что книги, как правило, оценивают положительно. Средняя оценка почти 4 и всего 25% читателей ставят оценки ниже 4. Еще одна особенность состоит в том, что стандартное отклонение в 0,3 является незначительным. Такое незначительное варьирование данных может создать проблемы при предсказаниях оценки. Оценить такую волатильность можно по отношению к разбросу данных. Отклонение на 0,3 в наборе из чисел от 1 до 5, это не то же самое, что отклонение в 0,3 в наборе от 1 до 1000.

Любопытны сведения о количестве страниц. Среднее значение в 339, а вот стандартное отклонение 237, то есть размер книги может отличаться от среднего в среднем на 237. Аномальным выглядит количество страниц в 1 и 6576. Однако мы видим, что среднее в 339 страниц вполне соответствует стандарту в издательской отрасли, который зависит от особенностей печати книги.

В количество оценок колоссальная разница. При среднем в 19 тысяч отклонение составляет 117 тысяч. Аналогичная ситуация и с количеством обзоров. Все такие колоссальные «разницы» можно сглаживать логарифмированием и нормализацией. Вообще же такое большое значение стандартного отклонения означает, что книги более популярные получают больше отзывов и оценок.

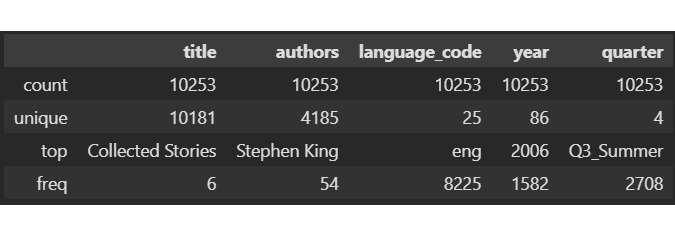
По категориальным данным нас здесь интересует язык — большинство книг написано на английском и в 2006. Самый популярный квартал третий, то есть летнее время. Год может говорить скорее, о том, как собирался набор данных. Любопытно, что уникальных авторов всего 4 тысячи на набор из 10 тысяч книг.

Оценить данные можно и с помощью визуализации данных. Это направление стало особенно популярным с 70-х годов 20 века. Однако визуализация, которая может быть полезна в отдельных ситуациях, точно не полезнее результатов специальных статистик, критериев, коэффициентов. Поэтому увлекаться визуализацией не стоит. Считается, что визуально человеку проще схватить «паттерны» в данных.

Визуально человеку проще это сделать. Однако надо помнить, что размещение слишком большого количества данных на графике уменьшает этот эффект простоты. Например, на одном графике можно точками отразить распределение по двум признакам, сюда же добавить третий признак цветом точек, четвертый — размером точек, пятый — их формой. Но такой график будет крайне сложно прочитать, а значит и смысл в визуализации теряется.

Однако давайте все же попробуем визуализировать наши данные. Здесь мы хотим установить следующее:

1) вид распределения целевого признака — средняя оценка; 2) наличие выбросов по количественным признакам; 3) наличие взаимосвязи между признаками; 4) соотношение категориальных данных там, где это уместно.

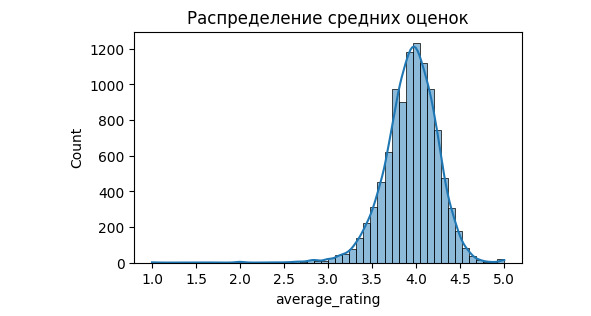
На этом графике ширина столбика показывает частичный интервал, а высота — количество значений в этом интервале. Возможно построить гистограмму, где высота столбика будет показывать плотность вероятности.

Гистограмма позволяет сделать предположение о виде распределения данных. Но зачем нам это? Вид распределения позволяет делать предсказания о вероятности того или иного события. Кроме того, для проведения статистических тестов, определения некоторых метрик требуется распределение определенного вида. Как правило, распределение должно быть нормальным. Если распределение нормальным не является, то данные можно привести к нормальному распределению или можно использовать специальные тесты, метрики. Поэтому важно ответить на вопрос: распределены ли данные нормально? Если нет, то нужно установить вид распределения.

Именно это позволяет статистике справляться со своей задачей. Напомним, что статистика должна дать понимание данных и предсказание будущих событий в ситуации, когда никакого понимания процесса, стоящего за этими данными, нет. Сделать же это можно через числовое описание данных, к которому затем будет предъявлено требование — должно соответствовать определенному распределению. И раз мы знаем распределение, то даже не зная закон, который к этому распределению привел, мы можем успокоиться на том, что такого понимания данных достаточно, к тому же такое понимание возможность предсказывать будущие события. Грубо говоря, пускай монетка в среднем выпадает орлом чаще, чем решкой. Это вполне возможно, если из-за особенностей сплава, формы, есть перевес в сторону «орла». Мы не знаем точно закон, по которому выпадает орел, но в среднем — выпадает именно орел. Мы тогда можем предсказать что и дальше в среднем будет выпадать орел. Заметьте, никакого знания о процессе нам не потребовалось.

Давайте еще раз посмотрим на наш график. Видно, что центр графика смещен к оценке 4, от единицы до 3 практически не ставят оценок. Объяснить это можно по-разному. Можно объяснить так, что книги «плохие» издают маленьким тиражом, они не доходят до читателя, а потому и оценку не получают. Но в рамках статистики и при тех данных, которые у нас есть, мы не можем сделать точный вывод о причинах такого распределения. Мы лишь фиксируем его.

Обсудим еще выбросы в данных.

Выброс — это такое значение, которое пришло не из того распределения, из которого пришли основные данные. В этом смысл того, чтобы определить распределение для большинства данных, а затем уже выброс. Редкие данные возможны и в границах распределения для основных данных, но вот выброс выходит вообще за границы распределения, то есть, например, за пределы колокола в нормальном распределении. В этом смысл того, что сначала надо найти отличающиеся от других данные, а затем проверить их на влиятельность.

Мы ищем выбросы, чтобы понять, есть ли они. Если есть, то нужно определить причину их появления. На этом основании нужно решить, что мы будем с ними делать, например можно удалить.

Искать выбросы можно визуально, а можно с помощью применения специальных тестов. Визуально ищем с помощью «ящика с усами». Для примера посмотрим оценки. Использовать будем не классический ящик, а Boxenplot.

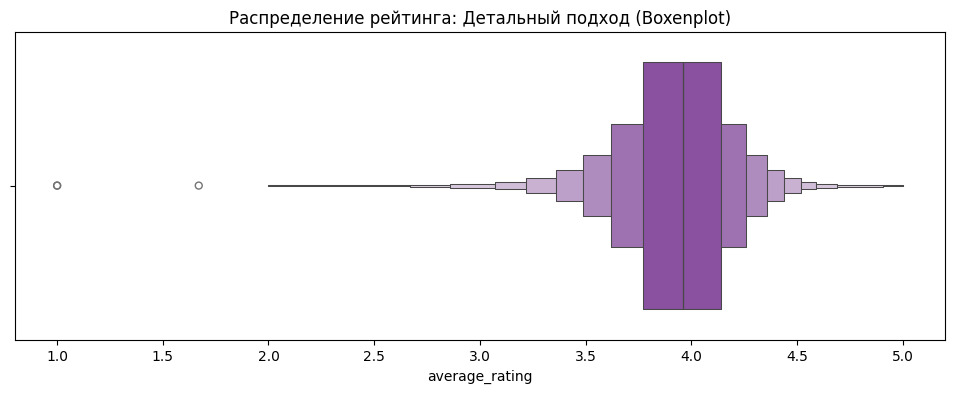
Центральный прямоугольник на графике показывает 50% данных. Это означает, что 50% оценок находится в диапазоне от 3,7 до 4,2. Линия, которая делит этот прямоугольник — медиана. Каждые последующие прямоугольники берутся попарно. Данные за пределами «усов» — выбросы.

Отфильтровать выбросы можно и без графиков. Сделать это можно с помощью критерия Тьюки.

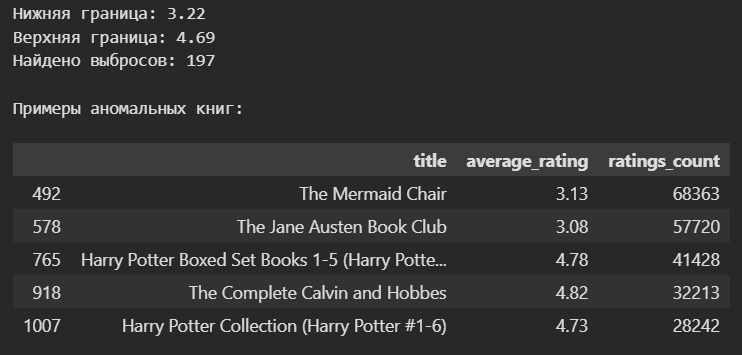
Однако часто не рекомендуют удалять данные, даже если они кажутся выбросами. Поэтому лучше попытаемся превратить нашу таблицу в историю.

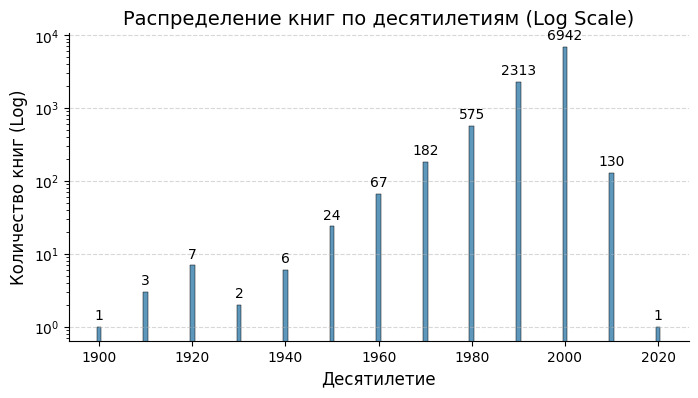
Мы видим, что основная масса книг приходится на 90-е и 00-е. Скорее всего, это связано с особенностями сборки данных. Кроме того, сайт заработал с 2007, поэтому на оценки с этого момента влиял маркетинг непосредственно. Старые же книги оценивались более объективно.

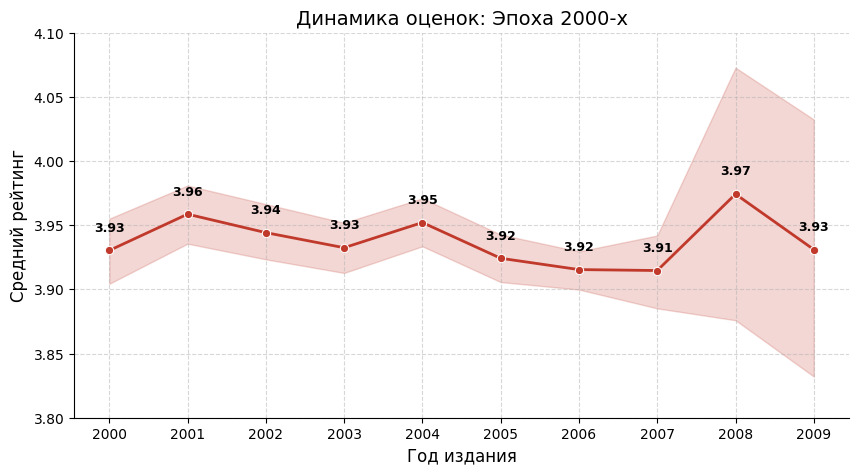
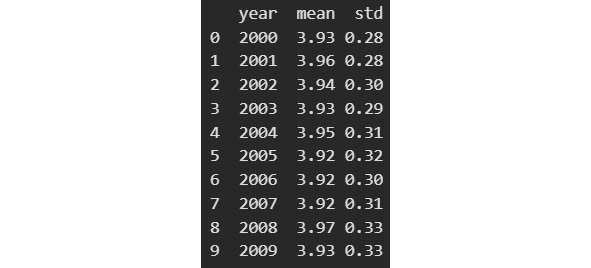
Мы взяли 2000-е, потому что для этого периода у нас достаточно много данных. Видим, что оценки достаточно стабильны. Даже рост до средней оценки в 3,97 в 2008 был чуть ослаблен стандартным отклонением в 0,33.

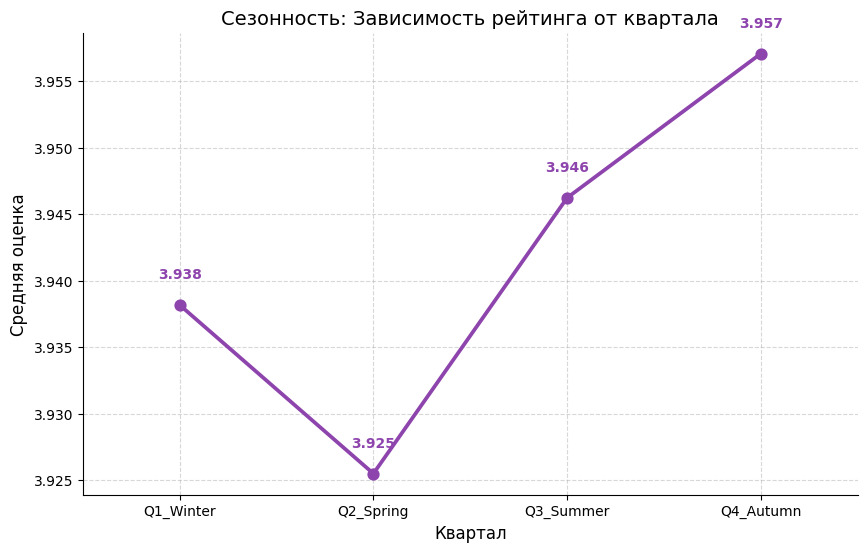
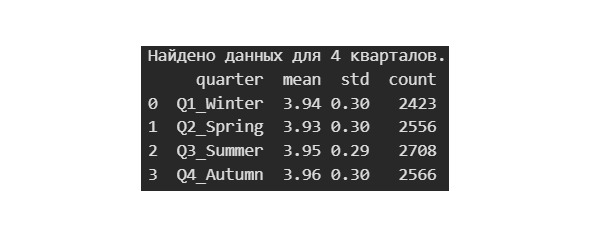
На этом графике мы видим, что максимальную оценку получают книги, выходящие в 4 квартале. А вот книгам зимним и весенним везет уже не так.

После визуализации мы можем приступить к проверке статистических гипотез.

Гипотезы выдвигаются либо о типе распределения, либо о параметрах известного распределения.

Гипотезы делят на нулевую (основную) и конкурирующую (альтернативную). Если можно принять нулевую гипотезу, то необходимо отвергнуть альтернативную. Если же принять нулевую гипотезу нельзя, то необходимо принять альтернативную. Пример: если нулевая гипотеза утверждает, что математическое ожидание равно 10, то альтернативная гипотеза будет утверждать, что математическое значение не равно 10.

Нулевая гипотеза может быть либо истинной, либо ложной. Независимо от этого, можно угадать истинность или угадать ложность гипотезы, или не угадать ни того, ни другого. С учетом этого возможные ошибки делят на два вида: 1) ошибка первого рода возникает, если отвергнута истинная гипотеза. Например, если гипотеза, что математическое ожидание равно 10 является истинной, но пришлось ее отвергнуть, то возникает ошибка первого рода; 2) ошибка второго рода возникает, если принята неправильная гипотеза. Например, если гипотеза, что математическое ожидание равно 10 является ложной, но пришлось ее принять, то возникает ошибка второго рода.

Есть вероятность совершить ошибку первого рода (отвергнуть истинную гипотезу). Такую вероятность называют уровнем значимости. Например, если уровень значимости 0,05, то это означает, что в 5 случаях из 100 можно допустить эту ошибку.

Итак, есть нулевая гипотеза. Возникает вопрос, а как ее проверить? То есть как узнать, что это гипотеза истинная, или узнать, что гипотеза ложная?

Чтобы проверить нулевую гипотезу, нужно выполнить несколько шагов:

1) подобрать специальную случайную величину, распределение которой точно или примерно известно. Эта величина может быть обозначена как U или Z при нормальном распределении, F — при распределении по Фишеру-Снедекора и т. п. Эту величину называют статистическим критерием; 2) на основании имеющихся данных рассчитать те значения, которые входят в специальную случайную величину. Так получают частное (наблюдаемое) значение критерия.

Вот это на примере. Предположим, что мы хотим сравнить дисперсии двух категорий книг — книги в 90-е, и книги в 00-е. Наша гипотеза будет состоять в том, что в 00-е, из-за интернета, разброс оценок увеличился.

Итак, мы считаем дисперсию оценок книг 90-х и дисперсию книг 00-х. У каждой группы есть свое количество книг, такое количество называется степенями свободы. У книг 90-х степень свободы 2463, у книг нулевых степень свободы 7545. Это значит, что всего книг 90-х 2463, а книг 00-х — 7545.

Для книг 90-х дисперсия будет 0.0809, а для книг 00-х — 0.0899. Если бы дисперсии были равны, то деление дало бы 1. Если значение не равно 1, то надо определить случайно это или нет. Если неравенство 1 является случайным, тогда на самом деле деление должно бы давать 1, но из-за каких-то случайных факторов дало другое значение. В этом случае мы принимаем гипотезу, что значение равно 1, то есть дисперсии равны. Посмотрим, так ли это.

Делим большую дисперсию на меньшую. Получаем 1,11, это называется F-статистикой. Теперь мы задаемся вопросом: если есть две степени свободы — 2463 и 7454, то с вероятностью в 95% каким должно быть значение F–статистики? По специальным таблицам находим, что такое значение составляет 1,09. То есть эталонное значение сильно отличается от полученного. Значит невероятно получить соотношение в 1,11 на наших данных. Поэтому гипотеза отвергается.

Мы использовали вероятность в 95%. Отсекать значения можно слева и справа. Посмотрите на рисунок. Тот уровень, который мы отсекам, называется p-value.

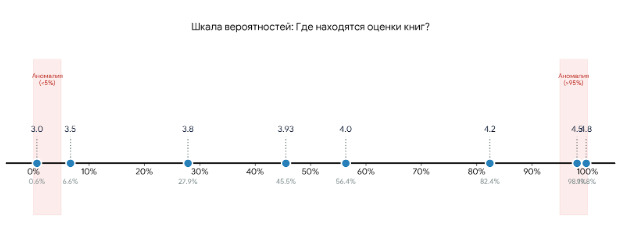
Важно также помнить, что проверка статистических гипотез не доказывает гипотезы. Одного доказательства еще недостаточно для принятия гипотезы. Однако достаточно одного противоречащего гипотезе факта, чтобы ее отвергнуть. Поэтому проверяют гипотезу на возможность принятия несколькими способами, а для отрицания гипотезы хватит и одного.

Дополнительно надо учитывать, что тесты могут быть параметрическими и непараметрическими. Параметрические тесты основаны на известных свойствах распределений. Непараметрические не учитывают свойства распределений. В случае непараметрических тестов метрики распределения определяются с помощью многократного повторения теста.

Также все тесты можно разделить на: применимые только к количественным признакам, применимые только к категориальным признакам, применимые как к количественным, так и категориальным признакам.

Еще одно деление: одни тесты говорят только о наличии связи (отсутствии связи) между признаками, другие тесты также показывают силу этой связи.

Теперь мы проведем тестирования нашего распределения оценок на нормальное распределение.

Базовая проверка на нормальное распределение может быть проведена с помощью критериев асимметрии и эксцесса. У нормального распределения оба значения должны быть равны нулю.

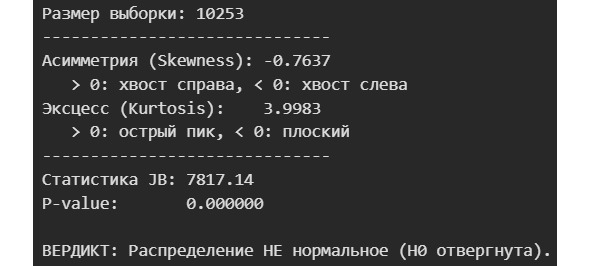
Таким же образом можно тестировать все другие известные распределения, чтобы определить, какое лучше подходит для наших данных. В результате лучшим оказывается бета-тестирование.

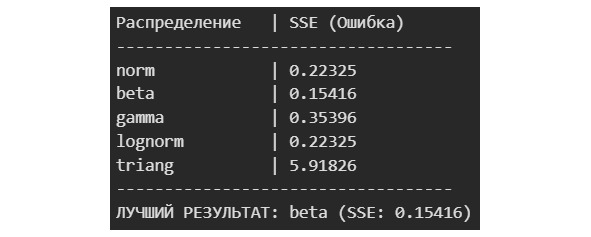
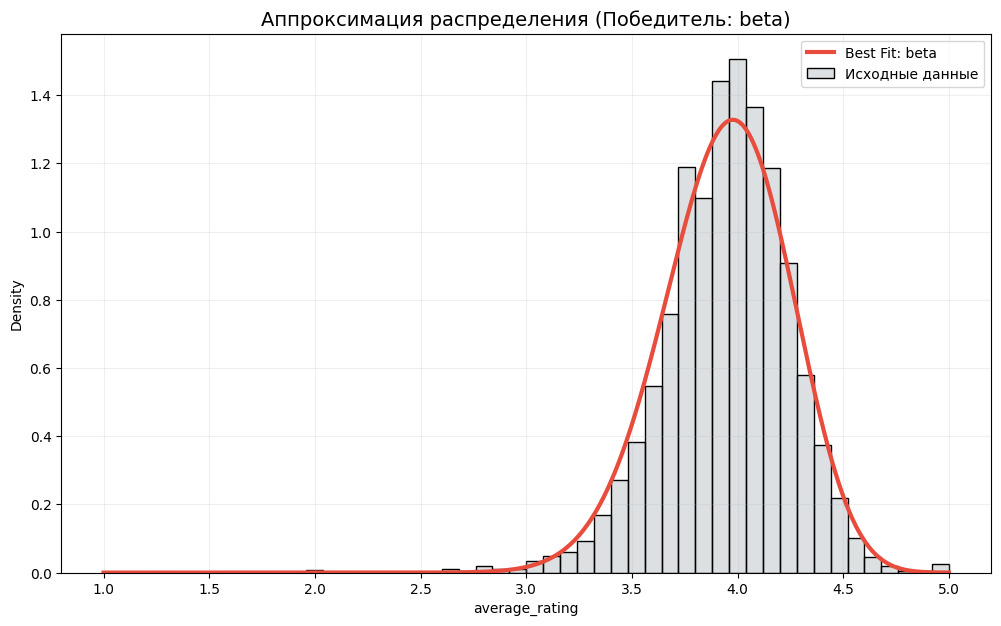
Отличие бета-распределения от обычных в том, что оно работает для данных, которые находятся в определенных границах. У нас это оценки от 1 до 5.

Теперь мы перейдем к поиску корреляций, найденное распределение нам в этом поможет. Если для нормального распределения применяется корреляция Пирсона, то на нашем распределении нужно использовать корреляцию Спирмена.

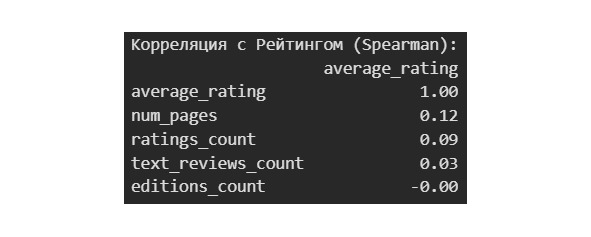
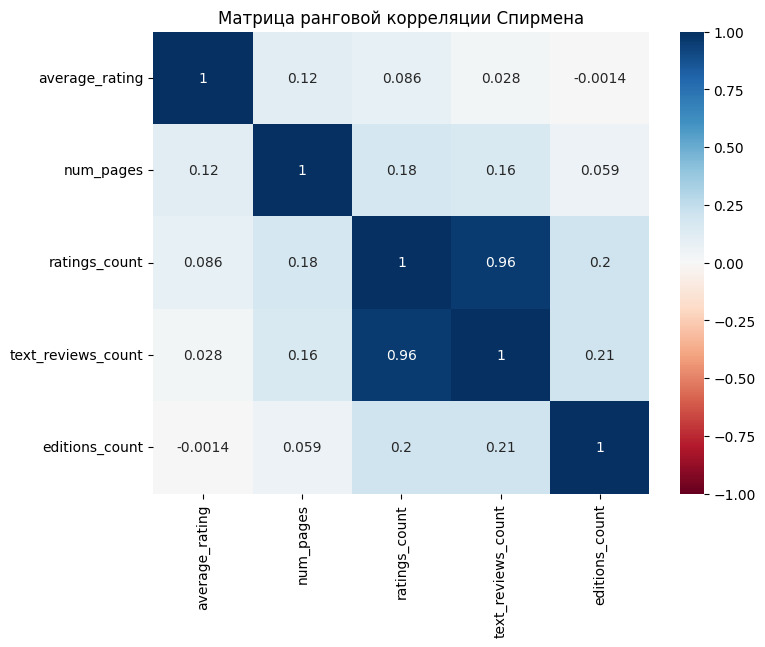
Мы видим, что средняя оценка связана с количеством страниц, но не сильно.

Теперь мы перейдем к дисперсионному анализу.

У нас есть изучаемый нами признак — распределение оценок. Этот признак можно разбить на группы. Например, если взять признак выхода книг по кварталам, то можно все оценки разбить на группы. Одна группа — это оценки книг, которые выходили во 2 квартале, еще одна — оценки книг, которые выходили в 3 квартале и т. п. Среди всех оценок книг есть дисперсия, разброс, но и в группах есть разброс. Например, разброс среди всех оценок будет 1, а разброс внутри оценок книг, вышедших во втором квартале, разброс будет 1,2. Означает ли это, что выход книг во втором квартале действительно влияет на оценку книги? Ответом на этот вопрос и занимается дисперсионный анализ.

Итак, вот какие предположения: есть количественный нормально распределенный признак X; на этот признак воздействует фактор F; фактор F имеет p постоянных уровней; число наблюдений (испытаний) на каждом уровне одинаково и равно q.

Понять это можно по такой таблице.

Теперь посмотрим формулы для расчета.

Обозначения:

Основные уравнения (Суммы квадратов)

1. Общая вариация

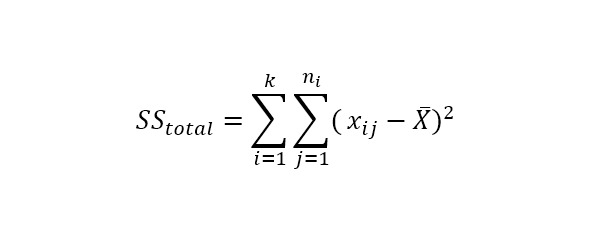
2. Межгрупповая вариация

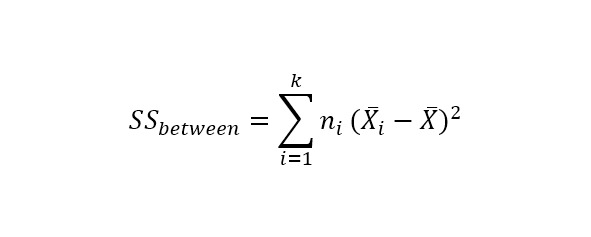
3. Внутригрупповая вариация

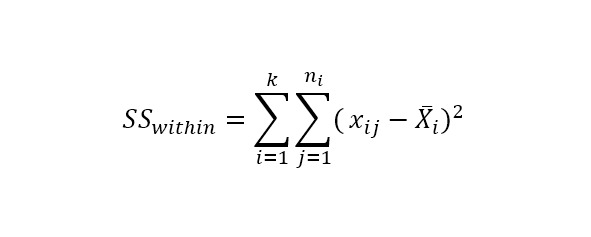
Проверка: