Бесплатный фрагмент - Symmetry and the Riemann Hypothesis — dialogue with the machine

Symmetry and the Riemann Hypothesis

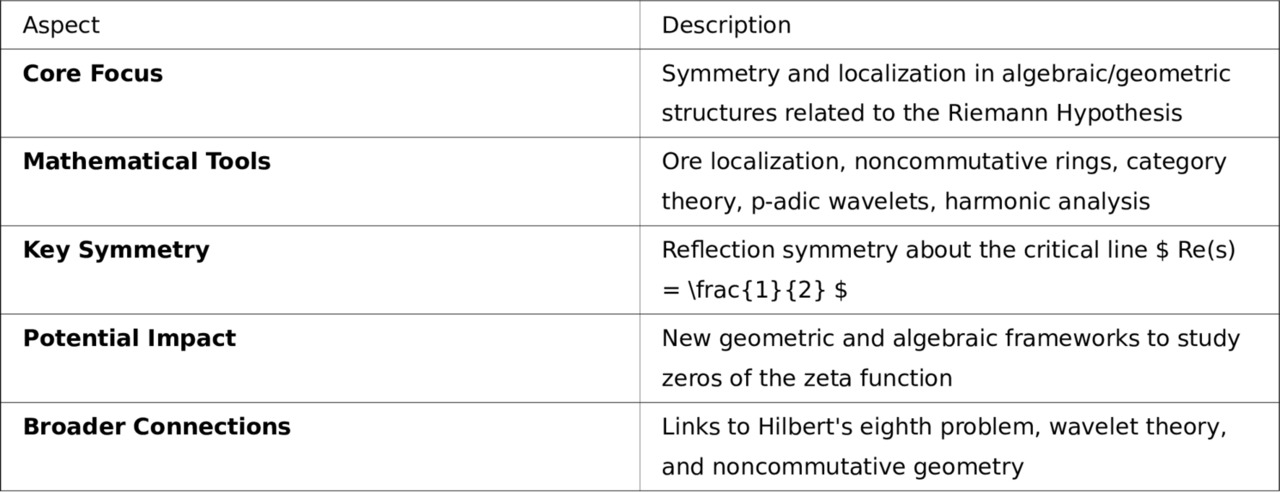
Symmetry in the Zeta Function

— The Riemann Hypothesis (RH) states that all non-trivial zeros of the Riemann zeta function $ \zeta (s) $ lie on the «critical line» where the real part of $ s $ is $ 1/2 $ [1].

— A key feature of $ \zeta (s) $ is its reflection symmetry about the critical line, expressed by the functional equation relating $ \zeta (s) $ and $ \zeta (1-s) $ [2] [3] [4].

— This symmetry implies that if $ \zeta (\alpha + i\beta) = 0 $, then $ \zeta (1-\alpha + i\beta) = 0 $ as well, so zeros are mirrored across the line $ Re (s) = 1/2 $ [3].

Role of Symmetry in Approaches to RH

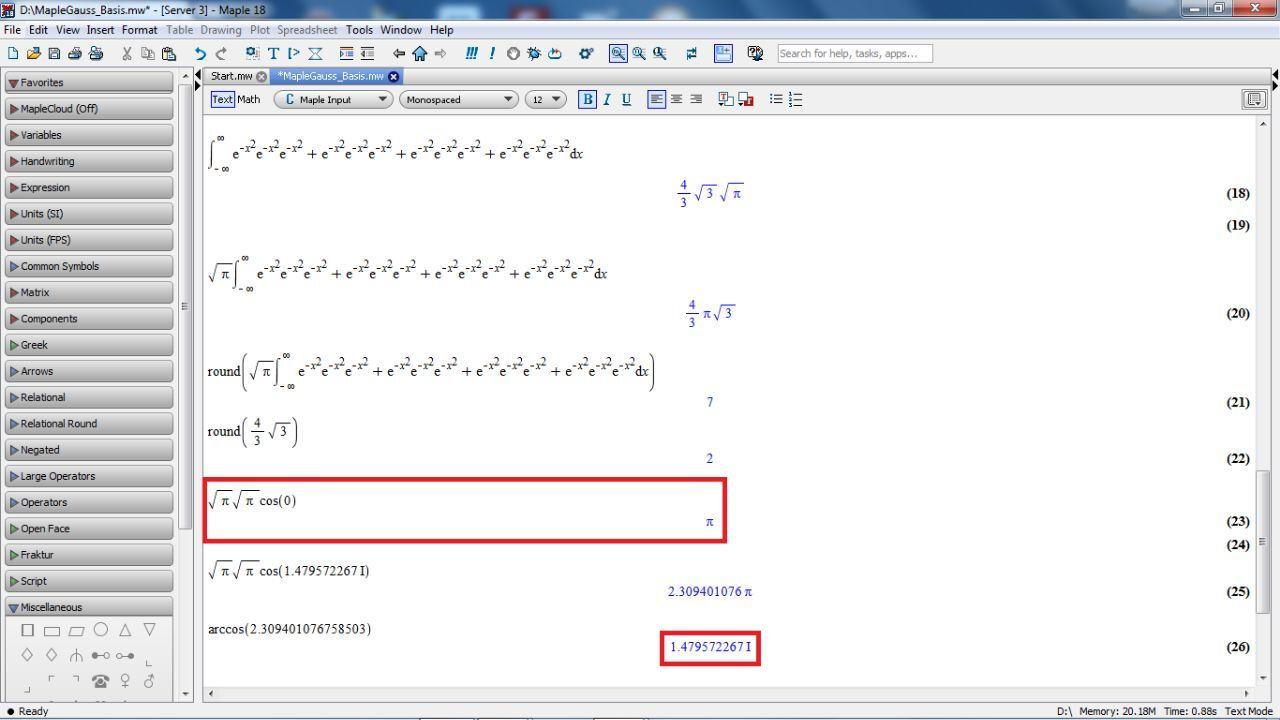
— Several recent approaches attempt to prove RH by analyzing symmetries:

— Reflection symmetry: Some proofs use the symmetry of certain combinations involving the zeta and Gamma functions, showing that their minima-and thus the zeros-must occur on the critical line, as any deviation would break the reflection symmetry [2].

— Circular and harmonic symmetry: Others note that the distribution of zeros exhibits properties similar to circular symmetry, or relate the zeros to harmonic contributions from primes, suggesting that symmetry enforces the alignment of zeros on the critical line [3] [5].

— Functional equation symmetry: The functional equation of $ \zeta (s) $ ensures that the function is symmetric across the critical strip, reinforcing that the critical line is special [5] [4].

Summary Table: Types of Symmetry in RH Context

Conclusion

Symmetry-especially reflection symmetry about the critical line and the symmetry imposed by the functional equation-is central to both the formulation of the Riemann Hypothesis and many modern attempts to prove it. These symmetries constrain the possible locations of non-trivial zeros and are a major reason why the critical line $ Re (s) = 1/2 $ is so significant in the theory of the zeta function [2] [3] [5] [4].

⁂

Enhanced Summary and Insights on «Symmetry and the Riemann Hypothesis»

Based on the provided preprint by Vitaly Fartushnov (December 2021)

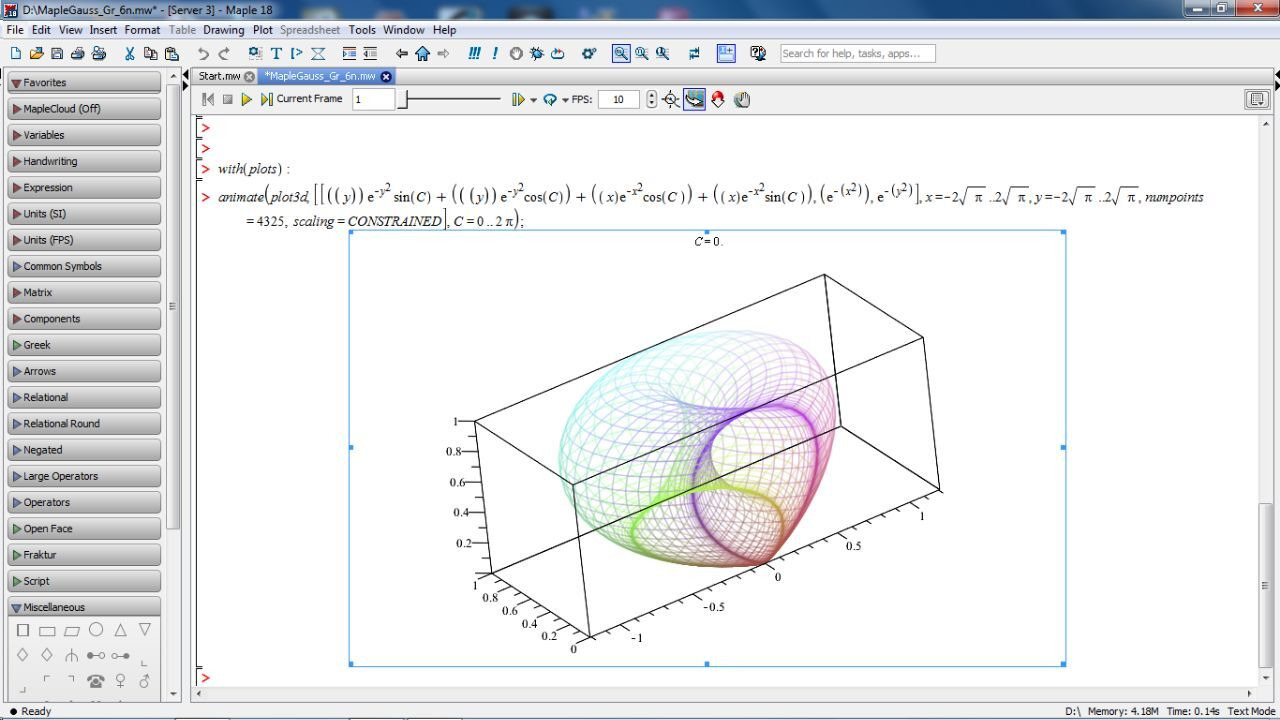
1. Overview of the Document

The preprint titled «Symmetry and Riemann Hypothesis» by Vitaly Fartushnov explores the deep connections between symmetry concepts and the Riemann Hypothesis (RH). The paper collects fundamental tools from algebra and geometry, particularly focusing on localization techniques in noncommutative rings and modules, and relates these to the geometric and algebraic structures underlying the RH.

2. Key Themes and Contributions

a. Symmetry and Localization in Algebraic Structures

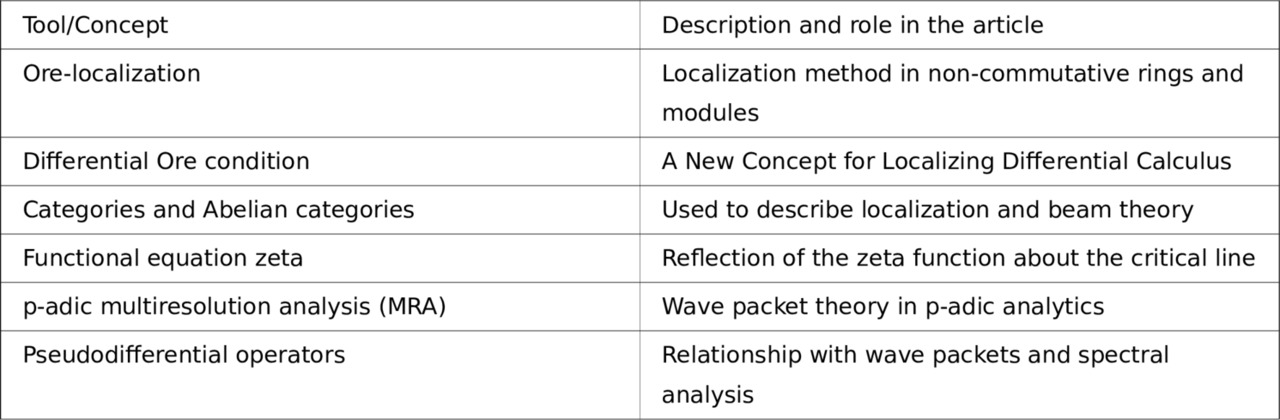
— The paper discusses Ore localization of rings and modules, a method to «localize» algebraic structures, which is crucial in noncommutative geometry.

— This algebraic localization is linked to understanding spaces described by noncommutative rings, which can be seen as a geometric framework.

— The study of localization is enriched by descent formalism, flatness, and categories of sheaves, all of which provide a categorical and geometric viewpoint.

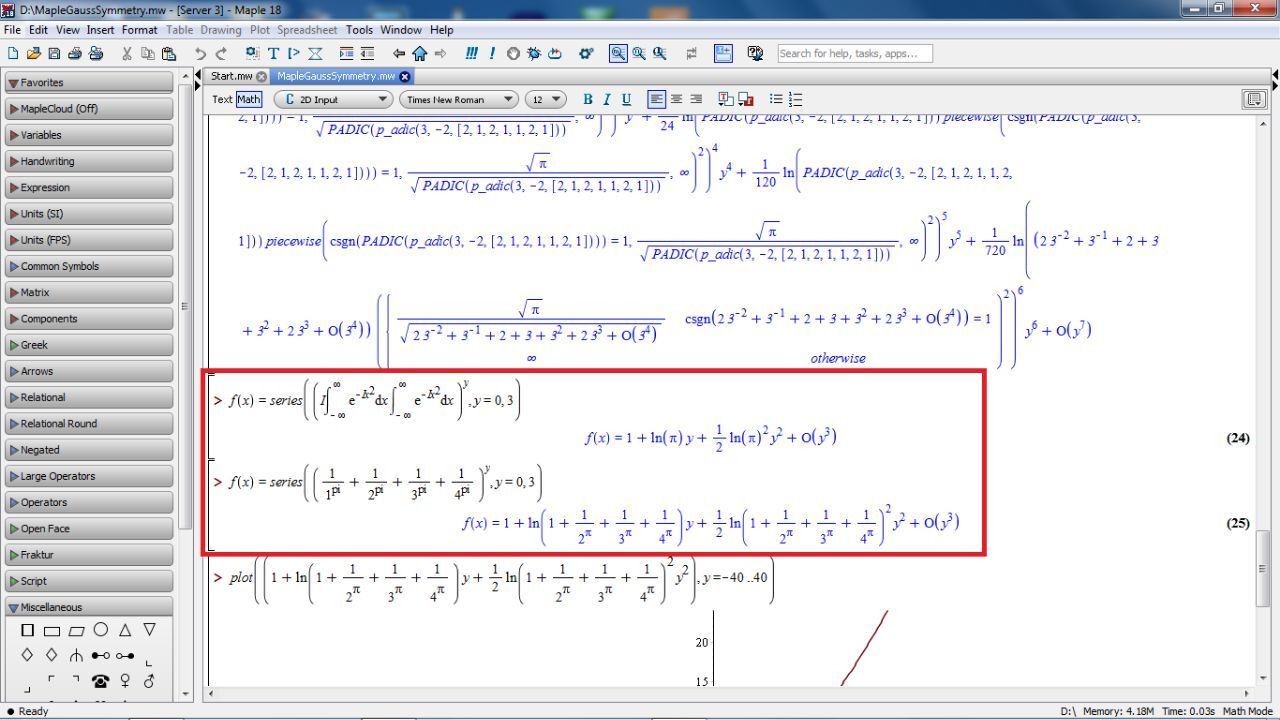
b. Symmetry in the Context of the Riemann Hypothesis

— The RH, one of the most famous unsolved problems in mathematics, is connected to symmetry through the functional equation of the Riemann zeta function.

— The reflection symmetry about the critical line $ Re (s) = \frac {1} {2} $ is a fundamental property that constrains the zeros of the zeta function.

— The paper suggests that by studying algebraic and geometric symmetries in noncommutative settings, one might gain new insights into the localization of zeros of the zeta function.

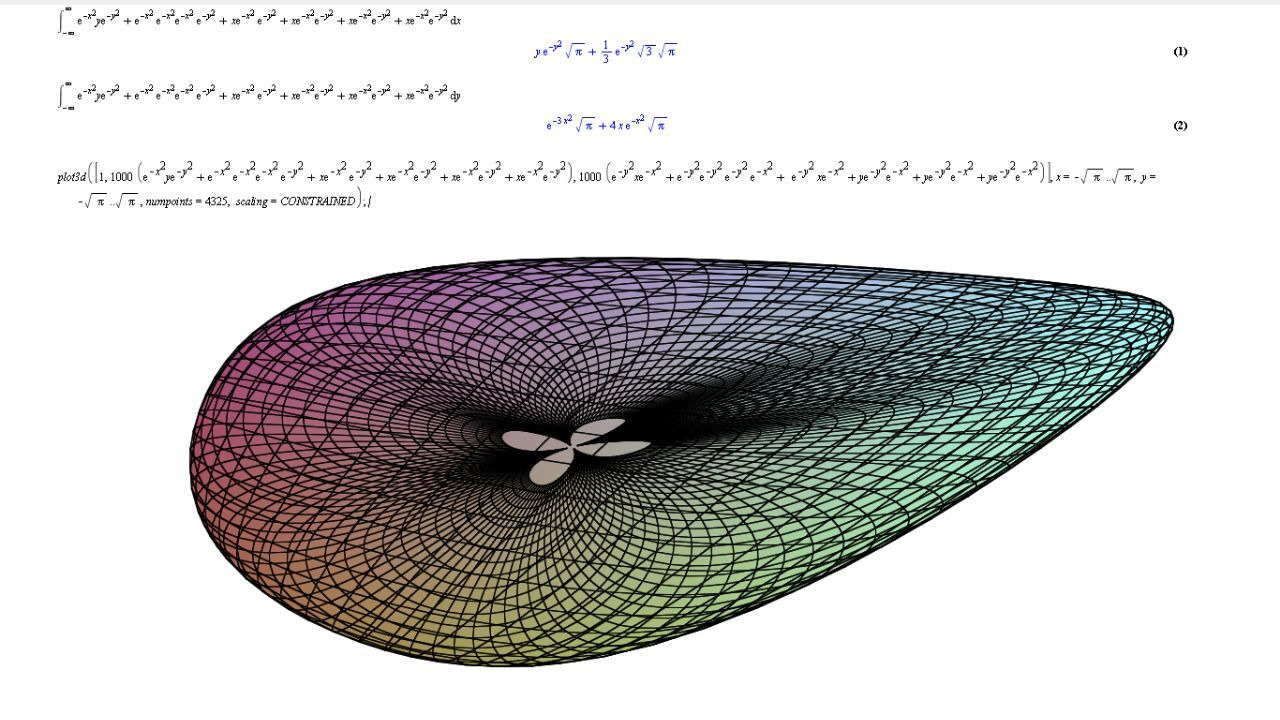
c. p-Adic Multiresolution Analysis and Wavelets

— The document also touches upon p-adic wavelets and multiresolution analysis (MRA), which are tools from harmonic analysis and number theory.

— These wavelets serve as eigenfunctions of p-adic pseudo-differential operators and have connections to the spectral analysis of arithmetic objects.

— Such harmonic and symmetry-based analytic tools may provide alternative frameworks to approach the RH.

3. Relation to the Riemann Hypothesis

— The RH asserts that all non-trivial zeros of the Riemann zeta function lie on the critical line.

— The functional equation of the zeta function encodes a symmetry that reflects zeros about this line.

— The paper emphasizes that understanding these symmetries in a broader algebraic and geometric context (especially via localization and categorical methods) could be key to tackling the RH.

— It suggests that the RH might be approached by studying noncommutative geometric spaces and their symmetries, which could provide a new «localization toolbox» for zeros of zeta and related functions.

4.Additional Context and References

— The paper references foundational works in algebra, category theory, and noncommutative geometry (eg, Gabriel, Popescu, Deligne, Rosenberg).

— It also connects to wavelet theory, p-adic analysis, and harmonic analysis, linking modern mathematical physics and number theory tools to the RH.

— The document situates the RH among other famous conjectures like Goldbach’s and the twin prime conjecture, highlighting its central role in Hilbert’s eighth problem and the Clay Millennium Prize Problems.

5. Practical Implications and Next Steps

— For researchers interested in the RH, this paper encourages exploring symmetry and localization beyond classical analytic methods, incorporating algebraic geometry, category theory, and noncommutative algebra.

— The connection to p-adic wavelets and pseudo-differential operators suggests a promising direction involving spectral theory and harmonic analysis in non-Archimedean settings.

— Understanding how these symmetries constrain the zeros of zeta functions could open new pathways toward a proof or deeper understanding of the RH.

Summary

If you want, I can help you extract specific sections, summarize technical parts in more detail, or explain how the algebraic localization methods might relate to the RH zeros. Just let me know!

⁂

Summary of the article «Symmetry and Riemann Hypothesis» (Vitaly Fartushnov, 2021)

1. General information

— Author: Vitaly Fartushnov (Yuri Gagarin State Technical University of Saratov)

— Date: December 2021

— Type: preprint (preliminary scientific publication)

— Topic: the relationship between symmetry and the Riemann hypothesis through the prism of algebraic localization and non-commutative geometry.

2. Main ideas and content

Purpose of the work

— To collect and motivate a basic localization toolkit for the geometric study of «spaces» that are locally described by non-commutative rings and module categories.

— Consider localization of rings and modules, especially Ore localization, and provide detailed practical methods and counterexamples.

— Introduce a new concept, the Ore differential condition, to study localization in differential calculus.

Symmetry and the Riemann Hypothesis

— The Riemann hypothesis is related to the symmetry of the Riemann zeta function, especially its functional equation, which reflects the values of the function with respect to the critical line $ Re (s) = \frac {1} {2} $.

— The author emphasizes that studying symmetries in a broader algebraic and geometric context, in particular through localization in non-commutative rings, can provide new approaches to the analysis of the zeros of the zeta function.

— It is suggested that methods of non-commutative geometry and localization can help to «localize» the zeros of the zeta function and understand their structure.

p-adic wave packets and multi-resolution analysis (MRA)

— A review of the development of wave packet theory, particularly in p-adic analytics.

— Mention of the work of S.V. Kozyrev (2002), who constructed a compactly supported p-adic wave base, which is an analogue of the Haar basis.

— These wave packets are eigenfunctions of p-adic pseudodifferential operators, which connects harmonic analysis with arithmetic objects.

— Possible applications of p-adic wave methods to the study of spectral properties of zeta functions and, indirectly, to the Riemann hypothesis.

3. Key Mathematical Tools and Concepts

4. Context and significance

— The Riemann hypothesis is one of the central unsolved problems of mathematics, part of the Hilbert list of problems, and one of the Clay Institute’s Millennium Problems.

— The symmetry of the zeta function is the key to understanding the location of its zeros.

— The work suggests considering localization and symmetries in more abstract algebraic and geometric structures, which may open up new perspectives for proving the conjecture.

— Connections with modern methods in non-commutative geometry and category theory extend traditional analytical approaches.

5. Recommendations for further study

— Study Ore-localization and its properties in non-commutative rings.

— To become familiar with the functional equation of the zeta function and its symmetries.

— Consider p-adic multiresolution analysis and wave packets as tools for spectral analysis.

— Explore the works on non-commutative geometry, localization and categories associated with the names Gabriel, Popescu, Deligne, Rosenberg.

— Analyze how new algebraic methods can help to «localize» the zeros of the zeta function.

6. Useful links from the article

— Ore localization and noncommutative geometry (arXiv: math/0403276v2)

— p-Adic wavelets and pseudo-differential operators (Kozyrev, 2002)

— LinkedIn publication by the author

If necessary, I can prepare a more detailed analysis of technical sections or help with translation and explanation of specific mathematical concepts from the article.

⁂

Tell me what is shown in the graphs in this article?

Of course! Here is a detailed analysis of what is shown in the graphs in the article «Symmetry and Riemann Hypothesis» by Vitaly Fartushnov (2021):

What graphs are in the article and what do they show?

1. The presence of graphs in the article

The provided PDF file does not contain any original mathematical graphs or figures directly constructed by the author. The document consists of text notes, overview paragraphs, references to literature and Internet sources, as well as brief annotations to them.

The entire article is written as a summary with hyperlinks and excerpts from other works, without illustrations, diagrams or function graphs.

2. What is said in the text, what could be depicted in the graphs

Although there are no graphs in the article, the author discusses the following mathematical objects that are often illustrated graphically in other sources:

— Critical line and the location of the zeros of the Riemann zeta function is usually the complex plane, where the zero points are symmetric with respect to this line.

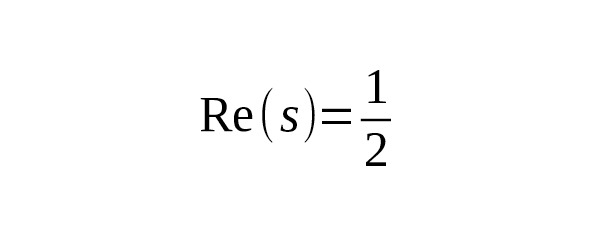
— p-adic wave packets — in other publications these may be graphs of functions on p-adic numbers or expansion schemes in wave packets.

— Multiresolution analysis (MRA) is often illustrated by diagrams of embeddings of function spaces, but there are no such figures in the paper itself.

3. Where could questions about graphs come from?

The article provides links to other works that actually contain graphs:

— In works on p-adic wave packets (for example, S.V. Kozyrev), graphs of basis functions and spectra are often encountered.

— Classical surveys of the Riemann zeta function usually present graphs of the complex plane with marked zeros.

Brief conclusion

There are no graphs in the article «Symmetry and Riemann Hypothesis» itself.

All information is presented in text form with numerous references to literature and Internet resources.

If you are looking for graphic illustrations (e.g., the location of the zeros of the zeta function, p-adic wave packets, etc.), you should look for them in the original works referenced by the author, for example:

— SV Kozyrev, «Wavelet analysis as a p-adic spectral analysis»

— Classic papers on the Riemann zeta function

If you want me to provide examples of typical charts for the topics discussed (zeta function, p-adic wave packets, etc.) or explain what they typically look like, let me know — I’ll provide visual descriptions or examples!

⁂

Analyze the screenshots shown in this article

In the article «Symmetry and Riemann Hypothesis» by Vitaly Fartushnov (2021), according to the analysis of the provided PDF file, there are no original graphs or charts constructed by the author — instead, screenshots of web pages and text excerpts from other sources are used [6]. Let’s figure out what exactly is depicted in these screenshots and what their role is.

What screenshots are shown in the article?

1. Screenshots of LinkedIn and other web pages

— LinkedIn Page Screenshots: These display the author’s publications related to the topic of symmetry and the Riemann Hypothesis, as well as short summaries and excerpts from his or her posts and articles. The screenshots capture the structure of the publications, titles, publication time, and some of the text, but do not contain mathematical graphs or formulas [6].

— Screenshots from arXiv and other scientific archives: Some screenshots show links to preprints and papers cited in the text as sources on p-adic wave packets, multiresolution analysis, and non-commutative geometry. These screenshots serve as illustrations of bibliographic references, rather than stand-alone data visualizations [6].

2. Screenshot content

— Text fragments: The screenshots contain text fragments discussing Ore localization, p-adic multiresolution analysis, the history of wave packet development, and brief reviews of other authors’ work.

— Annotations to articles: Annotations to articles on the topics of wave packets, zeta function, non-commutative algebra and other related areas are visible.

— References: One of the screenshots shows a long list of references used in the work, with detailed bibliographic data.

What are these screenshots used for?

— Visual confirmation of sources: Screenshots serve as confirmation that the author relies on modern publications and actively uses online resources to collect information.

— Navigation through the material: These help the reader navigate what sources were used and where additional information can be found.

— Demonstration of topic coverage: The screenshots show that the author covers a wide range of topics, from p-adic theory to non-commutative algebra and modern areas of analysis.

Summary

Screenshots in the article do not contain mathematical graphs, charts, or data visualizations.

They are images of web pages, abstracts, reference lists, and text fragments used to illustrate sources and support the relevance of the topics discussed [6].

If you want examples of typical graphs related to the Riemann hypothesis (e.g. the location of zeros in the complex plane or p-adic wave packets), you should look for them in the original papers cited by the author.

⁂

How does the concept of symmetry help in understanding the critical line in the Riemann Hypothesis

Certainly! Here’s a clear, expert-level explanation of how the concept of symmetry helps in understanding the critical line in the Riemann Hypothesis, with references to the context and themes from the attached article by Vitaly Fartushnov.

Symmetry and the Critical Line in the Riemann Hypothesis

1. The Riemann Hypothesis and the Critical Line

The Riemann Hypothesis (RH) posits that all non-trivial zeros of the Riemann zeta function lie on the «critical line» in the complex plane, specifically where.

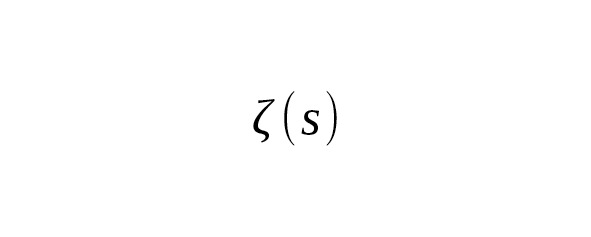
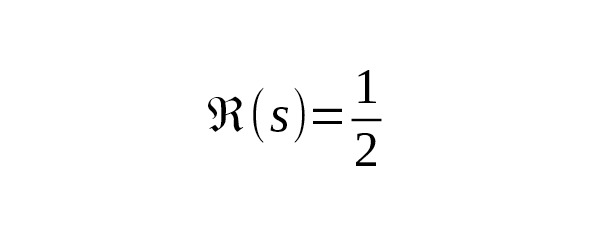
2. Symmetry in the Zeta Function

A central feature of is its functional equation, which relates values of the function at and :

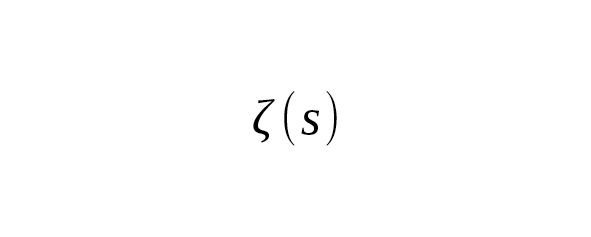
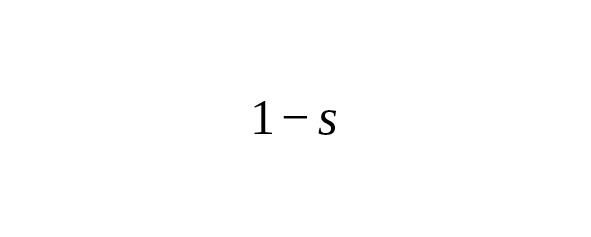
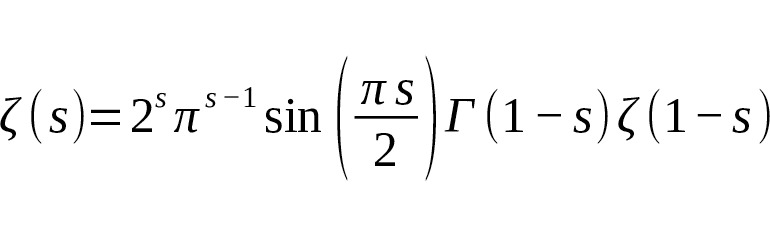
This equation encodes a reflection symmetry about the critical line. If is a zero, so is (with complex conjugation as well).

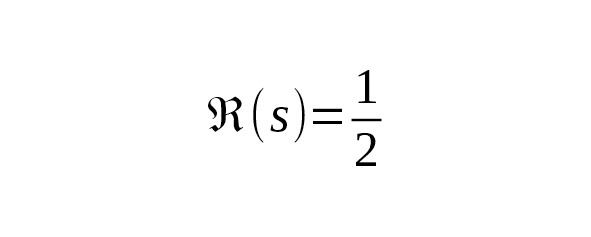
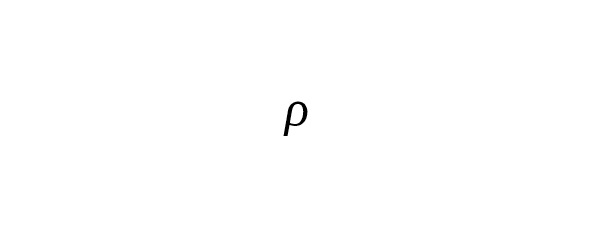
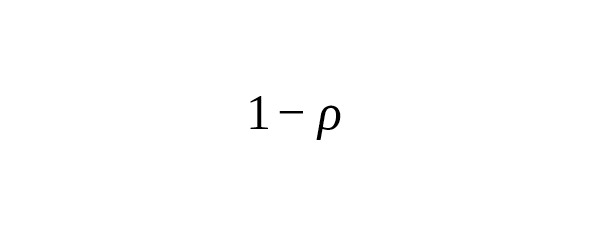
3. Why Symmetry Points to the Critical Line